四川省乐山市2022年中考数学模拟试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果向东走3米记为+3米，那么向西走6米记作（）．

A、+3米 B、-3米 C、-6米 D、+6米

查看试题解析
2. 班级共有40名学生，在一次体育抽测中有8人不合格，那么不合格人数的频率为（）

A、0.2 B、0.25 C、0.55 D、0.8

查看试题解析
3. 某次列车平均提速v千米/每小时，用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度是（）km/h．

A、 $\frac{s v}{50}$ B、 $\frac{50 v}{s}$ C、 $\frac{50}{s v}$ D、 $\frac{v}{50 s}$

查看试题解析
4. 将一副直角三角板如图放置，使两直角重合，则 $∠ A F E =$ （）度

A、145 B、155 C、165 D、175

查看试题解析
5. 若点P（2，1）在过原点的一条直线上，则这条直线所对应的函数表达式为（）

A、 $y = - 2 x$ B、 $y = \frac{1}{2} x$ C、 $y = 2 x - 1$ D、 $y = 1 - 2 x$

查看试题解析
6. 如图是由几个小正方体组成的一个几何体，这个几何体从正面看到的平面图形是（）

A、 B、 C、 D、

查看试题解析
7. 七巧板是我们民间流传最广的一种古典智力玩具，由正方形分割而成（如图），图中6号部分的面积是正方形面积的（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{1}{8}$ D、 $\frac{1}{16}$

查看试题解析
8. 如图，在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ， E为BC边的中点，M为对角线BD上的一个动点．则下列线段的长等于 $A M + \frac{1}{2} B M$ 最小值的是（）

A、AD B、AE C、BD D、BE

查看试题解析
9. 如图，点P在抛物线y＝x²﹣3x+1上运动，若以P为圆心的圆与x轴、y轴都相切，则符合上述条件的所有的点P共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如果一个矩形的周长为12，面积为4，设它的长为x，宽为y，则x+y＝6，xy＝4．满足要求的（x，y）是直角坐标系内双曲线y＝ $\frac{4}{x}$ 与直线y＝﹣x+6在第一象限内的交点坐标，如图所示，如果把周长为12、面积为4的矩形，周长和面积分别减半（简称为减半矩形），以下结论正确的是（）

A、不存在这样的减半矩形 B、存在无数个这样的减半矩形 C、减半矩形的边长为3+ $\sqrt{7}$ 和3﹣ $\sqrt{7}$ D、减半矩形的边长为1和2

查看试题解析

二、填空题

11. 零指数幂a⁰＝1（a≠0）的意义，即任何不等于0的数的0次幂都等于1；负整数指数幂a^﹣p＝（a≠0，p为数），要特别注意a≠0的附加条件．用科学记数法表示一些绝对值较小的数，即将它们表示成a×10^﹣n的形式，其中n是数，1≤|a|＜10．引进了零指数幂和负整数指数幂后，指数的范围就从正整数扩大到了全体整数，我们以前学习过的各种幂的性质在整数范围内仍然成立．

查看试题解析
12. 因式分解：（a﹣b）²﹣1＝．

查看试题解析
13. 小华和小苗两人练习射击的成绩如图所示，小华和小苗两人成绩的方差分别为 $S_{1}^{2}$ ， $S_{2}^{2}$ ，根据图中的信息判断两人方差的大小关系为 $S_{1}^{2}$ $S_{2}^{2}$ （填“＞”，“＜”或“=”）．

查看试题解析
14. 高新一中初中校区九年级（一）班课外活动小组为了测得学校旗杆的高度，他们在离旗杆6米的A处，用高为1.5米的仪器测得旗杆顶部B处的仰角为60°，如图所示，则旗杆的高度为米．（结果保留根号）

查看试题解析
15. 在△ABC 中，∠A=30°，∠B=90°，AC=8，点 D 在边 AB，且 BD= $\sqrt{3}$ ，点 P 是△ABC 边上的一个动点，若 AP=2PD 时，则 PD的长是．

查看试题解析
16. 如图，在平面直角坐标系中，点A的坐标为(3，4)，那么sin $α$ 的值是

查看试题解析

三、解答题

17. 当x取何值时，代数式2（x＋5）的值小于代数式13＋5x的值？

查看试题解析
18. 等腰Rt△ABC与等腰Rt△ADE，AB＝BC，AD＝DE，∠ABC＝∠ADE＝90°，连接CE，取CE中点G，连接BG，DG，探索BG，DG的关系．

查看试题解析
19. 下面是某同学在完成作业本（2） $P 43$ 第5题第（2）小题的过程．
$m + 1 - \frac{m^{2}}{m - 1} = (m + 1) (m - 1) - m^{2}$ ……①

$= m^{2} - 1 - m^{2}$ ……②

$= - 1$ ……③

上面的解题过程 ▲ （填“正确”或“错误”）；如果正确，请写出每一步的依据；如果有错，请写出从第几步开始出错，并写出正确的解题过程．

查看试题解析
20. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示．

(1)、求方程ax²+bx+c＝0的两个根．

(2)、当y＞0时，求x的取值范围．

(3)、当y随着x的增大而减小时，求自变量x的取值范围．

(4)、若方程ax²+bx+c＝k有两个不相等的实数根，求k的取值范围．

查看试题解析

21. 某大学为了解大学生对中国共产党党史知识的学习情况，在大学一年级和二年级举行有关党史知识测试活动，现从一二两个年级中各随机抽取20名学生的测试成绩（满分50分，30分及30分以上为合格：40分及40分以上为优秀）进行整理、描述和分析，给出了下面的部分信息．

大学一年级20名学生的测试成绩为：39，50，39，50，49，30，30，49，49，49，43，43，43，37，37，37，43，43，37，25

大学二年级20名学生的测试成绩条形统计图如下图所示；两个年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如表所示：

年级	平均数	众数	中位数	优秀率
大一	a	b	43	m
大二	39.5	44	c	n

请你根据上面提供的所有信息，解答下列问题：

(1)、上表中a＝ ▲ ， b＝ ▲ ， c＝ ▲ ， m＝ ▲ ， n ▲ ；根据样本统计数据，你认为该大学一、二年级中哪个年级学生掌握党史知识较好？并说明理由（写出一条理由即可）；

(2)、已知该大学一、二年级共1240名学生参加了此次测试活动，通过计算，估计参加此次测试活动成绩合格的学生人数能否超过1000人；

(3)、从样本中测试成绩为满分的一、二年级的学生中随机抽取两名学生，用列举法求两人在同一年级的概率．

查看试题解析

22. 如图，直线y₁＝x+b交x轴于点B，交y轴于点A(0，2)，与反比例函数 $y_{2} = \frac{k}{x}$ 的图象交于C(1，m)，D(n，－1)，连接OC、OD．

(1)、求k的值；

(2)、求 $△$ COD的面积；

(3)、根据图象直接写出y₁＜y₂时，x的取值范围．

查看试题解析
23. 面积一定的梯形，其上底长是下底长的 $\frac{1}{2}$ ，设上底长为xcm，高为ycm，且当x＝5cm，y＝6cm，

(1)、求y与x的函数关系式；

(2)、求当y＝4cm时，下底长多少？

查看试题解析
24. 如图，A为⊙O外一点，AO⊥BC，直径BC＝12，AO＝10， $\overset{⌢}{B D}$ 的长为π，点P是BC上一动点，∠DPM＝90°，点M在⊙O上，且∠DPM在DP的下方．

(1)、当sinA＝ $\frac{3}{5}$ 时，求证：AM是⊙O的切线；

(2)、求AM的最大长度．

查看试题解析
25. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，过A作AD⊥BC交于D，点P为AB边上一点，连接CP，交AD于点E，过A作AF⊥PC分别交PC、BC于F、Q两点；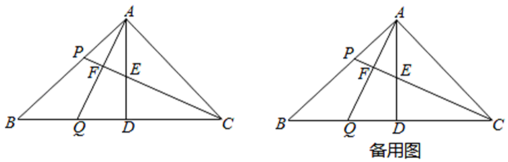

(1)、求证：AE＝BQ；

(2)、若AC＝kAP，求 $\frac{B Q}{A P}$ （用含k的代数式表示）；

(3)、在（2）的条件下，连接BF，若BF＝BD，求k的值．

查看试题解析
26. 已知：如图，抛物线y＝ax²﹣2ax﹣3a交x轴正半轴于点A，负半轴于点B，交y轴于点C，tan∠OBC＝3．

(1)、求a值；

(2)、点P为第一象限抛物线上一点，连接AC、PA、PC，若点P的横坐标为t，△PAC的面积为S，求S与t的函数解析式，（请直接写出自变量t的取值范围）；

(3)、在（2）的条件下，过点P作PD∥y轴交CA延长线于点D，连接PB，交y轴于点E，点Q为第二象限抛物线上一点，连接QE并延长分别交x轴、抛物线于点N、F，连接FD，交x轴于点K，当E为QF的中点且FN＝FK时，求直线DF的解析式．

查看试题解析