四川省泸州市龙马潭区2022年九年级下学期数学一诊模拟考试试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的相反数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 光年是天文学中的距离单位.1光年约是9 500 000 000 000km，用科学记数法可表示为（）

A、950×10¹⁰km B、95×10¹¹km C、9.5×10¹²km D、0.95×10¹³km

查看试题解析
3. 下列计算正确的是（）

A、 $x^{4} + x^{4} = x^{16}$ B、 $(- 2 a)^{2} = - 4 a^{2}$ C、 $x^{7} \div x^{5} = x^{2}$ D、 $m^{2} \cdot m^{3} = m^{6}$

查看试题解析
4. 如图是我国几家银行的标志，其中即是轴对称图形又是中心对称图形的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 把不等式组 ${\begin{array}{l} 2 x + 4 〉 0 \\ x - 3 (x - 2) \geq 4 \end{array}$ 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图是由5个大小相同的正方体组成的几何体，它的俯视图为（）

A、 B、 C、 D、

查看试题解析
7. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围是（）

A、 $k > - 1$ B、 $k > - 1$ 且 $k \neq 0$ C、 $k < 1$ D、 $k < 1$ 且 $k \neq 0$

查看试题解析
8. 如图，在△ABC中，点D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD∶DB＝3∶5，那么CF∶CB等于（）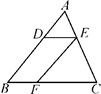

A、5∶8 B、3∶8 C、3∶5 D、2∶5

查看试题解析
9. 已知三角形的三边长分别为a、b、c，求其面积问题，中外数学家曾经进行过深入研究，古希腊的几何学家海伦（Heron，约公元50年）给出求其面积的海伦公式S= $\sqrt{p (p - a) (p - b) (p - c)}$ ，其中p= $\frac{a + b + c}{2}$ ；我国南宋时期数学家秦九韶（约1202-1261）曾提出利用三角形的三边求其面积的秦九韶公式S= $\frac{1}{2} \sqrt{a^{2} b^{2} - (\frac{a^{2} + b^{2} - c^{2}}{2})^{^{2}}}$ ，若一个三角形的三边长分别为2，3，4，则其面积是（）

A、 $\frac{3 \sqrt{15}}{8}$ B、 $\frac{3 \sqrt{15}}{4}$ C、 $\frac{3 \sqrt{15}}{2}$ D、 $\frac{\sqrt{15}}{2}$

查看试题解析
10. 如图，AB是⊙O的直径，弦CD⊥AB于E，∠CDB=30°，⊙O的半径为 $\sqrt{3}$ ，则弦CD的长为（）

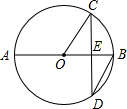A、 $\frac{3}{2} c m$ B、3cm C、 $2 \sqrt{3} c m$ D、9cm

查看试题解析
11.
如图，正方形ABCD的边长为3cm，动点M从点B出发以3cm/s的速度沿着边BC—CD—DA运动，到达点A停止运动，另一动点N同时从点B出发，以1cm/s的速度沿着边BA向点A运动，到达点A停止运动，设点M运动时间为x(s)，△AMN的面积为y（cm²），则y关于x的函数图象是（）

A、 B、 C、 D、

查看试题解析
12. 如图，二次函数y＝ax²+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x₁ ， x₂如，其中﹣1＜x₁＜0，1＜x₂＜2，下列结论：①4a+2b+c＜0；②2a+b＞0；③b²+8a＞4ac；④a＜﹣1．其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $16 m^{3} - m n^{2}$ =

查看试题解析
14. 已知关于x的分式方程 $\frac{k}{x + 1} + \frac{x + k}{x - 1}$ =1的解为负数，则k的取值范围是．

查看试题解析
15. 如图，矩形ABCD中，对角线AC＝2 $\sqrt{3}$ ， E为BC边上一点，BC＝3BE，将矩形ABCD沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB＝．

查看试题解析
16. 如图，已知⊙C的半径为3，圆外一点O满足OC＝5，点P为⊙C上一动点，经过点O的直线l上有两点A、B，且OA＝OB，∠APB＝90°，l不经过点C，则AB的最小值为．

查看试题解析

三、解答题

17. 计算： $2 s i n 60 ° - (π - 3.14)^{0} + | 1 - \sqrt{3} | + (\frac{1}{2})^{- 1}$

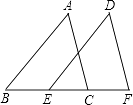
查看试题解析
18. 先化简，再求值： $\frac{x - 1}{x^{2} + 2 x + 1} \div (1 - \frac{2}{x + 1})$ ，其中 $x = \sqrt{3} - 1$ .

查看试题解析
19. 如图，已知点B、E、C、F在同一条直线上，AB=DE，∠A=∠D，AC∥DF．求证：BE=CF．

查看试题解析
20. 某校七年级（1）班班主任对本班学生进行了“我最喜欢的课外活动”的调查，并将调查结果分为书法和绘画类记为A；音乐类记为B；球类记为C；其他类记为D．根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动．班主任根据调查情况把学生都进行了归类，并制作了如下两幅统计图，请你结合图中所给信息解答下列问题：

(1)、七年级（1）班学生总人数为 ▲ 人，扇形统计图中D类所对应扇形的圆心角为 ▲ 度，请补全条形统计图；

(2)、学校将举行书法和绘画比赛，每班需派两名学生参加，A类4名学生中有两名学生擅长书法，另两名擅长绘画．班主任现从A类4名学生中随机抽取两名学生参加比赛，请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法，另一名擅长绘画的概率．

查看试题解析
21. 某校运动会需购买A，B两种奖品，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元.

(1)、求A、B两种奖品的单价各是多少元？

(2)、学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式.求出自变量m的取值范围，并确定最少费用W的值.

查看试题解析
22.
如图，CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角α=30°，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角β=60°，求树高AB（结果保留根号）

查看试题解析
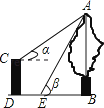23. 如图，直线y=﹣x+b与反比例函数y= $\frac{k}{x}$ 的图象相交于A（1，4），B两点，延长AO交反比例函数图象于点C，连接OB．

(1)、求k和b的值；

(2)、直接写出一次函数值小于反比例函数值的自变量x的取值范围；

(3)、在y轴上是否存在一点P，使S_△PAC= $\frac{2}{5}$ S_△AOB？若存在请求出点P坐标，若不存在请说明理由．

查看试题解析
24. 如图，PB为⊙O的切线，B为切点，直线PO交⊙O于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．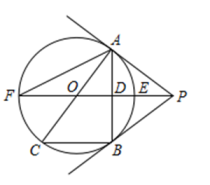

(1)、求证：直线PA为⊙O的切线；

(2)、求证： $A D \cdot A C = A P \cdot B C$

(3)、若BC=6， $t a n ∠ F = \frac{3}{4}$ 求⊙O的直径AC的长．

查看试题解析
25. 如图，抛物线y=ax²+bx+ 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C ，顶点为D ． E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G ．

(1)、求抛物线的函数解析式，并写出顶点D的坐标；

(2)、在直线EF上求一点H ，使△CDH的周长最小，并求出最小周长；

(3)、若点K在x轴上方的抛物线上运动，当K运动到什么位置时，
△EFK的面积最大？并求出最大面积．

查看试题解析