四川省泸州市泸县2022年中考数学一模试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

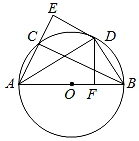
1. 方程x²﹣6x＝0的解是（）

A、x＝6 B、x＝0 C、x₁＝6，x₂＝0 D、x₁＝﹣6，x₂＝0

查看试题解析
2. 在平面直角坐标系中，点 $A (- 2 ， 1)$ 与点 $B$ 关于原点对称，则点 $B$ 的坐标为（）．

A、 $(- 2 ， 1)$ B、 $(2 ， - 1)$ C、 $(2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
3. 小明是校篮球队的一名队员，根据以往的数据统计，小明的进球率是50%，他明天将参加一场比赛，则下列说法正确的是（）

A、小明明天的进球率是50% B、小明明天每投10次必有5次投中 C、小明明天一定能进球 D、小明明天投20个球，其中投中10个是随机事件

查看试题解析
4. 如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）

A、 $\frac{C E}{C F} = \frac{E A}{F B}$ B、 $\frac{D E}{B C} = \frac{A D}{B D}$ C、 $\frac{A D}{A B} = \frac{A E}{A C}$ D、 $\frac{B D}{A B} = \frac{C F}{C B}$

查看试题解析
5. 已知△ABC∽△A'B'C'，AD和A'D'是它们的对应中线，若AD＝5，A'D'＝3，则△ABC与△A'B'C'面积的比是（）

A、3：5 B、9：25 C、5：3 D、25：9

查看试题解析
6. 如图，△ABC绕点C旋转，点B转到点E的位置，则下列说法正确的是（）

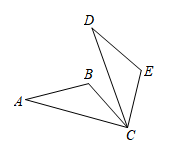A、点B与点D是对应点 B、∠BCD等于旋转角 C、点A与点E是对应点 D、△ABC≌△DEC

查看试题解析
7. 如图，在⊙O中，∠BDC＝25°，则∠BOC＝（）

A、30° B、40° C、50° D、60°

查看试题解析
8. 如图， $A B$ 是 $⊙ O$ 的弦，半径 $O C ⊥ A B$ 于点 $D ，$ 且 $A B = 6 cm ，$ $O D = 4 cm .$ 则 $D C$ 的长为（）.

A、 $5 cm$ B、 $2.5 cm$ C、 $2 cm$ D、 $1 cm$

查看试题解析
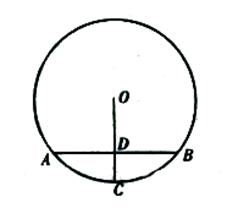9. 已知抛物线y=ax²+bx+c的图象如图所示，则关于x的方程ax²+bx+c=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有两个同号的实数根 D、没有实数根

查看试题解析
10. 已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（）

A、相交 B、相切 C、相离 D、不能确定

查看试题解析
11. 电影《长津湖》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，全国第一天票房约3亿元，假设以后每天票房按相同的增长率增长，第三天的票房收入约4亿元，若把增长率设为x，则下列方程正确的是（）

A、（1+x）²=4 B、3（1+x）²=4 C、3（1+x）³=4 D、（1+x）³=4

查看试题解析
12. 把二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象作关于x轴的对称变换，所得图象的解析式为 $y = - a (x - 1)^{2} + 4 a$ ，若 $(m - 1) a + b + c \leq 0$ ，则m的最大值为（）

A、-4 B、0 C、2 D、6

查看试题解析

二、填空题

13. 如图，圆内接四边形ABCD中，∠C＝120°，则∠A＝．

查看试题解析
14. 从编号为1到10的10张卡片中任取1张，所得编号是4的倍数的概率为．

查看试题解析
15. 若x＝3是关于x的方程2x²﹣9a＝0的一个根，则a的值为．

查看试题解析

三、解答题

16. 请阅读下列材料：
解方程：（x²﹣1）²﹣5（x²﹣1）+4＝0．

解法如下：

将x²﹣1视为一个整体，然后设x²﹣1＝y，则（x²﹣1）²＝y² ，

原方程可化为y²﹣5y+4＝0，

解得y₁＝1，y₂＝4．
（1）当y＝1时，x²﹣1＝1，解得x＝± $\sqrt{2}$ ；
（2）当y＝4时，x²﹣1＝4，解得x＝± $\sqrt{5}$ ．

综合（1）（2），可得原方程的解为x₁＝ $\sqrt{2}$ ， x₂＝﹣ $\sqrt{2}$ ， x₃＝ $\sqrt{5}$ ， x₄＝﹣ $\sqrt{5}$ ．

参照以上解法，方程x⁴﹣x²﹣6＝0的解为 .

查看试题解析
17. 解方程： ${(2 x - 1)}^{2} = {(3 - x)}^{2}$ ．

查看试题解析
18. 如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过O作OH⊥AC于点H．若OH＝3，AB＝12，BO＝13，求：⊙O的半径和AC的长．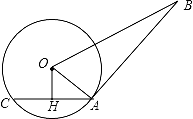

查看试题解析
19. 已知关于x的方程 $x^{2} - 4 x + k + 1 = 0$ 有两实数根.

(1)、求k的取值范围；

(2)、设方程两实数根分别为 $x_{1}$ 、 $x_{2}$ ，且 $\frac{3}{x_{1}} + \frac{3}{x_{2}} = x_{1} x_{2} - 4$ ，求实数k的值.

查看试题解析
20. 如图，正方形网挌中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点A（5，1），B（5，4），C（1，1）均在格点上．

(1)、将△ABC绕点C逆时针旋转90°后得到△A₁B₁C，画出△A₁B₁C；

(2)、求线段CB在旋转过程中扫过的面积（结果保留π）．

查看试题解析
21. 已知二次函数y＝x²﹣2x﹣3．

(1)、用配方法将y＝x²﹣2x﹣3化成y＝a（x﹣h）²+k的形式．并写出对称轴和顶点坐标；

(2)、在平面直角坐标系中，画出这个二次函数的简图；

(3)、当y随x的增大而减小时，求x的范围．

查看试题解析
22. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现：若每箱以50元的价格出售，平均每天可以销售80箱，价格每提高1元，平均每天少销售2箱．

(1)、求平均每天销售量y（箱）与销售价x（元/箱）（ $x \geq 50$ ）之间的函数关系式；

(2)、求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式；

(3)、当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？

查看试题解析
23. 为了解“停课不停学”期间，学生对线上学习方式的喜好情况，某校随机抽取40名学生进行问卷调查，其统计结果如表：
最喜欢的线上学习方式（每人最多选一种）
人数
直播
10
录播
a
资源包
5
线上答疑
8

(1)、求出a的值；

(2)、根据调查结果估计该校1000名学生中，最喜欢“线上答疑”的学生人数；

(3)、在最喜欢“资源包”的学生中，有2名男生，3名女生，现从这5名学生中随机抽取2名学生介绍学习经验，求恰好抽到1名男生和1名女生的概率．

查看试题解析
24. 如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交 $\overset{⌢}{B C}$ 于点D，过点D作DE∥BC交AC的延长线于点E.

(1)、求证：DE是⊙O的切线；

(2)、过点D作DF⊥AB于点F，连接BD.若OF＝1，BF＝2，求BD的长度.

查看试题解析
25. 如图，抛物线 $y = a x^{2} - 6 x + c$ 交x轴于 $A ， B$ 两点，交y轴于点C ．直线 $y = - x + 5$ 经过点 $B ， C$ ．

(1)、求抛物线的解析式；

(2)、抛物线的对称轴l与直线 $B C$ 相交于点P ，连接 $A C ， A P$ ，判定 $△ A P C$ 的形状，并说明理由；

(3)、在直线 $B C$ 上是否存在点M ，使 $A M$ 与直线 $B C$ 的夹角等于 $∠ A C B$ 的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析

最喜欢的线上学习方式（每人最多选一种）	人数
直播	10
录播	a
资源包	5
线上答疑	8