四川省攀枝花市2022年中考数学模拟试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 在﹣π，0，﹣2，2这四个数中，是负整数的是（）

A、﹣π B、﹣2 C、0 D、2

查看试题解析
2. 若 $2^{2 m + 1} + 4^{m} = 48$ ，则 $m$ 的值是（）

A、4 B、3 C、2 D、8

查看试题解析
3. 实数 $a ， b$ 在数轴上对应点的位置如图所示，则下列结论正确的是（）

A、 $a < b$ B、 $| a | < | b |$ C、 $a + b > 0$ D、 $a - b > 0$

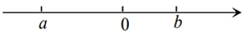查看试题解析
4. 如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图，则这个几何体的体积是（）

A、5 B、6 C、8 D、12

查看试题解析
5. 寻乌是中国脐橙之乡，去年销售脐橙27万吨，将数27万用科学记数法表示为（）．

A、2.7×10⁶ B、2.7×10⁵ C、0.27×10⁶ D、27×10⁴

查看试题解析
6. 已知 $f(1)=2$ (取 $1 \times 2$ 的末位数字)， $f(2)=6$ (取 $2×3$ 的末位数字)， $f(3)=2$ (取 $3 \times 4$ 的末位数字) …，则 $f (1) + f (2) + f (3) + \dots + f (2021)$ 的值为（）

A、6 B、4028 C、4042 D、4048

查看试题解析
7. 一位射击运动员在一次训练效果测试中射击了10次，成绩如图所示，对于这10次射击的成绩有如下结论，其中不正确的是（）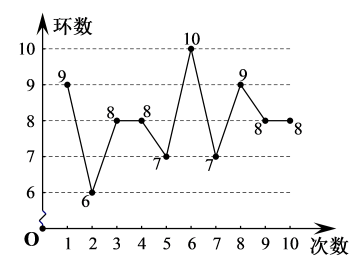

A、众数是8 B、中位数是8 C、平均数是8 D、方差是1

查看试题解析
8. 小刚把一块三角形玻璃打碎成了如图所示的三块，现要到玻璃店取配一块完全一样的玻璃，那么最省事的办法是（）

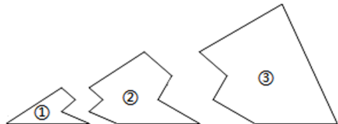A、带①去 B、带②去 C、带③去 D、带①和②去

查看试题解析
9. 在平面直角坐标系中，点 $A$ 的坐标是 $(- 1 ， 3)$ ，将原点 $O$ 绕点 $A$ 顺时针旋转 $90 °$ 得到点 $O^{'}$ ，则点 $O^{'}$ 的坐标是（）

A、 $(3 ， 1)$ B、 $(- 3 ， - 1)$ C、 $(- 4 ， 2)$ D、 $(2 ， 4)$

查看试题解析
10. 小明网购了一本《好玩的数学》，同学们想知道书的价格，小明让他们猜．甲说：“至少12元．”乙说“至多10元．”丙说“至多8元．”小明说：“你们三个人都说错了．”则这本书的价格x（元）所在的范围为（）

A、8＜x＜10 B、9＜x＜11 C、8＜x＜12 D、10＜x＜12

查看试题解析
11. 如图，OA是⊙O的半径，B为OA上一点(且不与点O、A重合)，过点B作OA的垂线交⊙O于点C ．以OB、BC为边作矩形OBCD ，连结BD ．若BD=10，BC=8，则AB的长为（）

A、8 B、6 C、4 D、2

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c$ 的部分图象如图所示，则下列结论中正确的是（）．

A、 $a > 0$ B、不等式 $a x^{2} + b x + c > 0$ 的解集是 $- 1 < x < 5$ C、 $a - b + c > 0$ D、当 $x > 2$ 时，y随x的增大而增大

查看试题解析

二、填空题

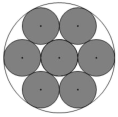
13. 设α，β是关于4x²﹣4mx+m+2＝0的两个实数根，当α²+β²有最小值时，则m的值为．

查看试题解析
14. 若（3﹣2x）：2＝（3+2x）：5，则x＝．

查看试题解析
15. 如图，一张圆形纸片中，画出7个同样大小的圆并涂上颜色．若一只蚂蚁（蚂蚁视为一点）随机的停留在该纸片上，则蚂蚁停留在涂有颜色部分的概率为．

查看试题解析
16. 如图，已知正方形 $A B C D$ 的边长为5，E为 $C D$ 边上一点（点E不与端点C，D重合，将 $△ A D E$ 沿 $A E$ 对折至 $△ A F E$ ，延长 $E F$ 交边 $B C$ 于点G，连接 $A G$ ， $C F$ ．以下结论：① $D E + B G = E G$ ；②若 $C F = F G$ ，则 $△ G E C$ 是等腰直角三角形；③若 $A G / / C F$ ，则 $D E = \frac{5}{2}$ ；④ $B G \cdot D E + A F \cdot G E = 25$ ．正确的有．（填序号）

查看试题解析

三、解答题

17. 解下列方程：

(1)、 $\frac{1}{x} = \frac{5}{x + 3}$ ；

(2)、 $\frac{x}{x - 1} = \frac{3}{2 x - 2} - 2$ ；

(3)、 $\frac{2}{2 x - 1} = \frac{1}{4 x^{2} - 1}$ ；

(4)、 $\frac{3}{x^{2} + 2 x} - \frac{1}{x^{2} - 2 x} = 0$ ；

(5)、 $\frac{x}{x - 3} = \frac{x + 1}{x - 1}$ ；

(6)、 $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ；

(7)、 $\frac{2 x + 1}{x^{2} + x} = \frac{5}{6 x + 6}$ ；

(8)、 $\frac{3}{2} - \frac{1}{3 x - 1} = \frac{5}{6 x - 2}$ ．

查看试题解析
18. 我市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一的外型、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如图所示的两幅不完整的统计图.

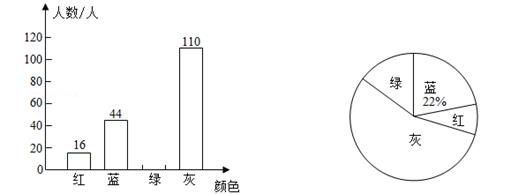
根据图中信息，解答下列问题：

(1)、此次调查一共随机采访了名学生，在扇形统计图中，“灰”所在扇形的圆心角的度数为度；

(2)、补全条形统计图（要求在条形图上方注明人数）；

(3)、若该校有3600名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；

(4)、李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图法或列表法求出恰好抽中A，B两人的概率.

查看试题解析
19. 如图，将直角三角形分割成一个正方形和两对全等的直角三角形，直角三角形ABC中，∠ACB＝90°，BC＝a，AC＝b，AB＝c，正方形IECF中，IE＝EC＝CF＝FI＝x

小明发明了求正方形边长的方法：

由题意可得BD＝BE＝a﹣x，AD＝AF＝b﹣x

因为AB＝BD+AD，所以a﹣x+b﹣x＝c，解得x＝ $\frac{a + b - c}{2}$

(1)、小亮也发现了另一种求正方形边长的方法：
利用S△ABC＝S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系，请根据小亮的思路完成他的求解过程：

(2)、请结合小明和小亮得到的结论验证勾股定理．

查看试题解析
20. 如图， $A C$ 是我市某大楼的高，在地面上 $B$ 点处测得楼顶 $A$ 的仰角为 $4 5^{∘}$ ，沿 $B C$ 方向前进 $18$ 米到达 $D$ 点，测得 $t a n ∠ A D C = \frac{5}{3}$ ．现打算从大楼顶端 $A$ 点悬挂一幅庆祝建国 $60$ 周年的大型标语，若标语底端距地面 $15 m$ ，请你计算标语 $A E$ 的长度应为多少？

查看试题解析
21. 如图，直线y＝ax﹣a与双曲线y＝ $\frac{k}{x}$ （k＞0）交于A、B两点，与x轴交于点D，与y轴交于点E，AC⊥y轴，垂足为点C．已知S_△_ACD＝2，B(﹣1，m)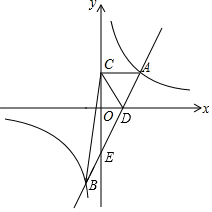

(1)、直接写出a与k的值．

(2)、求△ABC的面积．

查看试题解析
22. 如图，在梯形ABCD中，AD∥BC，AB＝DC＝8，∠B＝60°，BC＝12，连接AC．

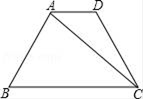(1)、求tan∠ACB的值；

(2)、若M、N分别是AB、DC的中点，连接MN，求线段MN的长．

查看试题解析
23. 如图，平行四边形ABCD的对角线AC，BD相交于点O，AB⊥AC，AB＝6cm，BC＝10cm，点P从点A出发，沿AD方向以每秒1cm的速度向终点D运动，连接PO，并延长交BC于点Q．设点P的运动时间为t秒．

(1)、求BQ的长（用含t的代数式表示）；

(2)、当四边形ABQP是平行四边形时，求t的值；

(3)、当 $t = \frac{32}{5}$ 时，点O是否在线段AP的垂直平分线上？请说明理由．

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x - 3$ 与x轴交于 $A (- 2 ， 0)$ 、 $B (6 ， 0)$ 两点，与y轴交于C点，设抛物线的顶点为D.过点D作 $D E ⊥ x$ 轴，垂足为E.P为线段DE上一动点， $F (m ， 0)$ 为x轴上一点，且 $P C ⊥ P F$ .

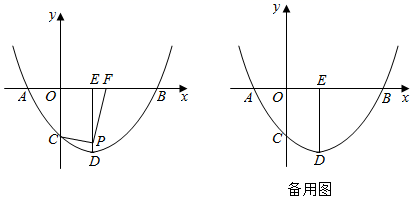(1)、求抛物线的解析式：

(2)、①当点P与点D重合时，求m的值；
②在①的条件下，将 $△ C O F$ 绕原点按逆时针方向旋转 $90 °$ 并平移，得到 $△ C_{1} O_{1} F_{1}$ ，点C，O，F的对应点分别是点 $C_{1}$ ， $O_{1}$ ， $F_{1}$ ，若 $△ C O F$ 的两个顶点恰好落在抛物线上，直接写出点 $F_{1}$ 的坐标；

(3)、当点P在线段DE上运动时，求m的变化范围.

查看试题解析