浙江省宁波市江北区部分校2021-2022学年九年级下学期期始测试数学试题（一模）

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 若 $3 x = 4 y,$ 则 $\frac{x}{y} =$ （）

A、 $\frac{3}{4}$ B、 $\frac{7}{4}$ C、 $\frac{4}{3}$ D、 $\frac{7}{3}$

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、经过红绿灯路口，遇到绿灯 B、射击运动员射击一次，命中靶心 C、班里有两名生日是同一天的同学 D、从一个只装有白球的袋中摸球，摸出白球

查看试题解析
3. 将如图所示的长方体牛奶包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形可能是（）

A、 B、 C、 D、

查看试题解析
4. 如图，已知 $A B / / C D / / E F$ ， $B D ： D F = 1 ： 2$ ，那么下列结论中，正确的是（）

A、 $A C ： A E = 1 ： 3$ B、 $C E ： E A = 1 ： 3$ C、 $C D ： E F = 1 ： 2$ D、 $A B ： E F = 1 ： 2$

查看试题解析
5. $R t △ A B C$ 中，斜边 $A B = 18$ ，其重心与外心之间的距离为（）

A、9 B、6 C、3 D、0

查看试题解析
6. sin70°，cos70°，tan70°的大小关系是（　　）

A、tan70°＜cos70°＜sin70° B、cos70°＜tan70°＜sin70° C、sin70°＜cos70°＜tan70° D、cos70°＜sin70°＜tan70°

查看试题解析
7. 如图，圆O与 $△ O A B$ 的边 $A B$ 相切，切点为 $B$ ．将 $△ O A B$ 绕点 $B$ 按顺时针方向旋转得到 $△ O^{'} A^{'} B$ ，使点 $O^{'}$ 落在圆O上，边 $A^{'} B$ 交线段 $A O$ 于点 $C$ ．若 $∠ A^{'} = 15 °$ ，半径长为2，则 $C B$ 的长度为（）．

A、 $\sqrt{3}$ B、2 C、 $\frac{3}{2}$ D、 $\frac{3}{2} \sqrt{3}$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，以 $R t △ A B C$ 各边为斜边分别向外作等腰 $R t △ A D B$ 、等腰 $R t △ A F C$ 、等腰 $R t △ B E C$ ，将等腰 $R t △ A D B$ 和等腰 $R t △ A F C$ 按如图方式叠放到等腰 $R t △ B E C$ 中，已知 $S_{四边形 G K J E} = 3$ ， $S_{四边形 K H C J} = 13$ ，则 $A C$ 长为（）

A、2 B、4 C、6 D、8

查看试题解析
9. 已知在平面直角坐标系xOy中，点A的坐标为(3，4)，M是抛物线 $y = a x^{2} + b x + 2$ (a≠0)对称轴上的一个动点，小明经探究发现：当 $\frac{b}{a}$ 的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定．当 $\frac{b}{a}$ 满足（）时，抛物线 $y = a x^{2} + b x + 2$ (a≠0)的对称轴上存在4个不同的点M，使△AOM为直角三角形.

A、 $0 < \frac{b}{a} < 2$ B、 $- 8 < \frac{b}{a} < 2$ C、 $- 3 \leq \frac{b}{a} < 0$ D、 $- 6 \leq \frac{b}{a} < 0$

查看试题解析
10. 已知 $△ A B C$ 与 $△ A B D$ 在同一平面内，点 $C$ ， $D$ 不关于AB对称， $∠ A B C = ∠ A B D = 30 °$ ， $A B = 2$ ， $A C = A D = \sqrt{2}$ ，则 $C D$ 长为（）

A、2或 $\sqrt{3} - 1$ B、2或 $\sqrt{6}$ C、 $\sqrt{3} - 1$ 或 $\sqrt{3} + 1$ D、2或 $\sqrt{3} + 1$

查看试题解析

二、填空题

11. 正六边形每个内角的度数为度.

查看试题解析
12. 一个不透明布袋中有2个红球，1个白球，这些球除颜色外无其他差别，从中随机模出一个小球，该小球是红色的概率为．

查看试题解析
13. 底面半径为1，母线长为2的圆锥的全面积等于．

查看试题解析
14. 如图，已知在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 2 \sqrt{3}$ ，点 $P$ 是 $A D$ 边上的一个动点，连接 $B P$ ，点 $C$ 关于直线 $B P$ 的对称点为 $C_{1}$ ，当点 $P$ 运动时，点 $C_{1}$ 也随之运动．若点 $P$ 从点A运动到点 $D$ ，则线段 $C C_{1}$ 扫过的区域的面积是．

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中， $∠ D A B$ ， $∠ A B C$ 的平分线 $A E$ ， $B F$ 分别与直线 $C D$ 交于点 $E$ ， $F$ ，当点 $D$ ， $F$ ， $E$ ， $C$ 相邻两点间的距离相等时，则 $\frac{A D}{A B}$ 的值为．

查看试题解析
16. 图1是邻边长为1和3的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图 $2)$ ，记图1中小正方形的中心为点 $A$ ， $B$ ， $C$ ，图2中的对应点为点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ．以大正方形的中心 $O$ 为圆心作圆，则当点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 三点中恰好有2点落在圆内时，圆面积S的取值范围为．

查看试题解析

三、解答题

17. 计算： $| - \sqrt{2} | + 2020^{0} - 2 \sqrt{2} \sin 30 ° + \sqrt[3]{8}$

查看试题解析
18. 如图，在 $6 \times 6$ 的网格中， $△ A B C$ 的三个顶点都在格点上.

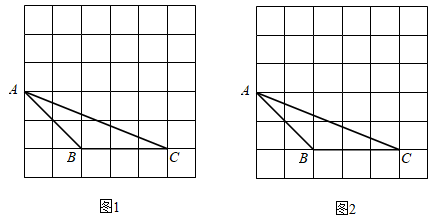(1)、在图1中画出 $△ A C D$ ，使 $△ A C D$ 与 $△ A C B$ 全等，顶点D在格点上.

(2)、在图2中过点B画出平分 $△ A B C$ 面积的直线l.

查看试题解析
19. 为落实疫情期间的垃圾分类，树立全面环保意识，某校举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为 $A$ ， $B$ ， $C$ ， $D$ 四个等级，并绘制了不完整的两种统计图：

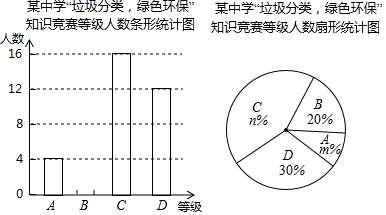
根据图中提供的信息，回答下列问题：

(1)、参加知识竞赛的学生共有 ▲ 人，并把条形统计图补充完整；

(2)、扇形统计图中， $m =$ ， $n =$ ， $C$ 等级对应的圆心角为度；

(3)、小明是四名获 $A$ 等级的学生中的一位，学校将从获 $A$ 等级的学生中任选取2人，参加市举办的知识竞赛，请用列表法或画树状图，求小明被选中参加区知识竞赛的概率.

查看试题解析
20. 拓展小组研制的智能操作机器人，如图1，水平操作台为l，底座AB固定，高AB为50cm，连杆BC长度为70cm，手臂CD长度为60cm.点B，C是转动点，且AB，BC与CD始终在同一平面内，

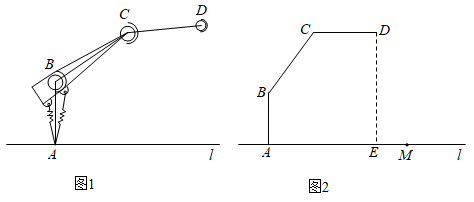(1)、转动连杆BC，手臂CD，使 $∠ A B C = 143 °$ ， $C D / / l$ ，如图2，求手臂端点D离操作台 $l$ 的高度DE的长（精确到1cm，参考数据： $\sin 53 ° \approx 0.8$ ， $\cos 53 ° \approx 0.6$ ）.

(2)、物品在操作台 $l$ 上，距离底座A端110cm的点M处，转动连杆BC，手臂CD，手臂端点D能否碰到点M？请说明理由.

查看试题解析
21. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于 $A (1 ， 0) ， B (3 ， 0 ）$ 两点，与y轴交于点 $C (0 ， - \frac{3}{2}) ， D$ 为顶点，连结 $B D ， C D$ 交x轴于点E.

(1)、求抛物线表达式；

(2)、求 $∠ O C D$ 的度数；

(3)、在y轴上是否存在一点P，使得 $△ C D P$ 与 $△ B D E$ 相似？若存在，求出P的坐标；若不存在，请说明理由.

查看试题解析
22. 等边△ABC与正方形DEFG如图1放置，其中D，E两点分别在AB，BC上，且BD＝BE．

(1)、求∠DEB的度数；

(2)、当正方形DEFG沿着射线BC方向以每秒1个单位长度的速度平移时，CF的长度y随着运动时间变化的函数图象如图2所示，且当t= $\sqrt{3}$ 时，y有最小值1；
①求等边△ABC的边长；
②连结CD，在平移的过程中，求当△CEF与△CDE同时为等腰三角形时t的值；
③从平移运动开始，到GF恰落在AC边上时，请直接写出△CEF外接圆圆心的运动路径的长度．

查看试题解析