浙江省绍兴市柯桥区2021-2022学年九年级下学期3月月考数学试题(一模)
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
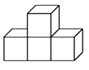
1. -2的绝对值是( )A、±2 B、2 C、 D、2. 如图是由四个相同的小正方体搭成的立体图形,它的主视图是( )
 A、
A、 B、
B、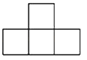 C、
C、 D、
D、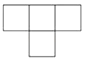 3. 一块某市政府特别奖奖牌如图所示,点A、B、D在圆O上,CD垂直平分AB于点C.现测得AB=CD=16cm,则圆形奖牌的半径为( )
3. 一块某市政府特别奖奖牌如图所示,点A、B、D在圆O上,CD垂直平分AB于点C.现测得AB=CD=16cm,则圆形奖牌的半径为( )
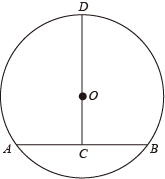 A、12cm B、10cm C、8cm D、6cm4. 关于x的一元二次方程的根的情况是( )A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中 、 分别表示一楼、二楼地面的水平线, , 的长是 ,则乘电梯从点 到点 上升的高度 是( )
A、12cm B、10cm C、8cm D、6cm4. 关于x的一元二次方程的根的情况是( )A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中 、 分别表示一楼、二楼地面的水平线, , 的长是 ,则乘电梯从点 到点 上升的高度 是( )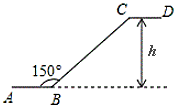 A、 B、 C、 D、6. 若(x﹣2)2=x2+mx+n,则m,n的值分别是( )A、4,4 B、﹣4,4 C、﹣4,﹣4 D、4,﹣47. 篮球队5名场上队员的身高(单位:cm)分别是:188,190,192,194,195.现用一名身高为191cm的队员换下身高为195cm的队员,与换人前相比,场上队员的身高( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大8. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=3,BD是△ABC的中线,过点C作CP⊥BD于点P,图中阴影部分的面积为( )
A、 B、 C、 D、6. 若(x﹣2)2=x2+mx+n,则m,n的值分别是( )A、4,4 B、﹣4,4 C、﹣4,﹣4 D、4,﹣47. 篮球队5名场上队员的身高(单位:cm)分别是:188,190,192,194,195.现用一名身高为191cm的队员换下身高为195cm的队员,与换人前相比,场上队员的身高( )A、平均数变小,方差变小 B、平均数变小,方差变大 C、平均数变大,方差变小 D、平均数变大,方差变大8. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=3,BD是△ABC的中线,过点C作CP⊥BD于点P,图中阴影部分的面积为( )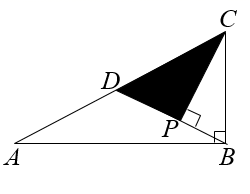 A、 B、 C、 D、9. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.下列说法错误的是( )
A、 B、 C、 D、9. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.下列说法错误的是( )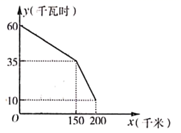 A、该汽车的蓄电池充满电时,电量是60千瓦时 B、蓄电池剩余电量为35千瓦时,汽车已行驶了150千米 C、当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时 D、25千瓦时的电量,汽车能行驶10. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )
A、该汽车的蓄电池充满电时,电量是60千瓦时 B、蓄电池剩余电量为35千瓦时,汽车已行驶了150千米 C、当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时 D、25千瓦时的电量,汽车能行驶10. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )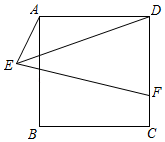 A、12 B、12 C、12 D、10
A、12 B、12 C、12 D、10二、填空题
-
11. 分解因式:a3﹣9a= .
12. 为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:视力
4.7以下
4.7
4.8
4.9
4.9以上
人数
102
98
80
93
127
根据抽样调查结果,估计该区12000名初中学生视力不低于4.8的人数是.
13. 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为cm.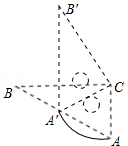 14. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .15. 过双曲线 的动点 作 轴于点 , 是直线 上的点,且满足 ,过点 作 轴的平行线交此双曲线于点 .如果 的面积为8,则 的值是 .16. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形可以制作一副如图1所示的七巧板,现将这副七巧板拼成如图2所示的造型恰好放入矩形ABCD中(其中点E,F,G,H,K都在矩形边上),则AD长是.
14. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .15. 过双曲线 的动点 作 轴于点 , 是直线 上的点,且满足 ,过点 作 轴的平行线交此双曲线于点 .如果 的面积为8,则 的值是 .16. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形可以制作一副如图1所示的七巧板,现将这副七巧板拼成如图2所示的造型恰好放入矩形ABCD中(其中点E,F,G,H,K都在矩形边上),则AD长是.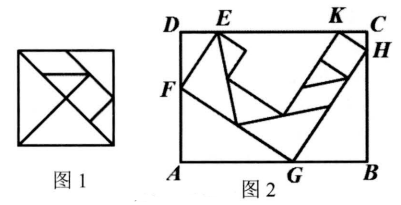
三、解答题
-
17.(1)、计算:;(2)、解不等式组: .18. 一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为 .(1)、布袋里红球有多少个?(2)、先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或树状图等方法求出两次摸到的球是1个红球和1个白球的概率.19. 以下各图均是由边长为1的小正方形组成的网格, 均在格点上.
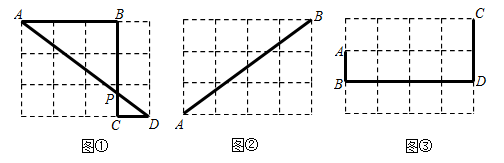 (1)、在图①中,的值为;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图①中,的值为;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图②,在上找一点 , 使;
②如图③,在上找一点 , 使 .
20. 如图①,将“欢迎光临”门挂便斜放置时,测得挂绳的一段 cm.另一段 cm.已知两个固定扣之间的距离 cm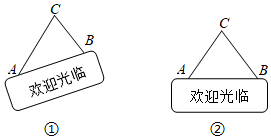 (1)、求点 到 的距离;(2)、如图②,将该门挂扶“正”(即 ),求 的度数.(参考数据: , , , , )21. 如图,四边形ABCD是平行四边形,DE⊥BC于点E,CF⊥AB交AB的延长线于点F.
(1)、求点 到 的距离;(2)、如图②,将该门挂扶“正”(即 ),求 的度数.(参考数据: , , , , )21. 如图,四边形ABCD是平行四边形,DE⊥BC于点E,CF⊥AB交AB的延长线于点F.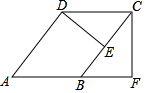 (1)、求证:△CBF∽△DCE;(2)、若点E恰为BC中点,且AB=6,BF=4,求AD的长.22. “双减”政策落地后,对校外培训机构的影响巨大,不管是机构还是机构老师都面临着转型,培训机构李老师推出了“热学文化”新零售项目.他新开了甲、乙两家分店共同销售,因地段不同,甲店一天可售出某品牌科技产品20件,每件盈利26元;乙店一天可售出同一品牌科技产品32件,每件盈利20元.经调查发现,每件此种科技产品每降价1元,甲、乙两家店一天都可多售出2 件.设甲店每件降价a元时,一天可盈利y1元,乙店每件降价b元时,一天可盈利y2元.(1)、当a=5时,求y1的值.(2)、求y2关于b的函数表达式.(3)、若李老师规定两家分店下降的价格必须相同,请求出每件此种科技产品下降多少元时,两家分店一天的盈利和最大,最大是多少元?23. 定义:有一组邻边相等且对角互补的四边形叫做等补四边形.(1)、阅读与理解:
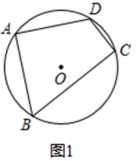
(1)、求证:△CBF∽△DCE;(2)、若点E恰为BC中点,且AB=6,BF=4,求AD的长.22. “双减”政策落地后,对校外培训机构的影响巨大,不管是机构还是机构老师都面临着转型,培训机构李老师推出了“热学文化”新零售项目.他新开了甲、乙两家分店共同销售,因地段不同,甲店一天可售出某品牌科技产品20件,每件盈利26元;乙店一天可售出同一品牌科技产品32件,每件盈利20元.经调查发现,每件此种科技产品每降价1元,甲、乙两家店一天都可多售出2 件.设甲店每件降价a元时,一天可盈利y1元,乙店每件降价b元时,一天可盈利y2元.(1)、当a=5时,求y1的值.(2)、求y2关于b的函数表达式.(3)、若李老师规定两家分店下降的价格必须相同,请求出每件此种科技产品下降多少元时,两家分店一天的盈利和最大,最大是多少元?23. 定义:有一组邻边相等且对角互补的四边形叫做等补四边形.(1)、阅读与理解:如图1,四边形内接于⊙O,点A为弧BD的中点.四边形ABCD(填“是”或“不是”)等补四边形.
 (2)、探究与运用:
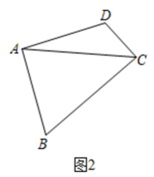
(2)、探究与运用:①如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由;
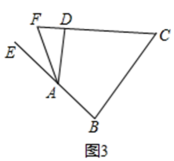
②如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,若CD=10,AF=5,求DF的长.
 (3)、思考与延伸:
(3)、思考与延伸:在等补四边形ABCD中,AB=AD=3,∠BAD=120°,当对角线AC长度最大时,以AC为斜边作等腰直角三角形ACP,直接写出线段DP的长度.
24. 在平面直角坐标系中,已知点A(0,3),点B在线段AO上,且AB=2BO,若点P在x轴的正半轴上,连接BP,过点P作PQ⊥PB.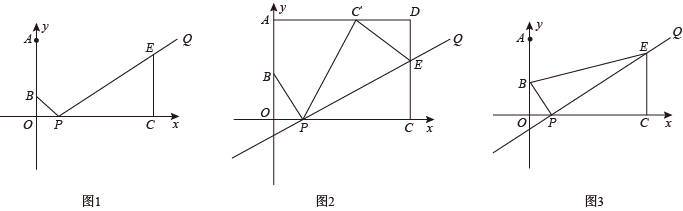 (1)、如图1,点E是射线PQ上一点,过点E作EC⊥x轴,垂足为点C,求证:△BOP∽△PCE;(2)、在(1)的条件下,如图2,若点C坐标为(4,0).过点A作DA⊥y轴,且和CE的延长线交于点D,若点C关于直线PQ的对称点C′正好落在线段AD上.连接PC′,求点P的坐标.(3)、如图3,若∠BPO=60°,点E在直线PQ上,EC⊥x轴,垂足为点C,若以点E,P,C为顶点的三角形和△BPE相似,请直接写出点E的坐标.
(1)、如图1,点E是射线PQ上一点,过点E作EC⊥x轴,垂足为点C,求证:△BOP∽△PCE;(2)、在(1)的条件下,如图2,若点C坐标为(4,0).过点A作DA⊥y轴,且和CE的延长线交于点D,若点C关于直线PQ的对称点C′正好落在线段AD上.连接PC′,求点P的坐标.(3)、如图3,若∠BPO=60°,点E在直线PQ上,EC⊥x轴,垂足为点C,若以点E,P,C为顶点的三角形和△BPE相似,请直接写出点E的坐标.