浙江省温州市文成县2021年中考适应性数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个实数2，0，1，－1，其中最小的是（）

A、2 B、1 C、0 D、－1

查看试题解析
2. 计算a³÷a²的结果是（）

A、a B、a⁵ C、a⁶ D、a⁹

查看试题解析
3. 如图是由5个完全相同的小正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析

4. 某同学将自己7次体育测试成绩（单位：分）统计如下表，则该同学7次体育测试成绩的众数是（）

次数	第一次	第二次	第三次	第四次	第五次	第六次	第七次
成绩	35	37	37	37	38	38	39

A、35分 B、37分 C、38分 D、39分

查看试题解析

5. 使式子 $\sqrt{\frac{1}{x + 1}}$ 有意义的x取值范围是（）

A、x＞－1 B、x≥－1 C、x＜－1 D、x≠－1

查看试题解析
6. 六边形的内角和为（）

A、360° B、540° C、720° D、900°

查看试题解析
7. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两(我国古代货币单位)；马三匹、牛五头，共价三十八两．问马、牛各价几何?”设马每匹 $x$ 两，牛每头 $y$ 两，根据题意可列方程组为（）

A、 ${\begin{cases} 4 x + 6 y = 38 \\ 3 x + 5 y = 48 \end{cases}$ B、 ${\begin{cases} 4 y + 6 x = 48 \\ 3 y + 5 x = 38 \end{cases}$ C、 ${\begin{cases} 4 x + 6 y = 48 \\ 5 x + 3 y = 38 \end{cases}$ D、 ${\begin{cases} 4 x + 6 y = 48 \\ 3 x + 5 y = 38 \end{cases}$

查看试题解析
8. 如图，图①是一种携带方便的折叠凳子，图②是它的侧面图示，已知凳腿AD＝BC＝4分米，当凳腿AD与水平地面CD的夹角为 $α$ 时人坐着最舒服，此时凳面AB离地面CD的高度为（）

A、 $4 s i n α$ 分米 B、 $4 c o s α$ 分米 C、 $\frac{4}{s i n α}$ 分米 D、 $\frac{4}{c o s α}$ 分米

查看试题解析
9. 如图，菱形ABCD在第一象限，且对角线 $A C ∥ x$ 轴，点C，D在反比例函数 $y = \frac{k}{x}$ 的图象上，已知A(3，4)，B(6，a)则k的值为（）

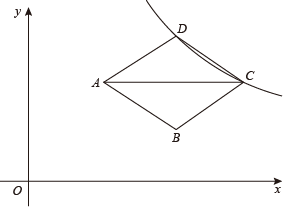A、24 B、32 C、36 D、48

查看试题解析
10. 如图，在 $R t △ A B C$ 中，∠ACB＝90°，分别以其三边向外作正方形，过点C作CK⊥AB交ID于点K，延长EB交AG于点L，若点L是AG的中点， $△ A B C$ 的面积为20，则CK的值为（）

A、4 B、5 C、 $2 \sqrt{5}$ D、 $4 \sqrt{5}$

查看试题解析

二、填空题

11. 因式分解： $m^{2} - 6 m =$ ．

查看试题解析
12. 某校竞选学生会主席，其中某位候选人自我介绍、竞选演讲和随机提问三轮评审团评分为92分、85分，90分，自我介绍占40%，竞选演讲占40%，随机提问占20%，则该候选人的综合成绩为分．

查看试题解析
13. 若扇形的弧长为 $\frac{3}{4} π$ ，圆心角为45°，则该扇形的半径为．

查看试题解析
14. 某班同学，每人都会打篮球或踢足球，其中会打篮球的人数比会踢足球的人数多12人，两种都会的有8人，设会踢足球的有a人，则该班同学共有人（用含a的代数式表示）．

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 6$ ， $B C = 8$ ， $∠ B A C$ ， $∠ A C B$ 的平分线相交于点E，过点E作 $E F / / B C$ 交AC于点F，则 $E F =$ ；

查看试题解析
16. 图形甲是小明设计的花边作品，该作品是由形如图形乙通过对称和平移得到．在图乙中，△AEO≌△ADO≌△BCO≌△BFO，E，O，F均在直线MN上，EF=12，AE=14，则OA长为，若连接OG，则OG的长为．

查看试题解析

三、解答题

17. 计算：

(1)、 $| - 5 | + \sqrt{25} - {(2020 - \sqrt{3})}^{0}$ ；

(2)、x（1－x）+（x+1）（x－1）．

查看试题解析
18. 如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，连接AE，CF．

(1)、求证： $△ A B E ≌ △ C D F$ ．

(2)、若∠BAC＝90°，AB＝3，AC＝8，求AE的长．

查看试题解析
19. “停课不停学”，某校为了了解学生在钉钉直播课中观看直播课时间（一节课30分钟），随机抽取了若干名学生观看直播课的时间，获得数据如表，并绘制了相应的扇形统计图．
被抽取学生观看直播课时间统计表：
观看直播课时间
人数
27＜t≤30
20
24＜t≤27
15
21＜t≤24
10
18＜t≤21
m
15＜t≤18
1
t≤15
1

(1)、请问被随机抽取的学生共有多少名？并求表格中m的值．

(2)、在扇形统计图中，求观看时间在24＜1≤27的学生人数所对的扇形圆心角的度数．

(3)、若该校共有学生1100名，估计观看直播课时间在21分钟以上（不包括21分钟）的有多少人？

查看试题解析
20. 图1，图2均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A，B，E，F均在格点上，在图①，图②中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

(1)、在图①中画一个等腰直角三角形ABC．

(2)、在图②中以线段EF为边画一个四边形EFGH，使其面积为9，且∠EFG＝90°．

查看试题解析
21. 已知抛物线y＝－x²+bx+c过点A（2，0），B（－4，0）．

(1)、求b，c的值．

(2)、设抛物线顶点处有一点C，将点C沿抛物线的对称轴向下平移m个单位，使AC＝5，求m的值．

查看试题解析
22. 如图，直线CF与⊙O交于点D，E，点A，B在⊙O上，且 $\overset{⌢}{A B} = \overset{⌢}{B D} = \overset{⌢}{A E}$ ， BC与⊙O切于点B．

(1)、求证：四边形ABCD是平行四边形．

(2)、若CF＝22，∠C＝45°， $s i n ∠ F ＝ \frac{5}{13}$ ，求⊙O的半径．

查看试题解析
23. 文成县一支参赛队准备请一个刺绣师为他们的队旗绣一个队微，队徽是以“文”字的拼音首字母“W”为主要造型．如图，长方形EFPQ的长EQ＝40cm，宽EF＝18cm，整个图形关于直线AG对称，且AB∥CD，AD∥BC，BM∥EC，CF＝12 cm，EM：BC＝2：3．为使图案美观，EM不能超过AM的 $\frac{1}{3}$ ．刺绣师准备在甲，乙，丙三个区域分别以不同的刺绣手法刺绣，其中甲区域是指“W”范围，乙区域是指“W”上方的两个三角形范围，丙是指整个长方形除去甲，乙的部分，设EM＝xcm．

(1)、当x为何值时，丙区域的面积恰好为306平方厘米．

(2)、求甲区域面积关于x的函数关系式，并求甲面积的最大值．

(3)、若甲，乙，丙三个区域每平方厘米刺绣的针数分别为5n，5n，4n（n为正整数），甲乙的总针数之和比丙的总针数多15840针，则甲区域每平方厘米至少需要绣针（直接写出答案）．

查看试题解析
24. 如图，在 $△ A B C$ 中，AB＝AC，H是BA上的点，且∠A＝2∠BCH．点M是AC的中点，当点Q从点M匀速运动到点C时，点P恰好从点H匀速运动到点A，记MQ＝x，BP＝y，已知y＝kx+b（k≠0）．

(1)、求证： $△ A C H$ 是直角三角形．

(2)、若 $k = \frac{8}{5}$ ， b＝2，
①求BH、AC的长．
②连接PQ，BM和HM．当PQ与 $△ B H M$ 的一边垂直时，请求出所有满足条件的x的值．

(3)、若 $k = \frac{4}{3}$ ，当 $P Q ∥ B C$ 时，PQ交HM于N，连接CN，AN，请直接写出 $△ C N Q$ 与 $△ A N P$ 面积的比值．

查看试题解析

观看直播课时间	人数
27＜t≤30	20
24＜t≤27	15
21＜t≤24	10
18＜t≤21	m
15＜t≤18	1
t≤15	1