浙江省温州市瓯海区2022年第一次模拟考试数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数最大的是（）

A、﹣1 B、﹣ $\frac{1}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
2. 自2015年北京冬奥会成功申办以来，截至2021年10月，全国居民参与过冰雪运动的人数约为346000000人，实现了“带动三亿人参与冰雪运动”的目标．其中346000000用科学记数法表示为（）

A、346×10⁶ B、3.46×10⁶ C、3.46×10⁸ D、3.46×10⁹

查看试题解析
3. 一个不透明袋子中有3个红球，4个白球，2个黑球，它们除颜色外其余都相同．从中任意摸出一个球是白球的可能性是（）

A、 $\frac{2}{9}$ B、 $\frac{3}{9}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
4. 三通管的立体图如图所示，则这个几何体的俯视图是（）．

A、 B、 C、 D、

查看试题解析
5. 有甲、乙两组数据，已知甲组数据的方差为0.5，乙组数据的方差为0.2，那么甲、乙两组数据的波动程度是（）

A、甲组数据的波动比较大 B、乙组数据的波动比较大 C、甲、乙两组数据的波动程度相同 D、甲、乙两组数据的波动程度无法比较

查看试题解析
6. 如图，PC，PB分别切⊙O于点C，B．若AB是直径，∠A＝55°，则∠P的度数为（）

A、55° B、70° C、80° D、85°

查看试题解析

7. 关于x的方程x（x﹣1）＝3（x﹣1），下列解法完全正确的是（）

两边同时除以（x﹣1）得，x＝3

整理得，x²﹣4x＝﹣3∵a＝1，b＝﹣4，c＝﹣3，

b²﹣4ac＝28

∴x＝ $\frac{4 \pm \sqrt{28}}{2}$ ＝2± $\sqrt{7}$

整理得，x²﹣4x＝﹣3配方得，x²﹣4x+2＝﹣1

∴（x﹣2）²＝﹣1

∴x﹣2＝±1

∴x₁＝1，x₂＝3

移项得，（x﹣3）（x﹣1）＝0∴x﹣3＝0或x﹣1＝0

∴x₁＝1，x₂＝3

A、A B、B C、C D、D

查看试题解析

8. 如图把两张宽度均为3的纸条交错叠在一起，相交成角α，则重叠部分的周长为（）

A、12tanα B、12sinα C、 $\frac{12}{s i n α}$ D、 $\frac{12}{t a n α}$

查看试题解析
9. 已知点A（﹣1，m），B（1，m），C（2，m﹣3）在同一个函数的图象上，这个函数可能是（）

A、y＝x B、y＝﹣ $\frac{2}{x}$ C、y＝x² D、y＝﹣x²

查看试题解析
10. 如图，在△ABC中，∠BAC＝90°，以BC为边向上作正方形BCDE，以AC为边作正方形ACFG，点D落在GF上，连结AE，EG．若DG＝2，BC＝6，则△AEG的面积为（）

A、4 B、6 C、5 $\sqrt{2}$ D、8

查看试题解析

二、填空题

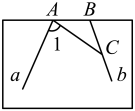
11. 因式分解a²﹣4a+4的结果是．

查看试题解析
12. 不等式组 ${\begin{matrix} 3 x - 2 > x \\ \frac{1}{2} x \leq 3 \end{matrix}$ 的解是.

查看试题解析
13. 已知扇形的弧长为2πcm，半径为3cm，则该扇形的面积为cm² ．

查看试题解析
14. 小芳和小林为了研究图中“跑到画板外面去的两直线a，b所成的角（锐角）”问题，设计出如下两个方案：
小林的方案
小芳的方案
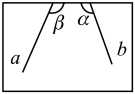
测α，β的度数．
测∠1，∠ACB的度数．
已知小林测得∠β＝115°，小芳作了AB＝BC，并测得∠1＝80°，则直线a，b所成的角为．

查看试题解析
15. 如图，菱形ABCD的对角线交于点E，边CD交y轴正半轴于点F，顶点A，D分别在x轴的正、负半轴上，反比例函数y＝ $\frac{k}{x}$ 的图象经过C，E两点，过点E作EG⊥OA于点G，若CF＝2DF，DG﹣AG＝3，则k的值是．

查看试题解析
16. 图1是一张矩形折纸，其中图形①，③，⑤分别与图形②，④，⑥关于AB所在的直线成轴对称，现沿着虚线剪开，部分剪纸拼成不重叠、无缝隙的正方形（如图2），若正方形边长为9，图2中所标注的d₁的值为6，d₂的值为整数，则图1中矩形的宽为，矩形的长为．

查看试题解析

三、解答题

17.

(1)、计算：（﹣2）²× $\frac{3}{2}$ +|﹣5|﹣ $\sqrt{9}$ ．

(2)、化简： $\frac{a^{2}}{a^{2} - 2 a} + \frac{4}{2 a - a^{2}}$ ．

查看试题解析
18. 如图，在△ABC与△DCB中，AC与BD交于点E，且∠A＝∠D，AE＝DE．

(1)、求证：△ABE≌△DCE．

(2)、当∠A＝90°，AB＝4，AE＝3时，求BC的值．

查看试题解析
19. 瓯海区在推进“防范网络诈骗”的行动中，某街道对甲，乙两个小区各随机选择100位居民进行问卷调查，并将调查结果分为A表示“非常了解”，B表示“比较了解”，C表示“基本了解”，D表示“不了解”四个等级进行统计分析，并绘制如下的统计图．

(1)、若甲小区共有常住居民1000人，请估计整个甲小区达到“非常了解”的居民人数．

(2)、若给A，B，C，D四个等级分别以5，3，1，0进行赋分，请结合你所学习的统计知识，选出你认为防范网络诈骗普及工作更出色的小区？通过计算并用合适数据多角度说明．

查看试题解析
20. 如图在8×8的方格纸ABCD中，M，N分别是AD，AB的中点，请按要求画格点线段（端点在格点上），且所画的线段端点均不与点A，B，C，D重合．

(1)、在图1中画一条格点线段EF平分MN，使E，F在四边形ABCD的边上，且不与它的边平行．

(2)、在图2中画一条格点线段GH，使得MN平分GH，且G，H在四边形ABCD的边上．

查看试题解析
21. 如图，抛物线y＝﹣x²+bx+c与x轴分别交于点A（﹣1，0），B（3，0）．

(1)、求抛物线的函数表达式和对称轴．

(2)、P为y轴上的一点．若点P向左平移n个单位，将与抛物线上的点P₁重合；若点P向右平移2n个单位，将与抛物线上的点P₂重合．已知n＞0．
①求n的值．
②若点C在抛物线上，且在直线P₁P₂的上方（不与点P₁ ， P₂重合），求点C纵坐标的取值范围．

查看试题解析
22. 如图，四边形ABCD内接于⊙O，AC是⊙O的直径，作DE∥BC，交BO的延长线于点E，且BE平分∠ABD．

(1)、求证：四边形BCDE是平行四边形；

(2)、若AD＝8，tan∠BDE＝ $\frac{3}{4}$ ，求AC的长与▱BCDE的周长．

查看试题解析
23. 某公司在甲、乙工厂代工同一产品，表1是两个工厂产品的收费标准，表2是两个工厂的代工记录（a，b为常数，m，n都为不大于10的正整数），代工费用由加工费和制版费两部分组成，制版费与件数无关．已知甲、乙两工厂第一次代工合计500件，且两工厂收费相同．
表1
收费内容工厂
单件加工费
制版费
甲
10元
2000元
乙
25元
0
表2
时间
甲工厂代工记录
乙工厂代工记录
第一次
a件
b件
第二次
（a+100m）件
（b+100n）件

(1)、求a，b的值．

(2)、若m+n＝12，第二次分配到甲工厂的代工件数小于分配到乙工厂的代工件数的2倍，求甲、乙两工厂第二次代工总费用的最小值．

(3)、若甲工厂代工效率为20件每小时，乙工厂代工效率为40件每小时，第二次甲、乙两工厂代工总费用估计在42000到44000元之间（包括42000，44000），求出所有满足条件的代工分配方案，并指出哪种方案代工总时长最短．

查看试题解析
24. 如图，在Rt△ABC中，∠ABC＝90°，D是BC上的一点，且∠BAD＝∠ACB，DE⊥AC于点F，交BC的平行线AE于点E．

(1)、求证：AD＝DE．

(2)、若BD＝ $\frac{\sqrt{15}}{3}$ ， CD＝ $\sqrt{15}$ ．
①求AC的长．
②过点E作EG⊥AD于点G，在射线AC上取一点M与△AEG某一边的两端点，构成以M为顶点的角等于∠ACB，求所有满足条件的AM的长．

查看试题解析

小林的方案	小芳的方案

测α，β的度数．	测∠1，∠ACB的度数．

收费内容工厂	单件加工费	制版费
甲	10元	2000元
乙	25元	0

时间	甲工厂代工记录	乙工厂代工记录
第一次	a件	b件
第二次	（a+100m）件	（b+100n）件