浙江省宁波市2022年初中学业水平考试原创数学模拟试卷（甬真卷B）

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、选择题（每小题4分，共40分。）

1. ﹣9的绝对值是（）

A、9 B、﹣9 C、 $\frac{1}{9}$ D、﹣ $\frac{1}{9}$

查看试题解析
2. 计算2a³•5a³的结果是（）

A、10a⁶ B、10a⁹ C、7a³ D、7a⁶

查看试题解析
3. 第七次全国人口普查结果显示，我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为（）

A、 $218 \times 10^{6}$ B、 $21.8 \times 10^{7}$ C、 $2.18 \times 10^{8}$ D、 $0.218 \times 10^{9}$

查看试题解析
4. 如图是由5个完全相同的小正方体组成的几何体，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
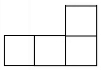5. 有7名学生的鞋号（单位：厘米）由小到大是：20，21，22，22，23，23，23，则这组数据的中位数和众数分别是（）

A、20，21 B、21，22 C、22，22 D、22，23

查看试题解析
6. 二次根式 $\sqrt{x - 3}$ 中字母x的取值范围是（）

A、x＞3 B、x≠3 C、x≥3 D、x≤3

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，点E，F分别在AB，AC上，AF=EF.若∠CFE=72°则∠B的度数为（）

A、56° B、54° C、46° D、44°

查看试题解析
8. 我国古代数学菩作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步，问：人与车各几何？”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少？设共有x人，y辆车，则可列方程组为（）

A、 ${\begin{cases} 3 (y - 2) = x \\ 2 y - 9 = x \end{cases}$ B、 ${\begin{cases} 3 (y + 2) = x \\ 2 y + 9 = x \end{cases}$ C、 ${\begin{cases} 3 (y - 2) = x \\ 2 y + 9 = x \end{cases}$ D、 ${\begin{cases} 3 (y - 2) = x \\ 2 y + x = 9 \end{cases}$

查看试题解析
9. 已知正比例函数y＝k₁x和反比例函数y＝ $\frac{k_{2}}{x}$ ，在同一直角坐标系下的图象如图所示，其中符合k₁•k₂＞0的是（）

A、①② B、①④ C、②③ D、③④

查看试题解析
10. 如图，正方形ABCD被分成五个面积相等的矩形，若FG=4，则正方形的面积为（）

A、64 B、 $\frac{225}{4}$ C、49 D、36

查看试题解析

二、填空题（每小题5分，共30分）

11. 6的相反数为．

查看试题解析
12. 分解因式：x²﹣2x＝．

查看试题解析
13. 不透明袋子中装有1个红球，5个黑球，4个白球，这些球除颜色外无其他差别，从袋子中随机摸出一个球，则摸出红球的概率是．

查看试题解析
14. 如图是圆弧形状的铁轨示意图，半径OA的长度为200米，圆心角∠AOB=90°，则这段铁轨的长度为米．（铁轨的宽度忽略不计，结果保留π）

查看试题解析
15. 如图，已知⊙O半径为3，点A为圆外一点，点B在圆上，当△AOB为直角三角形时，△AOB面积为6，则OA的长为．

查看试题解析
16. 如图①，在菱形ABCD中，点E为BC的中点，点F为AD上一动点.将四边形FECD沿着EF翻折，得到四边形FEC'D'，C'E与AB交于点P

(1)、如图①，若点F与点A重合时，恰有FP＝FE，则 $\frac{A P}{B P}$ = ．

(2)、在（1）问的结论下，如图② ，当AF平分∠EFD'时， $\frac{E F}{C D}$ 的值为．

查看试题解析

三、解答题（本大题有8小题，共80分）

17.

(1)、计算：x（x+2）+（1+x）（1﹣x）；

(2)、解不等式组： ${\begin{cases} 2 x + 3 < 9 \\ 2 - x \leq 0 \end{cases}$ ．

查看试题解析
18. 如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上，

(1)、在图①中画出以AB为边且周长为6 $\sqrt{5}$ 的平行四边形ABCD，且点C和点D均在格点上

(2)、在图②中画出以AB为对角线的正方形AEBF，且点E和点F均在格点上，

查看试题解析
19. 如图，二次函数y＝（x+1）（x+a）（a为常数）的图象的对称轴为直线x=1.

(1)、求a的值.

(2)、向上平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式。

查看试题解析
20. 高尔基说：“书，是人类进步的阶梯，”阅读可以启智增慧，拓展视野.，为了解学生寒假阅读情况，开学初学校进行了问卷调查，并对部分学生假期（24天）的阅读总时间做了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为（小时），阅读总时间分为四个类别：A（0<t<12），B（12≤t<24），C（24≤t<36），D（t≥36），将分类结果制成如下两幅统计图（尚不完整）.

根据以上信息，回答下列问题：

(1)、本次抽样的样本容量为

(2)、补全条形统计图：

(3)、扇形统计图中a的值为，圆心角β的度数为

(4)、若该校有2000名学生，估计寒假阅读的总时间少于24小时的学生有多少名？对这些学生用一句话提一条阅读方面的建议.

查看试题解析
21. 据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过50km/h.如图，在一条笔直公路l的上方A处有一深测仪，AD⊥l于D，AD=32m，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=28°，2秒后到达C点，测得∠ACD=45°（sin28°≈ $\frac{8}{17}$ ， cos28°≈ $\frac{15}{17}$ ， tan28°≈ $\frac{8}{15}$ ）

(1)、求CD，BD的长度.

(2)、通过计算，判断此轿车是否超速.

查看试题解析
22. 小甬星期天从家里出发骑车去舅舅家做客，当他骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，如图是他本次去舅舅家所用的时间与小甬离家的距离的关系示意图.根据图中提供的信息回答下列问题：

(1)、小甬家到舅舅家的路程是米，小甬在商店停留了分钟；

(2)、在整个去舅舅家的途中哪个时间段小甬骑车速度最快？最快的速度是多少米/分？

(3)、本次去舅舅家的行程中，小甬一共行驶了多少米？

查看试题解析
23. 如图

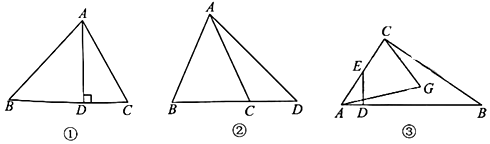(1)、【基础巩固】如图①，在△ABC中，AD⊥BC于点D，若BD=3，CD=1，求AB²-AC²的值；

(2)、【尝试应用】如图②，点C在△ABD的边BD上，满足AB=AC，求证：AD²-AC²=BD·CD；

(3)、【拓展提高】如图③，已知点D为Rt△ABC斜边上一点，过点D作AB的垂线，交AC于点E，点G在CE的中垂线上，连结AG，若CG= $\frac{1}{2}$ BD，求证：求证：AG＝ $\frac{1}{2}$ （AD+AB）．

查看试题解析
24. 定义：四边形ABCD中，AB=AC，∠BDC= $\frac{1}{2}$ ∠BAC，则称四边形ABCD为半角四边形，边BC称为半对边.

(1)、如图①，若四边形ABCD为半角四边形，且BC为半对边，设∠DBC=α，用含有α的代数式表示∠ACD；

(2)、如图②，等腰△ABC，AB=AC，点D为其内部一点，∠ABD=∠ACD，连结AD，作△ACD的外接圆⊙O，BD的延长线交⊙O于点E，连结EA，EC，求证：四边形ABCE为半角四边形；

(3)、如图③，在（2）的条件下，延长BA交⊙O于点F，连结EF，EF∥BC.
①求证：BC=CE；

②若AD=3，BC=6 $\sqrt{2}$ ，求四边形ADEF的面积.

查看试题解析