浙江省宁波市慈溪市2022年中考数学模拟卷
试卷更新日期:2022-04-26 类型:中考模拟
一、选择题(每小题4分,共40分)
-
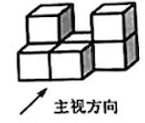
1. -3的倒数是( )A、 B、 C、-3 D、32. 据新华体育报道,国际奥委会新闻发言人在新闻发布会上透露,北京冬奥会开幕式中国大陆地区观看人数约3.16亿人. 其中3.16亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体是由7个相同的小正方体组成的立体图形, 则下列四个图形中是它的 俯视图的是( )
 A、
A、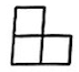 B、
B、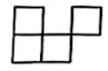 C、
C、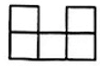 D、
D、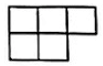 5. 不透明的袋子中装有三个小球,上面分别写着”1”, “2”, “2”, 三个小球除数字外无其他差别。从中不放回的随机摸出两个小球, 这两个小球上的数字刚好都是偶数的概率是( )A、 B、 C、 D、6. 若二次根式 在实数范围内有意义, 则下列各数中, x可取的值是( )A、4 B、 C、 D、17. 为了解邮政企业4月份收入的情况,随机抽取了25家邮政企业,获得了它们4月份收入 (单位: 百万元) 的数据, 并绘制成了频数直方图(如图, 数据分成5组: , , 现已知在这一组的数据是:. 则这25家邮政企业4月份收入的中位数是( )
5. 不透明的袋子中装有三个小球,上面分别写着”1”, “2”, “2”, 三个小球除数字外无其他差别。从中不放回的随机摸出两个小球, 这两个小球上的数字刚好都是偶数的概率是( )A、 B、 C、 D、6. 若二次根式 在实数范围内有意义, 则下列各数中, x可取的值是( )A、4 B、 C、 D、17. 为了解邮政企业4月份收入的情况,随机抽取了25家邮政企业,获得了它们4月份收入 (单位: 百万元) 的数据, 并绘制成了频数直方图(如图, 数据分成5组: , , 现已知在这一组的数据是:. 则这25家邮政企业4月份收入的中位数是( )
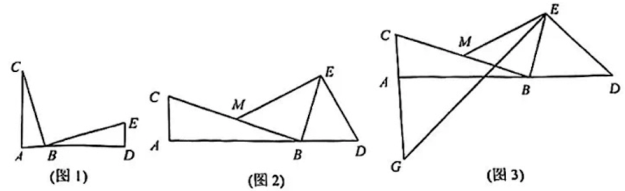
 A、10.0 B、10.1 C、10.9 D、11.58. 如图, 在中, 为边上一点, 以为圆心, 为半径的半圆切于点 , 若 , 则 的面积为( )
A、10.0 B、10.1 C、10.9 D、11.58. 如图, 在中, 为边上一点, 以为圆心, 为半径的半圆切于点 , 若 , 则 的面积为( )
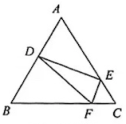
 A、 B、 C、 D、9. 当时, 二次函数的最小值为-1, 则的值为( )A、2 B、±2 C、2 或 D、2 或10. 如图, 在正中, 分别为边上的点, , 过点作 交于点 , 连结 , 若想求的周长, 则只需知道下列哪个三角形的周长? 该 三角形是( )
A、 B、 C、 D、9. 当时, 二次函数的最小值为-1, 则的值为( )A、2 B、±2 C、2 或 D、2 或10. 如图, 在正中, 分别为边上的点, , 过点作 交于点 , 连结 , 若想求的周长, 则只需知道下列哪个三角形的周长? 该 三角形是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题5 分, 共30分)
-
11. 实数9的算术平方根为.12. 因式分解: .13. 定义: [表示不大于的最大整数, 表示不小于的最小整数, 例如: , . 则.14. 我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁,母,雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡,母鸡,小鸡各多少只? 若现已知母鸡买18只, 则公鸡买只,小鸡买只。15. 如图, 中, 是的外接圆, 的延长线交边于点. 当 是等腰三角形吋, 的度数为.
 16. 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x、y轴上, 点B的坐 标为(3,1.5),反比例函数 (k为常擞, k≠0)的图象分别与边AB、BC交于点D、E,连结DE,将△BDE沿DE翻折得到△B'DE, 连结OE, 当∠OEB'=90°时,k的值为.
16. 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x、y轴上, 点B的坐 标为(3,1.5),反比例函数 (k为常擞, k≠0)的图象分别与边AB、BC交于点D、E,连结DE,将△BDE沿DE翻折得到△B'DE, 连结OE, 当∠OEB'=90°时,k的值为.

三、解答题 (本大题有8小题, 共80分)
-
17.(1)、计算: .(2)、解不等式组:18. 如图是由边长为1的小正方形构成的的网格, 点均在格点上.
 (1)、在图1中画出以为对角线的正方形 , 点为格点.(2)、在图2中画出以为边且周长最大的平行四边形 , 点为格点 (画一个即可).19. “千年越窑,秘色慈溪”,为了解学生对慈溪秘色瓷的熟悉度,某校设置了非常了解,基本了解,很少了解,不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成如下不完整的统计图。
(1)、在图1中画出以为对角线的正方形 , 点为格点.(2)、在图2中画出以为边且周长最大的平行四边形 , 点为格点 (画一个即可).19. “千年越窑,秘色慈溪”,为了解学生对慈溪秘色瓷的熟悉度,某校设置了非常了解,基本了解,很少了解,不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成如下不完整的统计图。

根据图中信息, 解答下列问题:
(1)、 本次接受问卷调查的学生有多少人?(2)、 求图2中 “很少了解” 的扇形圆心角的度数.(3)、全校共有960名学生, 请你估计全校学生中“非常了解”秘色瓷的学生共有多少人?20. 如图, 在平面直角坐标系中, 直线与轴、 轴分别交于 两点. 抛物线经过点 , 且交线段于点. (1)、 求k的值.(2)、 求点c的坐标.(3)、向左平移抛物线, 使得抛物线再次经过点 , 求平移后抛物线的函数解析式.21. 图1为科研小组研制的智能机器,水平操作台为 , 底座AB固定,高AB为 , 始终与平台垂直, 连杆长度为 , 机械臂长度为 , 点 是转动点,与始终在同一平面内, 张角可在与之间 (可以达到 和)变化, 可以绕点任意转动.
(1)、 求k的值.(2)、 求点c的坐标.(3)、向左平移抛物线, 使得抛物线再次经过点 , 求平移后抛物线的函数解析式.21. 图1为科研小组研制的智能机器,水平操作台为 , 底座AB固定,高AB为 , 始终与平台垂直, 连杆长度为 , 机械臂长度为 , 点 是转动点,与始终在同一平面内, 张角可在与之间 (可以达到 和)变化, 可以绕点任意转动. (1)、转动连杆 , 机械 , 使张角最大, 且 , 如图2,求机械臂臂端D 到操作台1的距离DE的长.(2)、转动连杆 , 机械臂机械臂端能碰到操作台1上的物体M,则物体M离底座的最远距离和最近距离分别是多少?22. 甲、乙两人沿同一路线从地到地进行骑车训练, 甲先出发, 匀速骑行到地. 乙后出发,并在甲骑行25分钟后提速到原来速度的1.4倍继续骑行(提速过程的时间忽略不计), 结果乙比甲早12分钟到地. 两人距离地的路程 (单位: 千米) 与甲骑行的时间 (单位:分钟)之间的关系如图所示.
(1)、转动连杆 , 机械 , 使张角最大, 且 , 如图2,求机械臂臂端D 到操作台1的距离DE的长.(2)、转动连杆 , 机械臂机械臂端能碰到操作台1上的物体M,则物体M离底座的最远距离和最近距离分别是多少?22. 甲、乙两人沿同一路线从地到地进行骑车训练, 甲先出发, 匀速骑行到地. 乙后出发,并在甲骑行25分钟后提速到原来速度的1.4倍继续骑行(提速过程的时间忽略不计), 结果乙比甲早12分钟到地. 两人距离地的路程 (单位: 千米) 与甲骑行的时间 (单位:分钟)之间的关系如图所示. (1)、求甲的速度和乙提速前的速度.(2)、求两地之间的路程.
(1)、求甲的速度和乙提速前的速度.(2)、求两地之间的路程.