云南省文山州砚山县2022年初中学业水平模拟考试一模数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数中，最小的数是（）

A、 $| - 2 |$ B、0 C、 ${(- 1)}^{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 如图，直线 $a ∥ b$ ，则∠1与∠2和的一半是（）

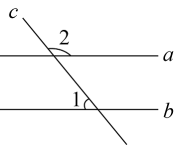A、45° B、50° C、90° D、180°

查看试题解析
3. 下列运算中，正确的是（）

A、 $\sqrt[3]{- 8} = 2$ B、 $x^{8} \div x^{4} = x^{2}$ C、 $| 2 - \sqrt{3} | = 2 - \sqrt{3}$ D、 ${(x - 2)}^{2} = x^{2} - 4$

查看试题解析
4. 已知一个三角形的三条边长都是2，则该三角形的面积为（）

A、 $\sqrt{3}$ B、 $\frac{4 \sqrt{3}}{3}$ C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
5. 最小刻度为 $0.2 n m (l n m = 1 0^{- 9} m)$ 的钻石标尺，可以测量的距离小到不足头发丝直径的十万分之一，这也是目前世界上刻度最小的标尺，用科学记数法表示这一最小刻度为（）

A、 $2 \times 1 0^{- 8} m$ B、 $0.2 \times 1 0^{- 9} m$ C、 $2 \times 1 0^{- 9} m$ D、 $2 \times 1 0^{- 10} m$

查看试题解析
6. 如图，在 $△ A B C$ 中，点D、E、F分别是AB、BC、AC的中点，则下列四个判断中，不正确的是（）

A、四边形ADEF是平行四边形 B、若 $∠ A = 90 °$ ，则四边形ADEF是矩形 C、若 $A B = A C$ ，则四边形ADEF是菱形 D、若四边形ADEF是正方形，则 $△ A B C$ 是等边三角形

查看试题解析
7. 已知点 $(2 ， - 2)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，则下列各点在该函数图象上的是（）

A、 $(- 4 ， 1)$ B、 $(1 ， 4)$ C、 $(- 2 ， - 2)$ D、 $(4 ， - \frac{1}{2})$

查看试题解析
8. 如果多项式 $a x + b$ 与 $2 x + 1$ 的乘积展开式中不含x的一次项，且常数项为6，则 $a + b$ 的值为（）

A、-12 B、-6 C、6 D、18

查看试题解析
9. 如图，AB是⊙O的直径，CD垂直平分OB交⊙O于C、D两点， $∠ A B C = 60 °$ ， $C D = 2 \sqrt{3}$ ，则图中阴影部分的面积为（）

A、 $\frac{2}{3} π$ B、 $π$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
10. 下列说法中，不正确的是（）

A、买一张彩票会中奖是随机事件 B、为了了解全校学生的视力情况，可以采用抽样调查的方式 C、比赛中“去掉一个最高分，去掉一个最低分”后，众数一定不会发生变化 D、甲、乙两人进行射击测试，每人10次射击成绩的平均数均是9环，方差分别为 ${S_{甲}}^{2} = 0.68$ ， ${S_{乙}}^{2} = 0.54$ ，则乙的成绩比甲的成绩更稳定

查看试题解析
11. 如图是一个几何体的三视图，根据图中提供的数据，计算这个几何体的表面积是（）

A、 $32 π$ B、 $48 π$ C、 $64 π$ D、 $80 π$

查看试题解析
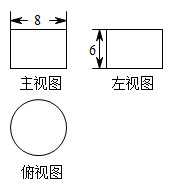12. 若关于x的一元一次不等式组 ${\begin{array}{l} 2 (x + 1) < x + 3 \\ x - a \leq 2 \end{array}$ 的解集是 $x < 1$ ；关于x的分式方程 $\frac{x + a}{x - 2} + \frac{2 a}{2 - x} = 2$ 的解为非负整数，则满足条件的整数a的值之和是（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

13. 二次根式 $\sqrt{x + 3}$ 中，x的取值范围是 .

查看试题解析
14. 一个多边形的内角和是1080°则这个多边形的边数是．

查看试题解析
15. 已知关于x的一元二次方程x²﹣2kx＋k²＋k﹣2＝0有两个不相等的实数根，则k的最大整数值是．

查看试题解析
16. 如图，在 $▱ A B C D$ 中，对角线AC、BD相交于点O， $∠ B A C = 90 °$ ， $A D = 15$ ， $O C = 6$ ，则 $△ B O C$ 的面积为．

查看试题解析
17. 如图是一组有规律的图案，它们是由边长相等的等边三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形…照此规律摆下去，摆成第2022个图案需要个三角形．

查看试题解析
18. 如图，Rt△ABC中，∠ACB＝90°，CD⊥AB，AC＝5，BC＝12，点P是线段CD上一动点，当半径为4的⊙P与△ABC的一边相切时，CP的长为.

查看试题解析

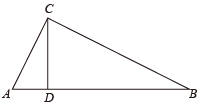
三、解答题

19. 某校为了提高学生学习安全知识的积极性，举办了“安全第一”知识大赛，该校所有学生均参加初赛．初赛中，将安全知识设置为100分试卷，学生的分数均在50分以上，为了解学生对安全知识的掌握情况，学校随机抽取一部分学生的成绩进行统计分析，绘制了如下统计图表：
成绩x（分）
频数（人）
频率
$50 < x < 60$
2
0.04
$60 \leq x < 70$
10
0.2
$70 \leq x < 80$
14
b
$80 \leq x < 90$
a
0.32
$90 \leq x \leq 100$
8
0.16
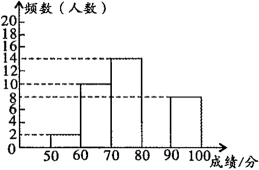
请根据统计图表提供的信息，解答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、 $a =$ ； $b =$ ；

(3)、补全频数分布直方图；

(4)、若该校有2800名学生，初赛成绩不低于80分为优秀，则本次初赛达到优秀的学生大约有多少人？

查看试题解析
20. 扑克牌在生活中很常见，扑克牌的设计和发明与天文、历法有着千丝万缕的联系．一副扑克牌共有54张：大王代表太阳、小王代表月亮，其余52张牌代表一年中的52个星期；红桃、方块、梅花、黑桃四种花色分别象征着春、夏、秋、冬四个季节；每种花色13张牌，表示每个季节有13个星期；如果把J、Q、K分别当作11、12、13点，大王、小王为半点，一副扑克牌的总点数恰好是365点，而闰年把大、小王各算为1个点，共366点．小明将黑桃A、红桃2、梅花3、方块4这四张牌背面朝上放置在桌面上，洗匀后从中任意翻开两张．

(1)、用列表或画树状图的方法表示出所有可能出现的结果；

(2)、求翻开的两种扑克牌分别表示冬季、春季的概率．

查看试题解析
21. 某学校管理委员会要添置A、B两种型号的办公桌共20套，已知购买2套A型办公桌和1套B型办公桌共需1000元，1套A型办公桌和3套B型办公桌共需1500元．

(1)、求A、B两种型号的办公桌每套各是多少元？

(2)、若管理委员会需要A型办公桌不少于12套，B型办公桌不少于6套，平均每套办公桌需要运费20元．设购买A型办公桌x套，总费用为y元．
①求y与x之间的函数关系式；
②求出总费用最少的购买方案．

查看试题解析
22. 如图，在矩形ABCD中，E是AD的中点，将 $△ A B E$ 沿BE折叠后得到 $△ G B E$ ，且G点在矩形ABCD的内部，延长BG交DC于点F，连接EF．

(1)、求证： $△ D E F ≌ △ G E F$ ；

(2)、若 $D C ： D F = 3 ： 2$ ，求 $\frac{A D^{2}}{A B^{2}}$ 的值．

查看试题解析
23. 已知抛物线 $y = x^{2} - a x - x + a (a > 1)$ 与x轴交于A、B两点，点A在点B的左侧，且 $O B = 3 O A$ ．

(1)、求A、B两点的坐标；

(2)、已知点M是抛物线上一点，且纵坐标为m，若n满足 $n + m^{2} + 10 m = 0$ ，求n的最大值．

查看试题解析
24. 如图， $△ A B C$ 是⊙O的内接三角形， $A D ⊥ B C$ 于点D，直径AE平分∠BAD，交BC于点F，连接BE．

(1)、求证： $∠ A E B = ∠ A F D$ ；

(2)、若 $A B = 10$ ， $B F = 5$ ，求AD的长；

(3)、若点G是AB的中点，当点O在DG上时，探究BF与FD存在的数量关系，并说明理由．

查看试题解析

成绩x（分）	频数（人）	频率
$50 < x < 60$	2	0.04
$60 \leq x < 70$	10	0.2
$70 \leq x < 80$	14	b
$80 \leq x < 90$	a	0.32
$90 \leq x \leq 100$	8	0.16