云南省文山州丘北县2022年中考数学一模试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，点O在直线AB上，若∠AOC=60°，则∠BOC的大小是（）

A、 $60 °$ B、 $90 °$ C、 $120 °$ D、 $150 °$

查看试题解析
2. 若 $\sqrt{2 x + 1}$ 有意义，则（）

A、 $x \geq - \frac{1}{2}$ B、 $x > - \frac{1}{2}$ C、 $x \neq \frac{1}{2}$ D、 $x \geq \frac{1}{2}$

查看试题解析
3. 如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 地球距离太阳约为150000000千米，这个距离用科学记数法表示为（）

A、 $1.5 \times 10^{7}$ 千米 B、 $1.5 \times 10^{8}$ 千米 C、 $0.15 \times 10^{9}$ 千米 D、 $15 \times 10^{7}$ 千米

查看试题解析
5. 关于x的一元二次方程 $x^{2} - 4 x + k = 0$ 的一个根是1，则另一个根是（）

A、3 B、－2 C、－3 D、－4

查看试题解析
6. 一个多边形的内角和为1260°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、多边形

查看试题解析
7. 下列运算中，正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $(2 - \sqrt{3})^{0} = 1$ C、a²+2a³＝2a⁵ D、（﹣2a²）³＝﹣6a⁶

查看试题解析
8. 如图，在△ABC中，AD⊥BC于点D，CE⊥AB于点E，AD、CE交于点F，已知EF＝EB＝3，S_△AEF＝6，则CF的长为（）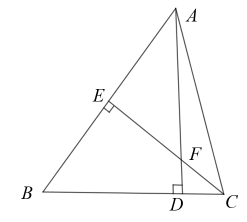

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
9. 按一定规律排列的单项式：﹣a，4a² ， ﹣9a³ ， 16a⁴ ， ﹣25a⁵ ， ⋯⋯，则第n个单项式为（）

A、（﹣n）²aⁿ B、（﹣1）ⁿ2ⁿaⁿ C、（﹣1）ⁿn²aⁿ D、（﹣1）ⁿ⁺¹n²aⁿ⁺¹

查看试题解析
10. 随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，平均每人每天比原来多投递5件，公司投递快件的能力由每天320件提高到480件，若快递公司的快递员人数不变，求原来平均每人每天投递快件多少件？设原来平均每人每天投递快件x件，根据题意可列方程为（）

A、 $\frac{320}{x} = \frac{480}{x - 5}$ B、 $\frac{320}{x} = \frac{480}{x + 5}$ C、 $\frac{480}{x} = \frac{320}{x} - 5$ D、 $\frac{320}{x} + 5 = \frac{480}{x}$

查看试题解析
11. 某公司今年1～4月的电子产品销售总额如图1所示，其中平板电脑的销售额占当月电子产品销售总额的百分比如图2，据图中信息，得到的结论不合理的是（）

A、这4个月，电子产品销售总额为290万元 B、平板电脑销售额占当月电子产品销售总额的百分比，1月最高 C、这4个月，平板电脑销售额最低的是3月 D、平板电脑4月份的销售额比3月份有所下降

查看试题解析
12. 如图，BC是⊙O的直径，点A是⊙O上的一点，点D是△ABC的内心，若BC＝5，AC＝3，则BD的长度为（）

A、2 B、3 C、 $\sqrt{10}$ D、 $\frac{\sqrt{34}}{2}$

查看试题解析

二、填空题

13. 某日的最低气温为−2℃，最高气温比最低气温高6℃，则这一天的最高气温是．

查看试题解析
14. 因式分解：x²﹣4= ．

查看试题解析
15. 在△ABC中，D、E分别是AB、AC的中点，DE＝4，则BC＝．

查看试题解析
16. 已知点P在双曲线 $y = \frac{6}{x}$ 的图象上，PA⊥x轴于点A，O为坐标原点，则△OPA的面积为．

查看试题解析
17. 一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图扇形的圆心角是．

查看试题解析
18. 正方形ABCD的边长为8，点E在BC边上，且CE＝2，点P是正方形边上的一个动点，连接PB交AE于点F，若PB＝AE，则PF的长为．

查看试题解析

三、解答题

19. 某校为了了解九年级学生在寒假期间的数学学习情况，开学之际进行了一次数学小测验（满分100分），并从甲、乙两个班各抽取10名学生的测验成绩进行统计分析．
收集数据：
甲班：90，90，70，90，100，80，80，90，95，65
乙班：95，70，80，90，70，80，95，80，100，90
整理数据
成绩x（分）
60≤x≤70
70＜x≤80
80＜x≤90
90＜x≤100
甲班
2
2
4
2
乙班
2
3
a
3
分析数据
数据
平均数
中位数
众数
甲班
85
90
d
乙班
b
c
80

(1)、直接写出a、b、c、d的值；

(2)、小明同学说：“这次测验我得了90分，在我们小组中属于中游偏上！”观察上面的表格判断，小明可能是班的学生；

(3)、若乙班共有50人参加测验，请估计乙班测验成绩超过90分的人数．

查看试题解析
20. 某学校为了迎接国家文明城市的复查，需要选取1名或2名同学作为志愿者.九（1）班的A同学、B同学和九（2）班的C同学、D同学4名同学报名参加.

(1)、若从这4名同学中随机选取1名志愿者，则被选中的这名同学恰好是九（1）班同学的概率是.

(2)、若从这4名同学中随机选取2名志愿者，请用列举法（画树状图或列表）求这2名同学恰好都是九（2）班同学的概率.

查看试题解析
21. 如图，四边形ABCD是矩形，点E、F分别在边AD、BC上，将矩形ABCD沿EF对折，点B与点D恰好重合．

(1)、求证：四边形BEDF是菱形；

(2)、若AB＝6，BC＝8，求折痕EF的长．

查看试题解析
22. 某通讯公司推出了两种上网流量的收费方式供用户选择：
方案一：套餐费+流量费；

方案二：仅收流量费，无套餐费．

如图中的射线l₁ ，射线l₂分别表示通讯公司每月按方案一，方案二收取的流量费y₁（元）和y₂（元）与当月用户使用流量x（G）的函数关系．

(1)、分别求出y₁、y₂与x的函数表达式；

(2)、若某用户今年2月份已使用流量少于10G，但其2月份的流量费超过40元，那么该用户采用了哪种方案支付上网流量？

查看试题解析
23. 如图，在Rt△ADE中，∠ADE＝90°，点O是AE上一点，以O为圆心，OA长为半径的圆与DE相切于点C，与AE相交于点B．

(1)、求证：AC平分∠DAE；

(2)、若AD＝6，CD＝2 $\sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析
24. 如图，已知抛物线 $y = \frac{1}{3} x^{2} + b x + c$ 经过△ABC的三个顶点，其中点A（0，1），点B（－9，10），AC∥x轴，点P是直线AC下方抛物线上的一个动点．

(1)、求抛物线的解析式．

(2)、过点P与y轴平行的直线l与直线AB，AC分别交于点E，F，当点P在何处时，四边形AECP的面积最大，最大是多少？

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C，P，Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

成绩x（分）	60≤x≤70	70＜x≤80	80＜x≤90	90＜x≤100
甲班	2	2	4	2
乙班	2	3	a	3

数据	平均数	中位数	众数
甲班	85	90	d
乙班	b	c	80