云南省曲靖市罗平县2022年中考一模数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年春季开学后，罗平县遇到天气突然降温，2月22日的最高气温是 $3 ℃$ ，最低气温是 $- 2 ℃$ ，那么这天的温差是（）

A、 $5 ℃$ B、 $- 5 ℃$ C、 $1 ℃$ D、 $- 1 ℃$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，把一块直角三角尺的直角顶点放在直尺的一边上，若 $∠ 1 = 55 °$ ，则 $∠ 2$ 的度数为（）

A、 $55 °$ B、 $45 °$ C、 $35 °$ D、 $25 °$

查看试题解析
4. 若一个多边形的每个外角都是60°，则这个多边形的内角和是（）．

A、540° B、720° C、900° D、1080°

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $5 x^{3}$ - $3 x^{2}$ =2x C、 $(a + b)^{2} = a^{2} + a b + b^{2}$ D、 $(- a b)^{3} = - a^{3} b^{3}$

查看试题解析
6. 如图，点 $D$ 、 $E$ 分别是 $△ A B C$ 边 $B A$ 、 $B C$ 的中点， $△ A B C$ 的面积等于 $8$ ，则 $△ B D E$ 的面积为（）

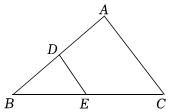A、2 B、3 C、4 D、5

查看试题解析
7. 《九章算术》是中国传统数学的重要著作，方程术是它的最高成就．其中记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出 $8$ 钱，会多 $3$ 钱；每人出 $7$ 钱，又会差 $4$ 钱，问人数、物价各是多少？设合伙人数为 $x$ 人，物价为 $y$ 钱，以下列出的方程组正确的是（）

A、 ${\begin{matrix} y - 8 x = 3 \\ y - 7 x = 4 \end{matrix}$ B、 ${\begin{matrix} y - 8 x = 3 \\ 7 x - y = 4 \end{matrix}$ C、 ${\begin{matrix} 8 x - y = 3 \\ y - 7 x = 4 \end{matrix}$ D、 ${\begin{matrix} 8 x - y = 3 \\ 7 x - y = 4 \end{matrix}$

查看试题解析
8. 如图，Rt△ABC中，∠ACB＝90°，AB＝5，AC＝4，CD⊥AB于D，则tan∠BCD的值为（）

A、 $\frac{4}{5}$ B、 $\frac{5}{4}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

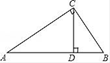查看试题解析
9. 下列说法正确的是（）

A、为了加强“五项管理”，要了解某市中学生的睡眠时间，采用全面调查 B、打开电视机，它正在播广告是必然事件 C、一组数据“ $5$ ， $4$ ， $6$ ， $2$ ， $7$ ， $4$ ， $3$ ”的众数是 $4$ ，中位数是 $2$ D、甲、乙两名同学 $5$ 次数学测试的平均分都是 $92$ 分，方差分别为 $S_{甲}^{2} = 0.8$ ， $S_{乙}^{2} = 1.2$ ，由此可以判断甲的数学成绩比乙的稳定

查看试题解析
10. 已知关于 $x$ 的一元二次方程 $(1 - a) x^{2} + 2 x - 2 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是（）

A、 $a < \frac{3}{2}$ B、 $a > \frac{1}{2}$ C、 $a < \frac{3}{2}$ 且 $a \neq 1$ D、 $a > \frac{1}{2}$ 且 $a \neq 1$

查看试题解析
11. 有一列按一定规律排列的式子：﹣3m，9m，﹣27m，81m，﹣243m，…，则第n个式子是（）

A、（﹣3）ⁿm B、（﹣3）ⁿ⁺¹m C、3ⁿm D、﹣3ⁿm

查看试题解析
12. 如图所示，二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (- 3 ， 0)$ ，其对称轴为直线 $x = - 1$ ，有下列结论：① $a b c < 0$ ；② $a + b + c < 0$ ；③ $2 a - b = 0$ ；④ $4 a c - b^{2} > 0$ ；⑤当 $x < - 3$ 时， $y > 0$ ．其中正确结论的个数是（）

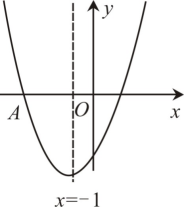A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算： $(﹣ 1)^{2} + 2 c o s 60 ° + 2^{﹣ 2} - (π - 2022)^{0}$ 的值是．

查看试题解析
14. 若点 $A (x ， y)$ 在反比例函数 $y = \frac{4}{x}$ 的图象上，则代数式xy的值为．

查看试题解析
15. 分解因式： $3 x^{2} - 27$ = ．

查看试题解析
16. 若实数 $m$ ， $n$ 满足 $| m - 2 | + \sqrt{n - 4} = 0$ ，则 $n^{m} =$ ．

查看试题解析
17. 如图，在平面直角坐标系中，A（3，0），B（0，4），连接AB，在平面直角坐标系中找一点C，使△AOC与△AOB全等，则C点的坐标为
.

查看试题解析
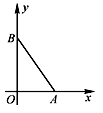18. 如图，在边长为2的正方形ABCD中，对角线AC的中点为O，分别以点A，C为圆心，以AO的长为半径画弧，分别与正方形的边相交，则图中的阴影部分的面积为.（结果保留π）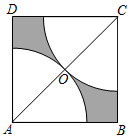

查看试题解析

三、解答题

19. 2021年4月25日，教育部办公厅印发了 $《$ 关于加强义务教育学校作业管理的通知 $》 ($ 以下简称 $《$ 通知 $》) . 《$ 通知 $》$ 强调要严格控制书面作业总量，要求小学一二年级不布置书面家庭作业，小学其他年级每天书面作业完成时间平均不超过60分钟；初中不超过90分钟．同时， $《$ 通知 $》$ 明确提出不得要求学生自批自改，严禁给家长布置或变相布置作业，严禁要求家长批改作业，让作业回归到学校育人环节中来．有条件的地方，鼓励科学利用信息技术手段进行作业分析诊断．某校对八年级学生每天完成数学作业时间调查如下，按照完成时间分为： $A$ “15分钟”、 $B$ “20分钟”、 $C$ “25分钟”、 $D$ “30分钟”、 $E$ “35分钟” $.$ 为了了解学生对课外数学作业的完成情况，随机抽取了部分同学进行调查，将调查结果绘制成如图两幅不完整的统计图．

根据以上信息，回答下列问题：

(1)、统计图中的 $a =$ ， $b =$ ；

(2)、该校八年级共有600名学生，请你估计该校八年级学生能在20分钟内完成数学作业的学生人数．

(3)、为了学生各学科之间均衡发展，你认为该校八年级布置的数学课外作业是否合理？若合理，请你说明理由．若不合理，请你设计出合理化的布置方案．

查看试题解析
20. 到2023年云南省率先实现体育中考改革，把体育与语、数、英并列，按100分计入升学总分，每学期进行一次体育测试，现有四张分别标有数字和球类的卡片，1足球、2篮球、3排球、4乓球，将4张卡片洗匀后背面朝上．

(1)、若小宇从中任意抽取1张，抽到篮球测试的概率是；

(2)、若小宇先从中任意抽取 $1$ 张 $($ 不放回 $)$ ，再从余下的 $3$ 张中任意抽取1张，求两次抽到篮球和排球测试的概率 $. ($ 请用“画树状图”或“列表”等方法写出分析过程 $)$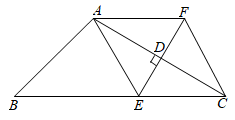

查看试题解析
21. 如图，已知 $△ A B C$ 中，D是 $A C$ 的中点，过点D作 $D E ⊥ A C$ 交 $B C$ 于点E，过点A作 $A F / / B C$ 交 $D E$ 于点F，连接 $A E$ 、 $C F$ .

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $C F = 2 ， ∠ F A C = 30 ° ， ∠ B = 45 °$ ，求 $A B$ 的长.

查看试题解析
22. 罗平县小黄姜生产销售扶贫公司，2021年生产并销售小黄姜情况如图．该公司销售量与生产量相等，图中的折线 $A B D$ 、线段 $C D$ 分别表示该产品每千克生产成本 $y_{1} ($ 单位：万元 $)$ 、销售价 $y_{2} ($ 单位：万元 $)$ 与产量 $x ($ 单位：吨 $)$ 之间的函数关系．

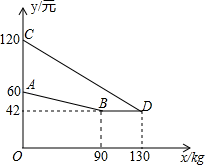(1)、求该产品每千克生产成本 $y_{1}$ 与 $x$ 之间的函数关系式；

(2)、当该产品产量为多少时，获得的利润最大？最大利润是多少？

查看试题解析
23. 如图，已知 $C D$ 是 $⊙ O$ 的直径， $A E$ 是 $⊙ O$ 的切线，切点为 $E$ 点．弦 $D E / / O A$ ，直线 $A E$ 、 $C D$ 相交于点 $B$ ．

(1)、求证：直线 $A C$ 是 $⊙ O$ 的切线；

(2)、若 $A E$ ： $B E = 1$ ： $2$ ，求 $s i n ∠ O A C$ 的值．

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴相交于点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，与 $y$ 轴的交点 $C (0 ， 6)$ ．

(1)、求抛物线的解析式；

(2)、点 $P (m ， n)$ 在平面直角坐标系第一象限内的抛物线上运动，设 $△ P B C$ 的面积为S，求S关于 $m$ 的函数表达式 $($ 指出自变量 $m$ 的取值范围 $)$ 和S的最大值；

(3)、点 $M$ 在抛物线上运动，点 $N$ 在 $y$ 轴上运动，是否存在点 $M$ 、点 $N$ 使得∠CMN＝90°，且 $Δ C M N$ 与 $Δ O B C$ 相似，如果存在，请求出点 $M$ 和点 $N$ 的坐标．

查看试题解析