云南省禄劝彝族苗族自治县2022年初中学业水平模拟考试数学试题（一）

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是某几何体的展开图，该几何体是（）

A、长方体 B、球体 C、圆锥 D、圆柱

查看试题解析
2. 在函数 $y = \frac{2}{3 x - 1}$ 中x的取值范围是（）

A、 $x > \frac{1}{3}$ B、 $x < \frac{1}{3}$ C、 $x \neq \frac{1}{3}$ D、 $x \neq - \frac{1}{3}$

查看试题解析
3. 如图，直线a∥b，直线 $c$ 分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是（）

A、50° B、70° C、80° D、110°

查看试题解析
4. 2022年初，根据当地疫情防控要求，从省外返回的人员原则上需要自行居家观察14天，减少外出活动.14天的时间有1209600秒，1209600用科学记数法表示为（）

A、 $0.12096 \times 1 0^{7}$ B、 $1.2096 \times 1 0^{6}$ C、 $1.2096 \times 1 0^{- 6}$ D、 $12.096 \times 1 0^{5}$

查看试题解析
5. 下列运算正确的是（）

A、 $| \sqrt{3} - 2 | = \sqrt{3} - 2$ B、 $2^{- 2} = - 4$ C、 ${(- 3)}^{0} = 0$ D、 $3 < x < 3 \sqrt{2} + 3$

查看试题解析
6. 如图，在 $∠ A O B$ 中，尺规作图如下：在射线 $O A$ 、 $O B$ 上，分别截取 $O D$ 、 $O E$ ，使 $O D = O E$ ；分别以点 $D$ 和点 $E$ 为圆心、大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧相交于点 $C$ ；作射线 $O C$ ，连结 $C E$ 、 $C D$ .下列结论不一定成立的是（）

A、 $O E = E C$ B、 $C E = C D$ C、 $∠ O E C = ∠ O D C$ D、 $∠ E C O = ∠ D C O$

查看试题解析
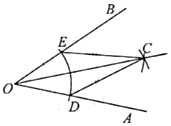7. 关于x的一元二次方程 $a x^{2} - 3 x + 1 = 0$ 有实数根，则a的取值范围是（）

A、 $a < \frac{9}{4}$ 且 $a \neq 0$ B、 $a \leq \frac{9}{4}$ 且 $a \neq 0$ C、 $a \leq \frac{9}{4}$ D、 $a < \frac{9}{4}$

查看试题解析
8. 5月1日至7日，我市每日最高气温如图所示，则下列说法不正确的是（）

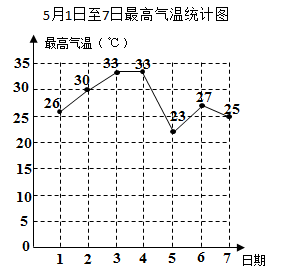A、中位数是 $33 ° C$ B、众数是 $33 ° C$ C、平均数是 $\frac{197}{7} ° C$ D、4日至5日最高气温下降幅度较大

查看试题解析
9. 为迎接建党一百周年，某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威，其中荧光棒共花费40元，缤纷棒共花费30元，缤纷棒比荧光棒少20根，缤纷棒单价是荧光棒的1.5倍．若设荧光棒的单价为 $x$ 元（）

A、 $\frac{40}{1.5 x} - \frac{30}{x} = 20$ B、 $\frac{40}{x} - \frac{30}{1.5 x} = 20$ C、 $\frac{30}{x} - \frac{40}{1.5 x} = 20$ D、 $\frac{30}{1.5 x} - \frac{40}{x} = 20$

查看试题解析
10. 小丽利用学习的数学知识，给同伴出了这样一道题：假如从点A出发，如图所示，沿直线走6米后向左转 $θ$ ，接着沿直线前进6米后，再向左转 $θ$ ……如此走法，当她第一次走到A点时，发现自己走了72米， $θ$ 的度数为（）

A、30° B、32° C、35° D、36°

查看试题解析
11. 已知 $4 3^{2} = 1849$ ， $4 4^{2} = 1936$ ， $4 5^{2} = 2025$ ， $4 6^{2} = 2116$ ．若n为整数且 $n - 1 < \sqrt{2022} < n$ ，则n的值为（）

A、43 B、44 C、45 D、46

查看试题解析
12. 若整数a使得关于x的分式方程 $\frac{x}{x - 2} + \frac{a + 1}{2 - x} = 2$ 解的取值范围为 $0 \leq x \leq 3$ ，则符合条件的a值可以为（）

A、5 B、4 C、1 D、0

查看试题解析

二、填空题

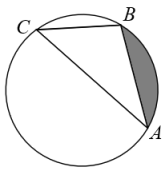
13. 计算：2sin60°= ．

查看试题解析
14. 分解因式： $5 x^{2} - 5 y^{2} =$ ．

查看试题解析
15. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (1 ， 2)$ 和点 $B (- 1 ， m)$ ，则 $m$ 的值为．

查看试题解析
16. 观察下列等式： $1 = 1^{2} - 0^{2}$ ， $3 = 2^{2} - 1^{2}$ ， $5 = 3^{2} - 2^{2}$ ， …按此规律，则第8个等式为．

查看试题解析
17. 如图，点A，B，C，在半径为6的圆上，∠ACB=45°，则图中阴影部分的面积为（结果保留 $π$ ）．

查看试题解析
18. 如图，在等腰三角形纸片ABC中，AB=AC=10，BC=12，沿底边BC上的高AD剪成两个三角形，用这两个三角形拼成平行四边形，则这个平行四边形较长的对角线的长是．

查看试题解析

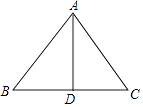
三、解答题

19. 为了提高学生的综合素养，某校开设了五门手工活动课．按照类别分为：A“剪纸”、B“沙画”、C“葫芦雕刻”、D“泥塑”、E“插花”．为了了解学生对每种活动课的喜爱情况，随机抽取了部分同学进行调查，将调查结果绘制成如下两幅不完整的统计图．

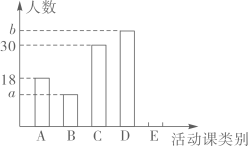
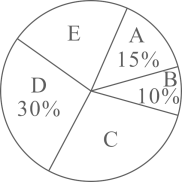
根据以上信息，回答下列问题：

(1)、本次调查的样本容量为；统计图中的 $a =$ ， $b =$ ；

(2)、通过计算补全条形统计图；

(3)、该校共有2500名学生，请你估计全校喜爱“葫芦雕刻”的学生人数．

查看试题解析
20. 四张正面分别写有数字： $- 2$ ， $- 1$ ， 0，1的卡片，它们的背面完全相同，现将这四张卡片背面朝上洗匀．

(1)、从中任意抽取一张卡片则所抽卡片上数字为负数的概率是；

(2)、先从中任意抽取一张卡片，以其正面数字作为x的值，然后再从剩余的卡片中随机抽一张，以其正面的数字作为y的值，请用列表法或树状图法．求点 $P (x ， y)$ 在坐标轴上的概率．

查看试题解析
21. 甲、乙两人沿同一直道从A地去B地.已知A，B两地相距9000m，甲的步行速度为100m/min，他每走半个小时就休息15min，经过2小时到达目的地.乙的步行速度始终不变，他在途中不休息，在整个行程中，甲离A地的距离 $y_{1}$ （单位：m）与时间x（单位：min）之间的函数关系如图所示（甲、乙同时出发，且同时到达目的地）.

(1)、在图中画出乙离A地的距离 $y_{2}$ （单位：m）与时间x之间的函数图象；

(2)、求甲、乙两人在途中相遇的时间.

查看试题解析
22. 已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作 $D E ⊥ M N$ 于E．

(1)、求证：DE是⊙O的切线；

(2)、若 $t a n ∠ D A E = 2$ ，四边形ACDE的面积为6，求⊙O的半径．

查看试题解析
23. 已知抛物线 $y = a x^{2} - 2 x + c$ 与x轴只有一个交点 $(1 ， 0)$ ，并且还经过 $(2 ， - 1)$ ， $(0 ， 1)$ 两点中的一个点．

(1)、求抛物线的解析式；

(2)、设直线 $y = n (n > 0)$ 与抛物线交于点A，B，与抛物线 $y = \frac{1}{2} {(x - 1)}^{2}$ 交于点C，D，说明线段AB与线段CD之间的数量关系．

查看试题解析
24. 如图，现有一张矩形纸片ABCD，AB＝4，BC＝8，点M，N分别在矩形的边AD，BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN丁点Q，连接CM．

(1)、求证：PM＝PN；

(2)、当P，A重合时，求MN的值；

(3)、若△PQM的面积为S，求S的取值范围．

查看试题解析