云南省昆明市呈贡区2022年初中学业水平第一次模拟考试数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
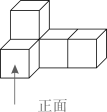
1. 如果规定收入为正,支出为负,收入3元记作3元,那么支出8元记作( )A、5元 B、-11元 C、11元 D、-8元2. 如图是由5个相同的小正方体组成的几何体,该几何题的左视图是( )
 A、
A、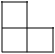 B、
B、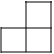 C、
C、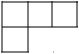 D、
D、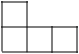 3. 一个多边形内角和等于1080°,则这个多边形的边数是( )A、6 B、8 C、10 D、124. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、要了解昆明市九年级学生的视力情况应采用全面调查 B、2022年春节期间,随机走进一家电影厅,正在播放电影《狙击手》是必然事件 C、一组数据12,24,24,35, , 43中,第五个数的个位数字被墨水涂污,则统计分析结果与被涂污数字无关的是众数 D、甲乙两组数据平均数均为0.5,方差分别为 , , 则甲组数据的波动程度较大6. 在△ABC中,∠C=90°,若AC=1,BC=3,则sinB的值为)( )A、 B、 C、 D、37. 已知关于x的一元二次方程根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数报8. 如图,O是矩形的对角线的中点,M是的中点,若 , , 则四边形的周长为( )
3. 一个多边形内角和等于1080°,则这个多边形的边数是( )A、6 B、8 C、10 D、124. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、要了解昆明市九年级学生的视力情况应采用全面调查 B、2022年春节期间,随机走进一家电影厅,正在播放电影《狙击手》是必然事件 C、一组数据12,24,24,35, , 43中,第五个数的个位数字被墨水涂污,则统计分析结果与被涂污数字无关的是众数 D、甲乙两组数据平均数均为0.5,方差分别为 , , 则甲组数据的波动程度较大6. 在△ABC中,∠C=90°,若AC=1,BC=3,则sinB的值为)( )A、 B、 C、 D、37. 已知关于x的一元二次方程根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数报8. 如图,O是矩形的对角线的中点,M是的中点,若 , , 则四边形的周长为( ) A、18 B、16 C、19 D、209. 若点 , , 都在反比例函数的图象上,且 , 则 , , 的大小关系是( )A、 B、 C、 D、10. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、11. 如图,将边长为1的菱形绕点A旋转,当B,C两点恰好落在扇形的上时,的长度等于( )
A、18 B、16 C、19 D、209. 若点 , , 都在反比例函数的图象上,且 , 则 , , 的大小关系是( )A、 B、 C、 D、10. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、11. 如图,将边长为1的菱形绕点A旋转,当B,C两点恰好落在扇形的上时,的长度等于( ) A、 B、 C、 D、12. 如图,抛物线的顶点为D,对称轴为 , 点A的横坐标分别为 , 与y轴交于点C.下面五个结论:①;②;③;④;⑤ , 是抛物线上两点 , 若 , 则 . 其中正确的结论有( )
A、 B、 C、 D、12. 如图,抛物线的顶点为D,对称轴为 , 点A的横坐标分别为 , 与y轴交于点C.下面五个结论:①;②;③;④;⑤ , 是抛物线上两点 , 若 , 则 . 其中正确的结论有( ) A、①②③ B、②③④ C、①③⑤ D、②④⑤
A、①②③ B、②③④ C、①③⑤ D、②④⑤二、填空题
-
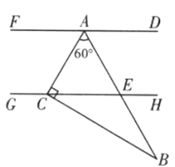
13. -x的相反数是 .14. 要使有意义,则x的取值范围是 .15. 如图,一块直角三角板的 角的顶点A与直角顶点C分别在两平行线 上,斜边 平分 ,交直线 于点E , 则 的度数为 .
 16. 因式分解:.17. 如图,边长为8的正方形中,点E在上,且 , 连接并延长至点F,连接 , 若 , 则的长度是 .
16. 因式分解:.17. 如图,边长为8的正方形中,点E在上,且 , 连接并延长至点F,连接 , 若 , 则的长度是 .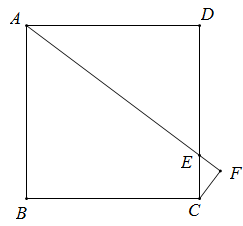 18. a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是 , 的“哈利数”是 , 已知, , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则 .
18. a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是 , 的“哈利数”是 , 已知, , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则 .三、解答题
-
19. 2021年10月11日,《生物多样性公约》缔约方大会第十五次会议()第一阶段会议在云南昆明顺利召开,某学校组织了“生物多样性知识竞赛”,将最终成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,小李随机调查了部分参赛同学的竞赛成绩,绘制了如下统计图.
抽样调查竞赛成绩人数统计表
成绩
人数
A.优秀
36人
B.良好
m人
C.合格
25人
D.不合格
n人
 (1)、本次抽样调查的样本容量是 , 统计表中 , .(2)、扇形统计图中,表示等级A的扇形圆心角为度.(3)、该校共有3000名学生,试估计该校竞赛成绩达“良好”以上(包括“良好”)的学生大约有多少名?20. 数学课上,老师给大家出了这样一道题:当时,计算的值,粗心的小明同学把“”错抄成“”,但他的计算结果也正确,请你通过计算说明这是怎么回事?21. 随着第24届北京冬奥会和冬残奥会的顺利召开,“冰墩墩”和“雪容融”成为了大家竞相追捧的吉祥物,某商家迅速抓住这一商机,购进了一批“冰墩墩”和“雪容融”小挂件,已知2个“冰墩墩”和1个“雪容融”小挂件共需26元,4个“冰墩墩”和3个“雪容融”小挂件共需62元.(1)、“冰墩墩”和“雪容融”小挂件单价各是多少元?(2)、如果这一商家准备再购进相同的“冰墩墩”和“雪容融”小挂件共100个,且“雪容融”的数量不少于“冰墩墩”数量的 , 请设计出最省钱的购买方案,并求出最少费用.22. 如图,矩形中,对角线 , 相交于点O,过点O作 , 交于点E,交于点F.
(1)、本次抽样调查的样本容量是 , 统计表中 , .(2)、扇形统计图中,表示等级A的扇形圆心角为度.(3)、该校共有3000名学生,试估计该校竞赛成绩达“良好”以上(包括“良好”)的学生大约有多少名?20. 数学课上,老师给大家出了这样一道题:当时,计算的值,粗心的小明同学把“”错抄成“”,但他的计算结果也正确,请你通过计算说明这是怎么回事?21. 随着第24届北京冬奥会和冬残奥会的顺利召开,“冰墩墩”和“雪容融”成为了大家竞相追捧的吉祥物,某商家迅速抓住这一商机,购进了一批“冰墩墩”和“雪容融”小挂件,已知2个“冰墩墩”和1个“雪容融”小挂件共需26元,4个“冰墩墩”和3个“雪容融”小挂件共需62元.(1)、“冰墩墩”和“雪容融”小挂件单价各是多少元?(2)、如果这一商家准备再购进相同的“冰墩墩”和“雪容融”小挂件共100个,且“雪容融”的数量不少于“冰墩墩”数量的 , 请设计出最省钱的购买方案,并求出最少费用.22. 如图,矩形中,对角线 , 相交于点O,过点O作 , 交于点E,交于点F.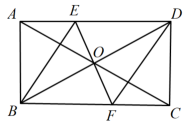 (1)、求证:四边形为菱形;(2)、若 , , 求线段的长度.
(1)、求证:四边形为菱形;(2)、若 , , 求线段的长度.
