云南省昆明市安宁市2022年初中学业水平考试第一次模拟测试数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数 $0 ， π ， | - 2 | ， - 1$ 中，最小的数是（）

A、 $| - 2 |$ B、0 C、-1 D、 $π$

查看试题解析
2. 下列运算正确的是（）

A、 $3 \sqrt{2} - \sqrt{2} = 2$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(- 3)}^{- 2} = \frac{1}{9}$ D、 ${(- 3 a^{3} b)}^{2} = 6 a^{6} b^{2}$

查看试题解析
3. 如图，已知 $A B$ 、 $C D$ 是 $⊙ O$ 的两条直径， $∠ A B C = 28 °$ ，那么 $∠ B A D =$ （）

A、62° B、56° C、42° D、28°

查看试题解析
4. 要使分式 $\frac{x - 3}{x}$ 有意义，则 $x$ 的取值范围为（）

A、 $x \geq 3$ B、 $x \neq 3$ C、 $x > 0$ D、 $x \neq 0$

查看试题解析
5. 新定义运算： $m * n = m n^{2} - 2 n - 1$ ，则方程 $- 1 * x = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
6. 下列说法不正确的是（）

A、在“双减”政策下，某校为了解八年级500名学生的睡眠时间，随机选择了该年级200名学生进行调查，则样本容量是200 B、“画一个正六边形，它的外角和是360°”属于必然事件 C、调查江苏卫视大型科学竞技真人秀《最强大脑》节目的收视率，应采用全面调查 D、在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数可能是5个

查看试题解析
7. 观察下列等式： $1 = 1^{2}$ ， $1 + 3 = 2^{2}$ ， $1 + 3 + 5 = 3^{2}$ ， $1 + 3 + 5 + 7 = 4^{2}$ ， …，则 $1 + 3 + 5 + 7 + 9 + ⋯ 2021 =$ （）

A、 $101 0^{2}$ B、 $101 1^{2}$ C、 $101 2^{2}$ D、 $202 1^{2}$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，按以下步骤作图：①以 $B$ 为圆心，任意长为半径作弧，分别交 $B A$ 、 $B C$ 于 $M$ 、 $N$ 两点；②分别以 $M$ 、 $N$ 为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点 $P$ ；③作射线 $B P$ ，交边 $A C$ 于 $D$ 点．若 $A B = 10$ ， $B C = 6$ ，则线段 $C D$ 的长为（）

A、3 B、 $\frac{10}{2}$ C、 $\frac{8}{3}$ D、 $\frac{16}{5}$

查看试题解析
9. 关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - 2 > 4 (x - 1) \\ x - 2 a < 0 \end{array}$ 的解集为 $x < 2$ ，那么 $a$ 的取值范围是（）

A、 $a = 1$ B、 $a > 1$ C、 $a < 1$ D、 $a \geq 1$

查看试题解析
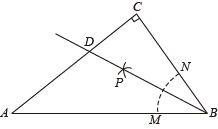10. 在锐角△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论： $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2 R$ （其中R为△ABC的外接圆半径）成立.在△ABC中，若∠A=75°，∠B=45°，c=4，则△ABC的外接圆面积为（）

A、 $\frac{16 π}{3}$ B、 $\frac{64 π}{3}$ C、 $16 π$ D、 $64 π$

查看试题解析

二、填空题

11. $\frac{9}{25}$ 的平方根是．

查看试题解析
12. 化简： $\frac{x^{2}}{x - 2} + \frac{4}{2 - x}$ = ．

查看试题解析
13. 正比例函数 $y = k_{1} x$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于A ， B两点，若A点坐标为 $(\sqrt{3} ， - 2 \sqrt{3})$ ，则 $k_{1} + k_{2} =$ ．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C = 4 c m$ ， $∠ A = 60 °$ ， $∠ B = 45 °$ ， $B C$ 边的垂直平分线 $D E$ 交 $A B$ 于点 $D$ ，连接 $C D$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

四、八年级抽取学生的测试成绩统计表

五、

15. 某校七、八年级各有500名学生，为了解该校七、八年级学生对党史知识的掌握情况，从七、八年级学生中各随机抽取15人进行党史知识测试，统计这部分学生的测试成绩（成绩均为整数，满分10分，8分及以上为优秀），相关数据统计、整理如下：七年级抽取学生的成绩：6，6，6，8，8，8，8，8，8，8，9，9，9，9，10；
七、八年级抽取学生的测试成绩统计表

年级七年级八年级

平均数 8 8

众数 a 7

中位数 8 b

优秀率 80% 60%

(1)、填空： $a =$ ， $b =$ ；

(2)、根据以上数据，你认为该校七、八年级中，哪个年级的学生党史知识掌握得较好？请说明理由（写出一条即可）；

(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数；

查看试题解析
16. 为了加快推进我国全民新冠病毒疫苗接种，在全国范围内构筑最大免疫屏障，各级政府积极开展接种新冠病毒疫苗的宣传工作．某社区印刷了多套宣传海报，每套海报四张，海报内容分别是：
A.防疫道路千万条，接种疫苗第一条；

B ．疫苗接种保安全，战胜新冠靠全员；

C ．接种疫苗别再拖，安全保障好处多；

D ．疫苗接种连万家，平安健康乐全家．

志愿者小张和小李利用休息时间到某小区张贴海报．

(1)、小张从一套海报中随机抽取一张，抽到B海报的概率是．

(2)、小张和小李从同一套海报中各随机抽取一张，用列表法或画树状图法，求他们两个人中有一个人抽到D海报的概率．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 交 $B C$ 于点 $D$ ，过点 $D$ 作 $E F ⊥ A C$ 于点 $E$ ，交 $A B$ 的延长线于点 $F$ ，连接 $A D$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线．

(2)、求证： $△ F B D ∽ △ F D A$ ．

(3)、若 $D F = 4$ ， $B F = 2$ ，求 $⊙ O$ 的半径长．

查看试题解析
18. 某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入，试销的30天中，该村第一天卖出土特产42千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出6千克，第x天的售价为y元/千克，y关于x的函数解析式为y＝ ${\begin{matrix} m x - 82 m (1 \leq x < 20) \\ n (20 \leq x \leq 30) \end{matrix}$ ，x为正整数，且第14天的售价为34元/千克，第27天的售价为27元/千克.已知土特产的成本是21元/千克，每天的利润是W元（利润＝销售收入﹣成本）.

(1)、m＝， n＝；

(2)、求每天的利润W元与销售的天数x（天）之间的函数关系式；

(3)、在销售土特产的30天中，当天利润不低于1224元的共有多少天？

查看试题解析
19. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A$ 、 $B$ （ $A$ 与 $B$ 的左侧），交 $y$ 轴的负半轴于点 $C$ ， $O C = 3 O B$ ， $B$ 点的坐标为 $(1 ， 0)$ ．

(1)、求抛物线的解析式；

(2)、点 $D$ 是抛物线对称轴与 $x$ 轴的交点，点 $P$ 是第三象限内抛物线上一点，当 $△ P C D$ 面积最大时，求点 $P$ 的坐标；

(3)、在（2）的结论下，绕点 $D$ 旋转直线 $C D$ 得到直线 $l$ ，当直线 $l$ 经过点 $P$ 时停止旋转，在旋转过程中，直线 $l$ 与线段 $C P$ 交于点 $N$ ，设点 $C$ ， $P$ 到直线 $l$ 的距离分别为 $d_{1}$ ， $d_{2}$ ，当 $d_{1} + d_{2}$ 最大时，求直线 $l$ 旋转的角度．

查看试题解析

年级	七年级	八年级
平均数	8	8
众数	a	7
中位数	8	b
优秀率	80%	60%