天津市和平区2022年中考一模数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 的值是( )A、 B、 C、 D、2. 下列图形是中心对称图形而不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、04. 如图是由5个大小相同的小正方体搭成的几何体,它的左视图是( )
3. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、04. 如图是由5个大小相同的小正方体搭成的几何体,它的左视图是( )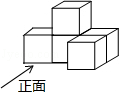 A、
A、 B、
B、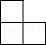 C、
C、 D、
D、 5. 如图是一个正五棱柱,它的俯视图是( )
5. 如图是一个正五棱柱,它的俯视图是( )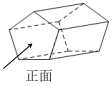 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,将△ABC绕点A逆时针旋转70°得到△ADE,点B、C的对应点分别为D、E,当点B、C、D、P在同一条直线上时,则∠PDE的度数为( )
6. 如图,将△ABC绕点A逆时针旋转70°得到△ADE,点B、C的对应点分别为D、E,当点B、C、D、P在同一条直线上时,则∠PDE的度数为( )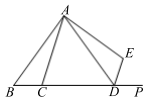 A、55° B、70° C、80° D、110°7. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ).
A、55° B、70° C、80° D、110°7. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ). A、 B、 C、 D、8. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,设每个支干长出x个小分支,则下列方程正确的是( )A、1+x2=91 B、(1+x)2=91 C、1+x+x2=91 D、1+(1+x)+(1+x)2=919. 反比例函数y=(是常数,)的图象如图所示,则下列说法:①m>0;②若P(x,y)在图象上,则P'(﹣x,﹣y)也一定在图象上;在每个象限内,y随x的增大而增大;③若A(﹣1,h),B(2,k)在图象上,则h<k;④若点A , B都在该函数的图象上,且 , 则 . 其中,正确结论的个数是( )
A、 B、 C、 D、8. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,设每个支干长出x个小分支,则下列方程正确的是( )A、1+x2=91 B、(1+x)2=91 C、1+x+x2=91 D、1+(1+x)+(1+x)2=919. 反比例函数y=(是常数,)的图象如图所示,则下列说法:①m>0;②若P(x,y)在图象上,则P'(﹣x,﹣y)也一定在图象上;在每个象限内,y随x的增大而增大;③若A(﹣1,h),B(2,k)在图象上,则h<k;④若点A , B都在该函数的图象上,且 , 则 . 其中,正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.则正方形ABCD与正六边形AEFCGH的周长之比为( )
A、1个 B、2个 C、3个 D、4个10. 如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.则正方形ABCD与正六边形AEFCGH的周长之比为( ) A、 ∶ 3 B、 ∶1 C、 ∶ D、1∶11. 如图,已知第一象限内的点A在反比例函数y=上,第二象限的点B在反比例函数(是常数,)上,且OA⊥OB, , 则k的值为( )
A、 ∶ 3 B、 ∶1 C、 ∶ D、1∶11. 如图,已知第一象限内的点A在反比例函数y=上,第二象限的点B在反比例函数(是常数,)上,且OA⊥OB, , 则k的值为( ) A、8 B、﹣4 C、﹣6 D、﹣812. 已知二次函数y=(m﹣2)x2+2mx+m﹣3(是常数)的图象与x轴有两个交点(x1 , 0),(x2 , 0), , 则下列说法:①该二次函数的图象一定过定点(﹣1,﹣5);②若该函数图象开口向下,则m的取值范围为:;③若m=3,当≤x≤0时,y的最大值为0,最小值为﹣9,则t的取值范围为 . 其中,正确的个数为( )A、0个 B、1个 C、2个 D、3个
A、8 B、﹣4 C、﹣6 D、﹣812. 已知二次函数y=(m﹣2)x2+2mx+m﹣3(是常数)的图象与x轴有两个交点(x1 , 0),(x2 , 0), , 则下列说法:①该二次函数的图象一定过定点(﹣1,﹣5);②若该函数图象开口向下,则m的取值范围为:;③若m=3,当≤x≤0时,y的最大值为0,最小值为﹣9,则t的取值范围为 . 其中,正确的个数为( )A、0个 B、1个 C、2个 D、3个二、填空题
-
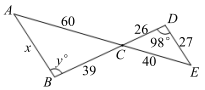
13. 已知y是x的反比例函数,当x=3时,y=﹣4,则当x=﹣2时,y= .14. 如图,则x= , y= .
 15. 一个不透明的口袋中有三个完全相同的小球,其中2个小球印有冰墩墩图案,1个小球印有雪容融图案,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球恰好一个是冰墩墩,一个是雪容融的概率为 .16. 若一次函数y=2x+b(b是常数)向上平移5个单位后,图象经过第一、二、三象限,则b的取值范围是 .17. 如图,已知A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°,⊙O的半径为1,则四边形APBC的面积最大值为 .
15. 一个不透明的口袋中有三个完全相同的小球,其中2个小球印有冰墩墩图案,1个小球印有雪容融图案,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球恰好一个是冰墩墩,一个是雪容融的概率为 .16. 若一次函数y=2x+b(b是常数)向上平移5个单位后,图象经过第一、二、三象限,则b的取值范围是 .17. 如图,已知A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°,⊙O的半径为1,则四边形APBC的面积最大值为 .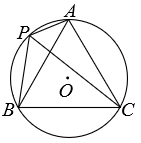
三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A落在格点上,点B,点C均在网格线上,△ABC的外接圆交网格线于点D,△ABC的外接圆的圆心为O.
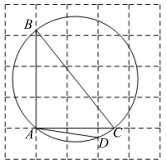
(Ⅰ)BC为⊙O的 ▲ ;
(Ⅱ)⊙O上有一点P,连接DP,满足DP=AD,请在如图所示的网格中,用无刻度的直尺画出点P,并简要说明点P的位置是如何找到的(不要求证明) ▲ .
19. 关于x的一元二次方程x2﹣4x+k﹣1=0.(1)、若k=1,求方程的根;(2)、若方程有两个不相等的实数根,求k的取值范围.20. 已知二次函数y=ax2+bx+c(a、b、c是常数,a≠0)的自变量x和函数值y部分对应值如下表:x
…
0
1
2
3
4
…
y
…
3
0
-1
0
m
…
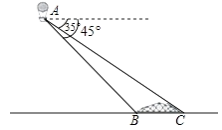
(1)、抛物线的对称轴为;(2)、m的值为;(3)、求该抛物线的解析式;(4)、若点A(),B()都在函数图象上,且 , 则(填“>”,“<”或“=”).21. 已知四边形ABCD内接于⊙O,AB为⊙O的直径,E是AB延长线上一点,连接AC,CE.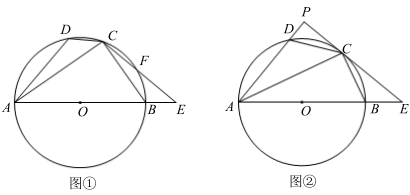 (1)、如图①,若CE交⊙O于点F, , ∠D=125°,∠DAC=15°,求∠E和∠CAB的大小;(2)、如图②,若CE与⊙O相切于点C,延长AD交EC于点P, , AB=10,DP+PC=6,求∠P的大小和AD的长度.22. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)
(1)、如图①,若CE交⊙O于点F, , ∠D=125°,∠DAC=15°,求∠E和∠CAB的大小;(2)、如图②,若CE与⊙O相切于点C,延长AD交EC于点P, , AB=10,DP+PC=6,求∠P的大小和AD的长度.22. 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)【参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70】
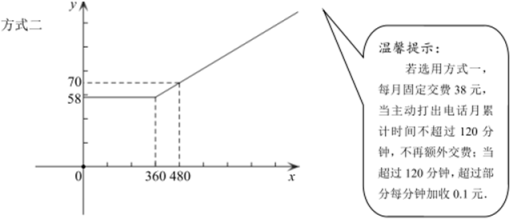
 23. 某通讯公司推出了移动电话的两种计费方式,设一个月内使用移动电话主叫的时间为分钟 , 方式一,方式二的月使用费用分别为元,元,两种计费方式被叫均免费.其中方式一月使用费详情见下表,方式二的月使用费元与主叫时间分钟的函数图象如图所示.
23. 某通讯公司推出了移动电话的两种计费方式,设一个月内使用移动电话主叫的时间为分钟 , 方式一,方式二的月使用费用分别为元,元,两种计费方式被叫均免费.其中方式一月使用费详情见下表,方式二的月使用费元与主叫时间分钟的函数图象如图所示.月使用费/元
主叫限定时间/分钟
主叫超时费/(元/分钟)
被叫
方式一
38
120
0.1
免费
 (1)、根据题意填表:
(1)、根据题意填表:表格一:
主叫时间x分钟
x=100
x=320
x>120
方式一计费/元
y1=
表格二:
月使用费/元
主叫限定时间/分钟
主叫超时费/(元/分钟)
被叫
方式二
免费
(2)、结合图象信息,求与的函数解析式,并写出自变量的取值范围;(3)、选用哪种计费方式花费少(直接写出结果即可).24. 在平面直角坐标系中,△AOB为直角三角形,点O(0,0),点A(0,3),点B在轴的正半轴上,∠OAB=30°,点P为AB的中点.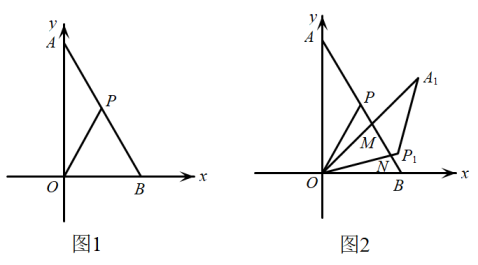 (1)、如图①,求点P的坐标;(2)、以点O为中心,顺时针旋转△AOP,得到△A1OP1 , 记旋转角为(),点A,P的对应点分别为A1 , P1 .
(1)、如图①,求点P的坐标;(2)、以点O为中心,顺时针旋转△AOP,得到△A1OP1 , 记旋转角为(),点A,P的对应点分别为A1 , P1 .①如图②,线段OA1交线段AB于点M,线段OP1交线段AB于点N,当△OMN为等腰三角形时,求点A1的坐标;
②直线OA1交直线AB于点M,直线OP1交线段AB于点N,当△OMN为等腰三角形时,求的度数(直接写出结果即可).
25. 已知抛物线(是常数,)的图象经过点A , B , 与轴交于点C,点P .(1)、求抛物线解析式和点C的坐标;(2)、过点D(0,)作直线⊥轴,将抛物线向上平移,顶点E落在直线上,若点P为抛物线一点,平移后对应点为P',当DP=DP'时,求点P的坐标;(3)、若点P为抛物线对称轴上一动点,连接PA、PC,若∠APC不小于60°,求的取值范围.