山西省临汾市2022年中考考前适应性训练(二模)数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )A、55×106 B、5.5×107 C、5.5×108 D、0.55×1084. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( )
3. 2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )A、55×106 B、5.5×107 C、5.5×108 D、0.55×1084. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( ) A、 B、 C、 D、5. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)6. 不等式组的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)6. 不等式组的解集在数轴上表示正确的是( )A、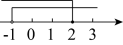 B、
B、 C、
C、 D、
D、 7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、8. 某工厂生产 、 两种型号的扫地机器人. 型机器人比 型机器人每小时的清扫面积多50%;清扫 所用的时间 型机器人比 型机器人多用40分钟. 两种型号扫地机器人每小时分别清扫多少面积?若设 型扫地机器人每小时清扫 ,根据题意可列方程为( )A、 B、 C、 D、9. 在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).
A、 B、 C、 D、8. 某工厂生产 、 两种型号的扫地机器人. 型机器人比 型机器人每小时的清扫面积多50%;清扫 所用的时间 型机器人比 型机器人多用40分钟. 两种型号扫地机器人每小时分别清扫多少面积?若设 型扫地机器人每小时清扫 ,根据题意可列方程为( )A、 B、 C、 D、9. 在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).类型
健康
亚健康
不健康
数据(人)
32
7
1
A、32 B、7 C、 D、10. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为( )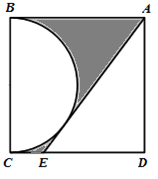 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
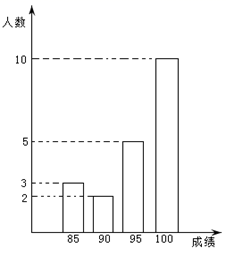
11. 计算 的结果是 .12. 观察下列各项: , , , ,…,则第 项是.13. 某学校八年级(2)班有20名学生参加学校举行的“学党史、看红书”知识竞赛,成绩统计如图.这个班参赛学生的平均成绩是 .
 14. 如图,点O是半圆圆心, 是半圆的直径,点A , D在半圆上,且 ,过点D作 于点C , 则阴影部分的面积是 .
14. 如图,点O是半圆圆心, 是半圆的直径,点A , D在半圆上,且 ,过点D作 于点C , 则阴影部分的面积是 .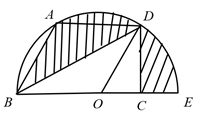 15. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移长度a(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的长为 .
15. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移长度a(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的长为 .
三、解答题
-
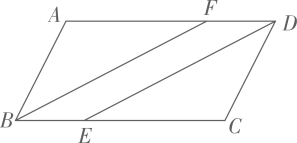
16.(1)、计算: .(2)、已知 , 求的值.17. 如图,点E,F在 的边 , 上, , ,连接 , .求证:四边形 是平行四边形.
 18. 为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.(1)、这两种消毒液的单价各是多少元?(2)、学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不少于A型消毒液数量的 ,请设计出最省钱的购买方案,并求出最少费用.19. 小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如下测试成绩折线统计图.根据图中信息,解答下列问题:
18. 为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.(1)、这两种消毒液的单价各是多少元?(2)、学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不少于A型消毒液数量的 ,请设计出最省钱的购买方案,并求出最少费用.19. 小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如下测试成绩折线统计图.根据图中信息,解答下列问题: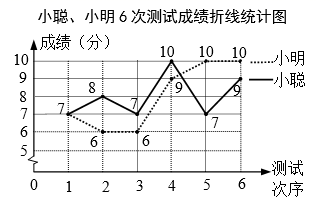 (1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.20. 如图1是某中学教学楼的推拉门,已知门的宽度米,且两扇门的大小相同(即),将左边的门 , 绕门轴向里面旋转 , 将右边的门绕门轴向外面旋转 , 其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据)
(1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.20. 如图1是某中学教学楼的推拉门,已知门的宽度米,且两扇门的大小相同(即),将左边的门 , 绕门轴向里面旋转 , 将右边的门绕门轴向外面旋转 , 其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据) 21. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
21. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.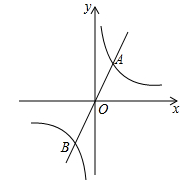 (1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.22. 在等腰 中, ,点D是 边上一点(不与点B、C重合),连结 .
(1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.22. 在等腰 中, ,点D是 边上一点(不与点B、C重合),连结 . (1)、如图1,若 ,点D关于直线 的对称点为点E,结 , ,则 ;(2)、若 ,将线段 绕点A顺时针旋转 得到线段 ,连结 .
(1)、如图1,若 ,点D关于直线 的对称点为点E,结 , ,则 ;(2)、若 ,将线段 绕点A顺时针旋转 得到线段 ,连结 .①在图2中补全图形;
②探究 与 的数量关系,并证明;
(3)、如图3,若 ,且 ,试探究 、 、 之间满足的数量关系,并证明.23. 在平面直角坐标系中,已知抛物线经过 , , 三点. (1)、求抛物线的解析式;(2)、若点为第三象限内抛物线上一动点,点的横坐标为 , 的面积为 , 求关于的函数关系式,并求出的最大值.(3)、若点是抛物线上的动点,点是直线 上的动点,若以点、、、为顶点的四边形为平行四边形,直接写出相应的点的坐标.
(1)、求抛物线的解析式;(2)、若点为第三象限内抛物线上一动点,点的横坐标为 , 的面积为 , 求关于的函数关系式,并求出的最大值.(3)、若点是抛物线上的动点,点是直线 上的动点,若以点、、、为顶点的四边形为平行四边形,直接写出相应的点的坐标.