山东省烟台市2022年中考模拟数学试题(二)
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 的平方根为( )A、13 B、±13 C、 D、±2. 下列计算正确的是( )A、 B、 C、 D、3. 在下列命题中,为真命题的是( )A、相等的角是对顶角 B、平行于同一条直线的两条直线互相平行 C、同旁内角互补 D、垂直于同一条直线的两条直线互相垂直4. 某玩具商店周年店庆,全场八折促销,持会员卡可在促销活动的基础上再打六折.某电动汽车原价300元,小明持会员卡购买这个电动汽车需要花( )元A、240 B、180 C、160 D、1445. 已知 ,运用科学计算器求锐角 时(在开机状态下),按下的第一个键是( )A、
 B、
B、 C、
C、 D、
D、 6. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、7. 已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );A、180° B、200° C、216° D、225°8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )
6. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、7. 已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );A、180° B、200° C、216° D、225°8. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )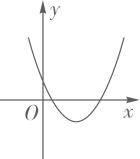 A、
A、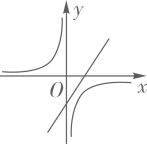 B、
B、 C、
C、 D、
D、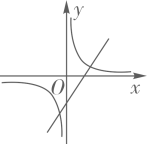 9. 如图,已知 , ,以O为位似中心,把 缩小到原来的 ,则点E的对应点的坐标为是( )
9. 如图,已知 , ,以O为位似中心,把 缩小到原来的 ,则点E的对应点的坐标为是( )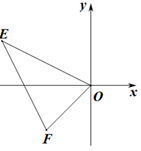 A、 B、 或 C、 或 D、10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )
A、 B、 或 C、 或 D、10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )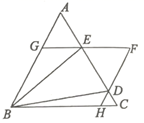 A、①②③ B、①②④ C、①②③④ D、②③④
A、①②③ B、①②④ C、①②③④ D、②③④二、填空题
-
11. 2021年5月19日,第三届阿里数学竞赛预选赛顺利结束,本届大赛在全球范围内吸引了约5万名数学爱好者参加,阿里数学竞赛旨在全球范围内引领开启关注数学、理解数学、欣赏数学、助力数学的科学风尚.5万用科学记数法表示为 .12. 边长为a , b的长方形的周长为14,面积为10,则 的值为 .
 13. 已知一组数据:92,94,98,91,95的中位数为a,方差为b,则 .14. 不等式组 的解集为 .15. 定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“倍角三角形”,其中α称为“倍角”,如果一个“倍角三角形”的一个内角为99°,那么倍角α的度数是 .16. 某工程需要在规定日期内完成,如果甲工程队单独做,恰好如期成:如果乙工程队单独做,则超过规定日期3天,现在甲、乙两队合做2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期.如果设规定日期为x天,根据题意列方程得 .17. 如图,四边形是边长为9的正方形纸片,将其沿折叠,使点B落在边上的处,点A对应点为 , 且 , 则的长是 .
13. 已知一组数据:92,94,98,91,95的中位数为a,方差为b,则 .14. 不等式组 的解集为 .15. 定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“倍角三角形”,其中α称为“倍角”,如果一个“倍角三角形”的一个内角为99°,那么倍角α的度数是 .16. 某工程需要在规定日期内完成,如果甲工程队单独做,恰好如期成:如果乙工程队单独做,则超过规定日期3天,现在甲、乙两队合做2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期.如果设规定日期为x天,根据题意列方程得 .17. 如图,四边形是边长为9的正方形纸片,将其沿折叠,使点B落在边上的处,点A对应点为 , 且 , 则的长是 . 18. 如图,已知直线 , 过点作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点;过点作y轴的垂线交直线l于点 , 过点作直线l的垂线交y轴于点;…按此作法继续下去,则点的坐标为 .
18. 如图,已知直线 , 过点作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点;过点作y轴的垂线交直线l于点 , 过点作直线l的垂线交y轴于点;…按此作法继续下去,则点的坐标为 .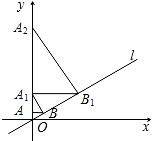
三、解答题
-
19.(1)、计算:(2)、化简求值:的值,其中 .20. 某汽车销售公司一位销售经理1—5月份的汽车销售统计图如下:
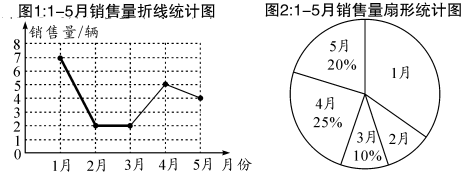 (1)、已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为辆,在扇形图中,2月的销售量所对应的扇形的圆心角大小为;(2)、补全图中销售量折线统计图;(3)、已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用G1 , G2 , G3表示,合资车分别用H1 , H2表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车”的概率.21. 为助力我省脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店七月份销售256袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到400袋.(1)、求八、九这两个月销售量的月平均增长率;(2)、若农产品每袋成本价25元,原售价为每袋40元,该网店十月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在十月份可获利4250元?22. 已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)、已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为辆,在扇形图中,2月的销售量所对应的扇形的圆心角大小为;(2)、补全图中销售量折线统计图;(3)、已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用G1 , G2 , G3表示,合资车分别用H1 , H2表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车”的概率.21. 为助力我省脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店七月份销售256袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到400袋.(1)、求八、九这两个月销售量的月平均增长率;(2)、若农产品每袋成本价25元,原售价为每袋40元,该网店十月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在十月份可获利4250元?22. 已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF. (1)、求证:四边形EGFH是平行四边形.(2)、连结BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.23. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量(件)与销售单价(元)之间的函数关系如图所示,设每月获得的利润为(元).
(1)、求证:四边形EGFH是平行四边形.(2)、连结BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.23. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量(件)与销售单价(元)之间的函数关系如图所示,设每月获得的利润为(元).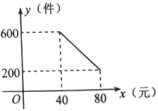 (1)、求出每月的销售量(件)与销售单价(元)之间的函数关系式;(2)、这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)、为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?24. 问题提出:在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是和 , , 现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.如何铺设使得管道长度较短?
(1)、求出每月的销售量(件)与销售单价(元)之间的函数关系式;(2)、这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)、为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?24. 问题提出:在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是和 , , 现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.如何铺设使得管道长度较短?方案设计:某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为 , 且(其中于点P);图2是方案二的示意咨图,设该方案中管道长度为 , 且(其中点与点A关于l对称,与l交于点P).
 (1)、在方案一中,(用含a的式子表示);(2)、在方案二中,组长小宇为了计算的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,(用含a的式子表示).(3)、①当时,比较大小:(填“>”、“=”或“<”);
(1)、在方案一中,(用含a的式子表示);(2)、在方案二中,组长小宇为了计算的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,(用含a的式子表示).(3)、①当时,比较大小:(填“>”、“=”或“<”);②当时,比较大小:(填“>”、“=”或“<”);
(4)、请你参考方框中的方法指导,就a(当时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案还是方案二?方法指导
当不易直接比较两个正数m与n的大小时,可以对它们的平方进行比较:
∵ , ,
∴与的符号相同.
当时, , 即;
当时, , 即m=n;
当时, , 即m<n;
25.(1)、方法呈现: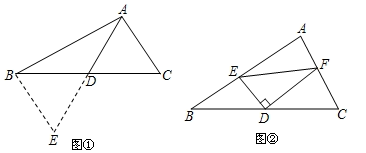
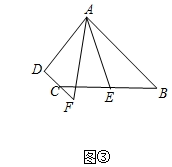
如图①:在中,若 , , 点D为BC边的中点,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 , 再连接BE,可证 , 从而把AB、AC,集中在中,利用三角形三边的关系即可判断中线AD的取值范围是 , 这种解决问题的方法我们称为倍长中线法;
(2)、探究应用:如图②,在中,点D是BC的中点,于点D,DE交AB于点E,DF交AC于点F,连接EF,判断与EF的大小关系并证明;
(3)、问题拓展:如图③,在四边形ABCD中, , AF与DC的延长线交于点F、点E是BC的中点,若AE是的角平分线.试探究线段AB,AF,CF之间的数量关系,并加以证明.