山东省临沂市蒙阴县2022年中考数学模拟试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2021的绝对值是（）

A、2021 B、 $\frac{1}{2021}$ C、 $- \frac{2}{2021}$ D、﹣2021

查看试题解析
2. 已知：点 $A (m - 1 ， 3)$ 与点 $B (2 ， n - 1)$ 关于 $x$ 轴对称，则 ${(m + n)}^{2021}$ 的值为（）

A、0 B、1 C、-1 D、 $3^{2021}$

查看试题解析
3. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是（）

A、30° B、40° C、50° D、60°

查看试题解析
4. 用配方法解方程 $x^{2} + 6 x + 4 = 0$ 时，原方程变形为（）

A、 ${(x + 3)}^{2} = 9$ B、 ${(x + 3)}^{2} = 13$ C、 ${(x + 3)}^{2} = 5$ D、 ${(x + 3)}^{2} = 4$

查看试题解析
5. 如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将∠C沿DE对折，使点C落在△ABC外的点C′处，若∠1＝20°，则∠2的度数为（）

A、80° B、90° C、100° D、110°

查看试题解析
6. 如图，在△ABC中， $\frac{A D}{A C} = \frac{A E}{A B}$ ，则下列等式不成立的是（）

A、 $∠ A D E = ∠ A C B$ B、 $∠ A E D = ∠ A B C$ C、 $\frac{△ A D E 的周长}{△ A C B 的周长} = \frac{A D}{A C}$ D、 $\frac{A E}{A C} = \frac{D E}{B C}$

查看试题解析
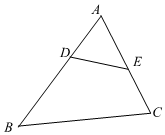7. 如图是一圆锥的左视图，根据图中所示数据，可得圆锥侧面展开图的圆心角的度数为（）

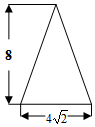A、60° B、90° C、120° D、135°

查看试题解析
8. 如图，小球从A口往下落，在每个交叉口都有向左或向右两种可能，且可能性相同，则小球最终从E口落出的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

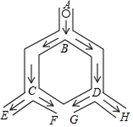查看试题解析
9. 测试五位学生的“立定跳远”成绩，得到5个互不相同的数据，在统计时出现一处不符合题意，将最低成绩写得更低了，计算不受影响的是（）

A、方差 B、标准差 C、平均数 D、中位数

查看试题解析
10. 八年级学生去距学校s千米的博物馆参观，一部分同学骑自行车先走，过了1小时后，其余同学乘汽车出发，结果他们同时到达.已知汽车的速度是骑车同学速度的m倍，设骑车同学的速度为x千米/小时，则可列方程（）

A、 $\frac{s}{x}$ = $\frac{s}{m x}$ +1 B、 $\frac{s}{m x}$ - $\frac{s}{x}$ =1 C、 $\frac{1}{x}$ = $\frac{1}{m x}$ +1 D、 $\frac{s}{m x - x}$ =1

查看试题解析
11. 如图1，在Rt△ABC中，∠B＝90°，∠ACB＝45°，延长BC到D，使CD＝AC，则tan22.5°＝（）

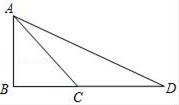A、 $\sqrt{2} + 1$ B、 $\sqrt{2} - 1$ C、 $\frac{\sqrt{2} + 1}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
12. 如图，第1个图形中小黑点的个数为5个，第2个图形中小黑点的个数为9个，第3个图形中小黑点的个数为13个，…，按照这样的规律，第n个图形中小黑点的个数应该是（）

A、 $4 n + 1$ B、 $3 n + 2$ C、 $5 n - 1$ D、 $6 n - 2$

查看试题解析
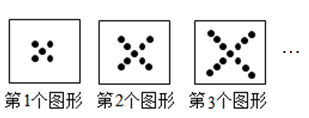13. 如图，在 $▱ A B C D$ 中，添加下列条件仍不能判定 $▱ A B C D$ 是菱形的是（）

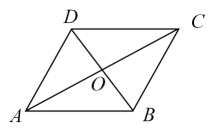A、AC $⊥$ BD B、AB=BC C、AC=BD D、 $∠ D A C = ∠ B A C$

查看试题解析
14. 直线y=﹣2x﹣1关于y轴对称的直线与直线y=﹣2x+m的交点在第四象限，则m的取值范围是（）

A、m>﹣1 B、m<1 C、﹣1<m<1 D、﹣1≤m≤1

查看试题解析

二、填空题

15. 在实数范围内因式分解：2x²+3x﹣4＝．

查看试题解析
16. 如图，四边形ABCD，∠B＝∠C＝90°，边BC上一点E，连结AE、DE得等边△ADE，若 $\frac{A B}{C D}$ ＝ $\frac{2}{3}$ ，则 $\frac{C E}{B E}$ ＝

查看试题解析
17. 计算： $(\frac{m}{m - 2} - \frac{m}{m + 2}) \cdot \frac{2 - m}{m}$ ＝．

查看试题解析
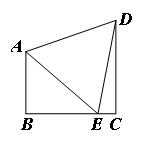18. 设α是锐角，如果tanα＝3，那么cotα＝．

查看试题解析
19. 读一读：式子“ $1 + 2 + 3 + 4 + \dots + 100$ ”表示从1开始的100个连续自然数的和，由于式子比较长，书写不方便，为了简便起见，我们将其表示为 $\sum_{n = 1}^{100} n$ ，这里“ $\sum$ ”是求和符号，通过对以上材料的阅读，计算 $\sum_{n = 1}^{2016} \frac{1}{n (n + 1)} =$ ．

查看试题解析

三、解答题

20. 计算： $2^{- 1} + \sqrt{16} - {(3 - \sqrt{3})}^{0} + | \sqrt{2} - \frac{1}{2} |$

查看试题解析
21. 《如果想毁掉一个孩子，就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上，法国教育部宣布从2018年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人.

请你根据以上信息解答下列问题：

(1)、在扇形统计图中，“玩游戏”对应的百分比为，圆心角度数是度；

(2)、补全条形统计图；

(3)、该校共有学生2100人，估计每周使用手机时间在2小时以上（不含2小时）的人数.

查看试题解析
22. 某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥．如图，河旁有一座小山，山高 $B C = 80 m$ ，点C、A与河岸E、F在同一水平线上，从山顶B处测得河岸E和对岸F的俯角分别为 $∠ D B E = 45 °$ ， $∠ D B F = 31 °$ ．若在此处建桥，求河宽 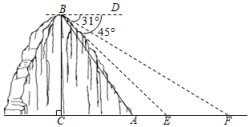$E F$ 的长．（结果精确到 $1 m$ ）[参考数据： $s i n 31 ° ≈ 0.52$ ， $c o s 31 ° ≈ 0.86$ ， $t a n 31 ° \approx 0.60$ $]$

查看试题解析
23. 如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．

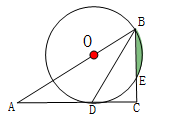(1)、求证：AC是⊙O的切线；

(2)、若OB=10，CD= $5 \sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析
24. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车必货车晚出发1.5小时，如图，线段OA表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：

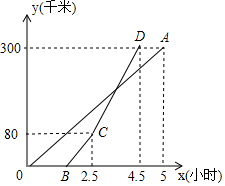(1)、轿车到乙地时，求货车与甲地的距离；

(2)、求线段CD对应的函数表达式；

(3)、在轿车行进过程，轿车行驶多少时间，两车相距15千米．

查看试题解析
25. 如图①，在矩形ABCD中，AB＝6，BC＝8，四边形EFGH是正方形，EH与BD重合，将图①中的正方形EFGH绕着点D逆时针旋转．

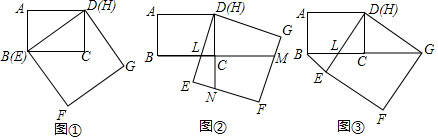(1)、旋转至如图②位置，DE交BC于点L．延长BC交FG于点M，延长DC交EF于点N．试判断DL、EN、GM之间满足的数量关系，并说明理由：

(2)、旋转至如图③位置，使点G落在BC的延长线上，DE交BC于点L，连接BE，求BE的长．

查看试题解析
26. 如图1，在平面直角坐标系中，已知A(-1，0)、C、(0，-2)，以AC为一边向右上方作正方形ACDE，其中点D在第四象限，点E在第一象限，过点E作直线 l∥y轴．抛物线y=ax²+bx+c(a≠0)的对称轴为直线 l，且经过A、C两点，与x轴的另一交点为B．

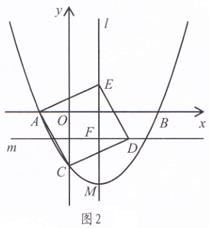(1)、点E的坐标为，该抛物的函数表达式为；

(2)、设抛物线的顶点为M，连接MB．在抛物线上是否存在点N，使∠NBA= $\frac{1}{2}$ ∠MBA?若存在，请求出所有满足条件的点N的坐标：若不存在，请说明理由．

(3)、过点D作直线m∥x轴，交直线l于点F，如图2．动点P从抛物线的顶点M出发，沿抛物线的对称轴l向上运动，与此同时，动点Q从点F出发，沿直线m向右运动，连接PQ、PB、BQ．设P、Q两点运动的速度均为1个单位长度／秒，运动的时间为t秒，△PBQ的面积为S．请直接写出S与t之间的函数关系式，并写出自变量t的取值范围.

查看试题解析