山东省聊城临清市2022年中考一模数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 实数4的平方根是( )A、 B、2 C、±2 D、2. 直六棱柱如图所示,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( )
3. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( ) A、15° B、20° C、25° D、30°4. 下列生活中的事件,属于不可能事件的是( )A、3天内将下雨 B、打开电视,正在播新闻 C、买一张电影票,座位号是偶数号 D、没有水分,种子发芽5. 下列运算正确的是( )A、 B、 C、 D、6. 班级准备推选一名同学参加学校演讲比赛,在五轮班级预选赛中,甲、乙、丙三名同学五轮预选赛成绩的平均数和方差如下表所示:
A、15° B、20° C、25° D、30°4. 下列生活中的事件,属于不可能事件的是( )A、3天内将下雨 B、打开电视,正在播新闻 C、买一张电影票,座位号是偶数号 D、没有水分,种子发芽5. 下列运算正确的是( )A、 B、 C、 D、6. 班级准备推选一名同学参加学校演讲比赛,在五轮班级预选赛中,甲、乙、丙三名同学五轮预选赛成绩的平均数和方差如下表所示:甲
乙
丙
平均数/分
96
95
97
方差
0.4
2
2
丁同学五轮预选赛的成绩依次为:97分、96分、98分、97分、97分,根据表中数据,要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛应该选择( )
A、甲 B、乙 C、丙 D、丁7. 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )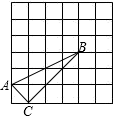 A、 B、 C、 D、8. 如图,是的外接圆, , 若的半径为1,则弦的长为( )
A、 B、 C、 D、8. 如图,是的外接圆, , 若的半径为1,则弦的长为( ) A、 B、 C、 D、9. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A、 B、 C、 D、9. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )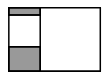 A、2 B、3 C、4 D、10. 函数的图象如图所示,则关于x的一元二次方程的根的情况是( ).
A、2 B、3 C、4 D、10. 函数的图象如图所示,则关于x的一元二次方程的根的情况是( ).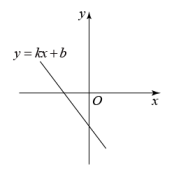 A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定11. 如图所示,将形状、大小完全相同的“”和线段按照一定规律摆成下列图形,第1幅图形中“”的个数为 , 第2幅图形中“”的个数为 , 第3幅图形中“”的个数为 , …,以此类推,则的值为( )
A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定11. 如图所示,将形状、大小完全相同的“”和线段按照一定规律摆成下列图形,第1幅图形中“”的个数为 , 第2幅图形中“”的个数为 , 第3幅图形中“”的个数为 , …,以此类推,则的值为( )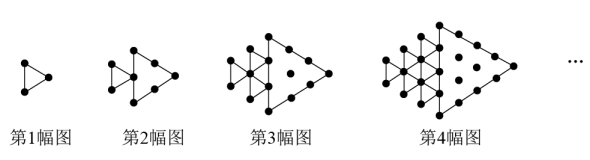 A、378 B、380 C、386 D、399
A、378 B、380 C、386 D、399二、解答题
-
12. 已知一个水分子的直径约为米,某花粉的直径约为米,用科学记数法表示一个水分子的直径是这种花粉直径的( )A、倍 B、倍 C、倍 D、倍13. 解不等式组 , 并利用数轴确定不等式组的解集.
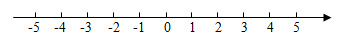 14. 如图,在中,点E,F分别在边AD和BC上,且AE=FC,连接AF,CE,分别交DC,BA的延长线于点H,G.
14. 如图,在中,点E,F分别在边AD和BC上,且AE=FC,连接AF,CE,分别交DC,BA的延长线于点H,G. (1)、求证:;(2)、当满足什么条件时,四边形是矩形?请说明理由.15. 为迎接中国共产党建党100周年,某校举行“知党史,感党恩,童心的党”系列活动,现决定组建四个活动小组,包括A(党在我心中演讲),B(党史知识竞赛),C(讲党史故事),D(大合唱).该校随机抽取了本校部分学生进行调查,以了解学生喜欢参加哪个活动小组,并将调查结果绘制成如下两幅不完整的统计图,在扇形统计图中,“B”的圆心角为 ,请结合下面两幅图中的信息解答下列问题:
(1)、求证:;(2)、当满足什么条件时,四边形是矩形?请说明理由.15. 为迎接中国共产党建党100周年,某校举行“知党史,感党恩,童心的党”系列活动,现决定组建四个活动小组,包括A(党在我心中演讲),B(党史知识竞赛),C(讲党史故事),D(大合唱).该校随机抽取了本校部分学生进行调查,以了解学生喜欢参加哪个活动小组,并将调查结果绘制成如下两幅不完整的统计图,在扇形统计图中,“B”的圆心角为 ,请结合下面两幅图中的信息解答下列问题: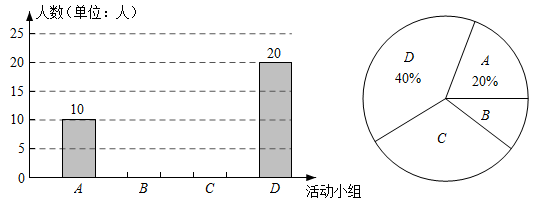 (1)、本次共调查了名学生,扇形统计图中“C”的圆心角度数为;(2)、请将条形统计图补充完整;(3)、该校共有1500名学生,根据调查数据估计该校约有多少人喜欢参加“C”活动小组.16. 为增加学生阅读量,某校购买了“科普类”和“文学类”两种书籍,购买“科普类”图书花费了3600元,购买“文学类”图书花费了2700元,其中“科普类”图书的单价比“文学类”图书的单价多20%,购买“科普类”图书的数量比“文学类”图书的数量多20本.(1)、求这两种图书的单价分别是多少元?(2)、学校决定再次购买这两种图书共100本,且总费用不超过1600元,求最多能购买“科普类”图书多少本?17. 自“新冠”病毒出现后,瓶装酒精成了人们家中常备之物.一种酒精消毒瓶如图1,为喷嘴,为按压锅,为伸缩连杆,和为导管,其示意图如图2, , , . 当按压柄按压到底时,转动到 , 此时(如图3).
(1)、本次共调查了名学生,扇形统计图中“C”的圆心角度数为;(2)、请将条形统计图补充完整;(3)、该校共有1500名学生,根据调查数据估计该校约有多少人喜欢参加“C”活动小组.16. 为增加学生阅读量,某校购买了“科普类”和“文学类”两种书籍,购买“科普类”图书花费了3600元,购买“文学类”图书花费了2700元,其中“科普类”图书的单价比“文学类”图书的单价多20%,购买“科普类”图书的数量比“文学类”图书的数量多20本.(1)、求这两种图书的单价分别是多少元?(2)、学校决定再次购买这两种图书共100本,且总费用不超过1600元,求最多能购买“科普类”图书多少本?17. 自“新冠”病毒出现后,瓶装酒精成了人们家中常备之物.一种酒精消毒瓶如图1,为喷嘴,为按压锅,为伸缩连杆,和为导管,其示意图如图2, , , . 当按压柄按压到底时,转动到 , 此时(如图3).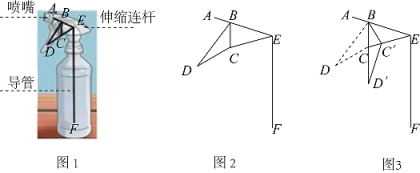 (1)、求转动到扫过的面积(结果保留);(2)、求点到直线的距离(结果精确到).
(1)、求转动到扫过的面积(结果保留);(2)、求点到直线的距离(结果精确到).(参考数据: , , , , , )
18. 如图,直线与双曲线交于点、两点,且与两坐标轴分别交于点 , .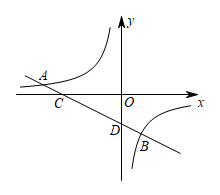 (1)、求直线的解析式;(2)、点在轴上,连接 , , 若的面积是17.5,求点的坐标.19. 如图,内接于⊙O,且为⊙O的直径,交于点 , 在的延长线上取点 , 使得∠DCE=∠B.
(1)、求直线的解析式;(2)、点在轴上,连接 , , 若的面积是17.5,求点的坐标.19. 如图,内接于⊙O,且为⊙O的直径,交于点 , 在的延长线上取点 , 使得∠DCE=∠B.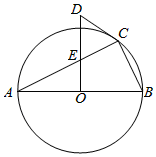 (1)、求证:是⊙O的切线;(2)、若 , , 求AE的长.20. 如图,点为坐标原点,抛物线过点 , 点是直线与抛物线的另一个交点,且点与点关于原点对称.
(1)、求证:是⊙O的切线;(2)、若 , , 求AE的长.20. 如图,点为坐标原点,抛物线过点 , 点是直线与抛物线的另一个交点,且点与点关于原点对称.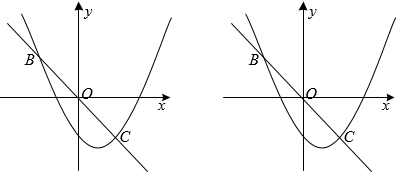 (1)、求抛物线的解析式;(2)、为抛物线上一点,它关于原点的对称点为点 .
(1)、求抛物线的解析式;(2)、为抛物线上一点,它关于原点的对称点为点 .①当四边形为菱形时,求点的坐标;
②若点的横坐标(),当为何值时,四边形面积最大,并说明理由.
三、填空题
-
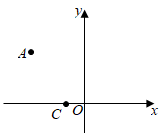
21. 若 有意义,则x的取值范围是.22. 已知 , 则 .