山东省济宁市高新区2022年中考一模数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2021 - 1$ 的相反数是（）

A、-2022 B、2022 C、 $\frac{1}{2022}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列各式是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{12}$ C、 $\sqrt{a^{2}}$ D、 $\sqrt{\frac{5}{3}}$

查看试题解析
3. 2011年3月11日日本发生9.0级大地震，福岛核电站放射性物质泄漏严重影响着海洋环境．目前全球海洋总面积约为36105.9万平方公里，用科学记数法(保留三个有效数字)表示为（）

A、3.61×10⁸平方公里 B、3.60×10⁸平方公里 C、361×10⁶平方公里 D、36100万平方公里

查看试题解析
4. 下列运算正确的是（）

A、 $a^{8} \div a^{4} = a^{2}$ B、 $(a^{2})^{2} = a^{4}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $a^{2} + a^{2} = 2 a^{4}$

查看试题解析
5. 在一次数学答题比赛中，五位同学答对题目的个数分别为7，5，3，5，10，则关于这组数据的说法不正确的是（）

A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.6

查看试题解析
6. 如图在 $4 \times 4$ 的正方形方格图形中，小正方形的顶点称为格点， $△ A B C$ 的顶点都在格点上，则 $∠ B A C$ 的正弦值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{1}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、5

查看试题解析
7. 如图，点B，C，D在⊙O上，若 $∠ B C D = 130 °$ ，则 $∠ B O D$ 的度数是（）

A、 $130 °$ B、 $150 °$ C、 $100 °$ D、 $120 °$

查看试题解析
8. 将抛物线y＝﹣3x²先向左平移1个单位长度，再向下平移2个单位长度，得到的抛物线的解析式是（）

A、y＝﹣3（x﹣1）²﹣2 B、y＝﹣3（x﹣1）²+2 C、y＝﹣3（x+1）²﹣2 D、y＝﹣3（x+1）²+2

查看试题解析
9. 如图，在反比例函数y= $\frac{2}{x}$ （x＞0）的图象上，有点P₁、P₂、P₃、P₄ ，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S₁、S₂、S₃ ，则S₁+S₂+S₃=（）

A、1 B、1.5 C、2 D、无法确定

查看试题解析
10. 如图抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 2$ ，与x轴一个交点在 $(- 3 ， 0)$ 和 $(- 4 ， 0)$ 之间，其部分图象如图所示.则下列结论：① $4 a - b = 0$ ；② $c < 0$ ；③ $- 3 a + c > 0$ ；④ $4 a - 2 b > a t^{2} + b t$ （t为实数）；⑤点 $(- \frac{9}{2} ， y_{1})$ ， $(- \frac{5}{2} ， y_{2})$ ， $(- \frac{1}{2} ， y_{3})$ 是该抛物线上的点，则 $y_{1} < y_{2} < y_{3}$ .正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 在△ABC中，点E，F分别是边AB，AC的中点，点D在BC边上，连接DE，DF，EF，请你添加一个条件，使△BED与△FDE全等．

查看试题解析
13. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积是．

查看试题解析
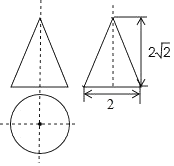14. 如图，在△ABC中，AB＝5，AC＝4，BC＝3，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB、AC于点M、N；②分别以点M、N为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点E；③作射线AE；④以同样的方法作射线BF，AE交BF于点O，连接OC，则OC＝.

查看试题解析
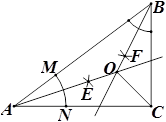15. 如图，CE是▱ABCD的边AB的垂直平分线，垂足为点O ， CE与DA的延长线交于点E ．连接AC ， BE ， DO ， DO与AC交于点F ，则下列结论：
①四边形ACBE是菱形；

②∠ACD＝∠BAE；

③AF：BE＝2：3；

④S_{四边形AFOE}：S_△COD＝2：3．

其中正确的结论有．（填写所有正确结论的序号）

查看试题解析

三、解答题

16. 计算： ${(\frac{1}{3})}^{- 1} + | \sqrt{3} - 2 | - \sqrt{12} + 6 c o s 30 ° + {(π - 3.14)}^{0}$

查看试题解析
17. 先化简： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ ，并从 $0 \leq x \leq 4$ 中选取合适的整数代入求值．

查看试题解析
18. 今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级
成绩（s）
频数（人数）
A
90＜s≤100
4
B
80＜s≤90
x
C
70＜s≤80
16
D
s≤70
6
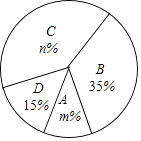
根据以上信息，解答以下问题：

(1)、表中的x=；

(2)、扇形统计图中m= ， n= ， C等级对应的扇形的圆心角为度；

(3)、该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a₁ ， a₂表示）和两名女生（用b₁ ， b₂表示），请用列表或画树状图的方法求恰好选取的是a₁和b₁的概率．

查看试题解析
19. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C.

(1)、求证：∠CBP=∠ADB.

(2)、若OA=2，AB=1，求线段BP的长.

查看试题解析
20. 如图，在东西方向的海绵线MN上，有A，B两艘巡逻船和观测点D（A，B，D在直线MN上），两船同时收到渔船C在海绵停滞点发出的求救信号．测得渔船分别在巡逻船A，B北偏西30°和北偏东45°方向，巡逻船A和渔船C相距120海里，渔船在观测点D北偏东15°方向．（说明：结果取整数．参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

(1)、求巡逻船B与观测点D间的距离；

(2)、已知观测点D处45海里的范围内有暗礁．若巡逻船B沿BC方向去营救渔船C有没有触礁的危险？并说明理由．

查看试题解析
21. 俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价40元，规定销售单价不低于44元，且获利不高于30%．试销售期间发现，当销售单价定为44元时，每天可售出300本，销售单价每上涨1元，每天销售量减少10本，现商店决定提价销售．设每天销售量为y本，销售单价为x元．

(1)、请直接写出y与x之间的函数关系式和自变量x的取值范围；

(2)、当每本足球纪念册销售单价是多少元时，商店每天获利2400元？

(3)、将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润w元最大？最大利润是多少元？

查看试题解析
22. 阅读材料：
求 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021} + 2^{2022}$ 的值．
解：设 $S = 1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021} + 2^{2022}$ ①
将①×2得： $2 S = 2 + 2 +_{2} 2^{3} + 2^{4} + ⋯ + 2^{2022} + 2^{2023}$ ②
由②－①得： $S = 2^{2023} - 1$ ，
即 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021} + 2^{2022} = 2^{2023} - 1$
请你仿照此法计算： $1 + 3 + 3^{2} + 3^{3} + ⋯ + 3^{n}$ （其中n为整数）

查看试题解析
23. 如图，抛物线y=﹣x²+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C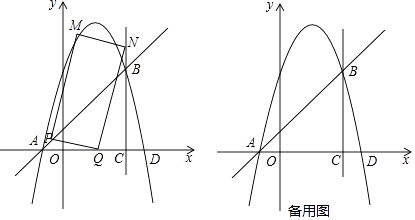

(1)、求抛物线的解析式；

(2)、点P从点A出发，以每秒 $\sqrt{2}$ 个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x=3上．
①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．

查看试题解析

等级	成绩（s）	频数（人数）
A	90＜s≤100	4
B	80＜s≤90	x
C	70＜s≤80	16
D	s≤70	6