山东省东营市垦利区2022年中考一模数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 9的算术平方根是（）

A、 3 B、－3 C、 $\sqrt{3}$ D、± $\sqrt{3}$

查看试题解析
2. 下列计算正确的是（　　）

A、a+a=2a B、b³•b³=2b³ C、a³÷a=a³ D、（a⁵）²=a⁷

查看试题解析
3. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，AB∥CD，∠A=48°，∠C=22°．则∠E等于（）

A、70° B、26° C、36° D、16°

查看试题解析
5. 某学校组织学生到社区开展公益宣传活动，成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队，如果小华和小丽每人随机选择参加其中一个宣传队，则她们恰好选到同一个宣传队的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，A（ $\sqrt{3}$ ， 1），B（1， $\sqrt{3}$ ）．将△AOB绕点O旋转150°得到△A′OB′，则此时点A的对应点A′的坐标为（）

A、（- $\sqrt{3}$ ， -1） B、（-2，0） C、（-1，- $\sqrt{3}$ ）或（-2，0） D、（- $\sqrt{3}$ ， -1）或（-2，0）

查看试题解析
7. 用一圆心角为120°，半径为6cm的扇形做成一个圆锥的侧面，这个圆锥的底面的半径是( )

A、1cm B、2cm C、3cm D、4cm

查看试题解析
8. 已知多项式x²-kx+1是一个完全平方式，则反比例函数y= $\frac{k - 1}{x}$ 的解析式为（）

A、y= $\frac{1}{x}$ B、y=- $\frac{3}{x}$ C、y= $\frac{1}{x}$ 或y=- $\frac{3}{x}$ D、y= $\frac{2}{x}$ 或y=- $\frac{2}{x}$

查看试题解析
9. 如图，在平面直角坐标系中，等腰直角三角形 $A B C$ 的顶点 $A$ 、 $B$ 分别在 $x$ 轴、 $y$ 轴的正半轴上， $∠ A B C = 90 °$ ， $C A ⊥ x$ 轴，点 $C$ 在函数 $y = \frac{k}{x} (x > 0)$ 的图象上，若 $A B = 1$ ，则 $k$ 的值为（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
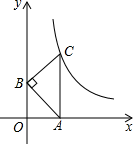10. 如图，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC＝EC，连接DF交BE的延长线于点H，连接OH交DC于点G，连接HC．则以下四个结论中正确结论的个数为（）
①OH＝BF； ②∠CHF＝45°； ③GH＝BC；④DH²＝HE·HB

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 据报道，2011年重庆主城区私家车拥有量近38000辆．将数380000用科学记数法表示为．

查看试题解析
12. 因式分解：x³-9x=.

查看试题解析
13. 如图是嘉兴市某6天内的最高气温折线统计图，则最高气温的众数是℃．

查看试题解析
14. 如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处正东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC=米（结果用根号表示）．

查看试题解析
15. 工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为mm．

查看试题解析
16. 若等腰三角形的一边长是4，另两边的长是关于 $x$ 的方程 $x^{2} - 6 x + n = 0$ 的两个根，则 $n$ 的值为．

查看试题解析
17. 如图，抛物线 $y = \frac{1}{4} x^{2} - 4$ 与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连接OQ．则线段OQ的最大值是．

查看试题解析
18. 两个反比例函数y＝ $\frac{2}{x}$ 和y＝ $\frac{4}{x}$ 在第一象限内的图象如图所示，点P₁ ， P₂ ， P₃ ， …，P₂₀₂₂在反比例函数y＝ $\frac{4}{x}$ 的图象上，它们的纵坐标分别为y₁ ， y₂ ， y₃ ， …，y₂₀₂₂ ，横坐标分别为2，4，6，…，共₂₀₂₂个偶数，过点P₁ ， P₂ ， P₃…，P₂₀₂₂分别作y轴的垂线，与y＝ $\frac{2}{x}$ 的图象交点依次为Q₁（x₁ ， y₁），Q₂（x₂ ， y₂），Q₃（x₃ ， y₃），…，Q₂₀₂₂（x₂₀₂₂ ， y₂₀₂₂），则x₂₀₂₂＝．

查看试题解析

三、解答题

19.

(1)、计算： ${(- \frac{1}{3})}^{- 1} - 3 t a n 6 0^{∘} + {(1 - \sqrt{2})}^{0} + \sqrt{12}$ ；

(2)、先化简，再求代数式 $(1 - \frac{3}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ 的值，其中x是不等式组 ${\begin{cases} x - 2 > 0 \\ 2 x + 1 < 8 \end{cases}$ 的整数解．

查看试题解析
20. 某中学为掌握学生对党史的了解情况，开展了“党在我心中”党史知识竞赛，竞赛得分为整数．王老师为了解竞赛情况，随机抽取了部分参赛学生的得分并进行整理，绘制成不完整的统计图表．
组别
成绩x/分
频数
A
75.5≤x＜80.5
6
B
80.5≤x＜85.5
14
C
85.5≤x＜90.5
m
D
90.5≤x＜95.5
n
E
95.5≤x＜100.5
p
请你根据统计图表提供的信息解答下列问题：

(1)、上表中的m= ， n= ， p=；

(2)、这次抽样调查的成绩的中位数落在哪个组？请补全频数分布直方图；

(3)、现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛，E组中的小丽和小洁是一对好朋友，请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率．

查看试题解析
21. 如图，在△ABC中，∠BAC＝30°，以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点，且 $\overset{⌢}{B C} = \overset{⌢}{C D}$ ，弦AD的延长线交切线PC于点E，连接BC．

(1)、判断OB和BP的数量关系，并说明理由；

(2)、若⊙O的半径为2，求AE的长．

查看试题解析
22. 直线 $y = x + b$ 与x轴交于点C（4，0），与y轴交于点B，并与双曲线 $y = \frac{m}{x}$ $(x < 0)$ 交于点A（-1，n）．

(1)、求直线与双曲线的解析式．

(2)、连接OA，若点D在 $x$ 轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，求出D点的坐标，若不存在，请说明理由．

查看试题解析
23. “五一”劳动节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示．

甲
乙
进价/（元/千克）
x
x+4
售价/（元/千克）
20
35
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同．

(1)、求x的值；

(2)、若超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，则超市应如何进货才能获得最大利润，最大利润是多少？

查看试题解析
24. 如图，抛物线y＝（x+1）²+k与x轴交于A、B两点，与y轴交于点C（0，﹣3）．

(1)、求抛物线的解析式；

(2)、若点M是抛物线上一动点，且在第三象限，当M点运动到何处时，四边形AMCB的面积最大？求出四边形AMCB的最大面积及此时点M的坐标．

查看试题解析
25.

(1)、【提出问题】
如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

(2)、【类比探究】
如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

(3)、【拓展延伸】
如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

查看试题解析

组别	成绩x/分	频数
A	75.5≤x＜80.5	6
B	80.5≤x＜85.5	14
C	85.5≤x＜90.5	m
D	90.5≤x＜95.5	n
E	95.5≤x＜100.5	p

	甲	乙
进价/（元/千克）	x	x+4
售价/（元/千克）	20	35