山东省东营2022年初中学业水平模拟考试数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
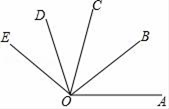
1. 下列各式正确的是( )A、 B、 C、 D、2. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
 A、50° B、60° C、70° D、80°3. 甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
A、50° B、60° C、70° D、80°3. 甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )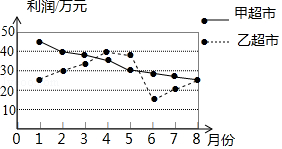 A、甲超市的利润逐月减少 B、乙超市的利润在1月至4月间逐月增加 C、8月份两家超市利润相同 D、乙超市在9月份的利润必超过甲超市4. 如图,在▱ABCD中,对角线AC,BD交于点O,∠BAC=90°,E为AB的中点,若AE=3,AO=4,则AD的长为( )
A、甲超市的利润逐月减少 B、乙超市的利润在1月至4月间逐月增加 C、8月份两家超市利润相同 D、乙超市在9月份的利润必超过甲超市4. 如图,在▱ABCD中,对角线AC,BD交于点O,∠BAC=90°,E为AB的中点,若AE=3,AO=4,则AD的长为( )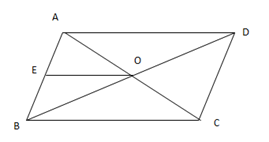 A、10 B、12 C、 D、5. 如图,在中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是( )
A、10 B、12 C、 D、5. 如图,在中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是( )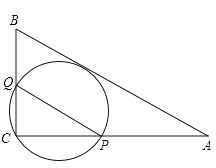 A、4.75 B、4.8 C、5 D、6. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
A、4.75 B、4.8 C、5 D、6. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )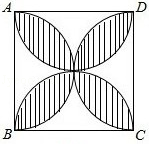 A、 B、 C、 D、7. 如图,在正方形ABCD中,点E、F分别是边BC和CD上的两点,若AB=1,△AEF为等边三角形,则CE=( )
A、 B、 C、 D、7. 如图,在正方形ABCD中,点E、F分别是边BC和CD上的两点,若AB=1,△AEF为等边三角形,则CE=( ) A、 B、 C、 D、8. 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB= , BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E,设AP=x,DE=y,在下列图象中,能正确反映y与x的函数关系的是( )
A、 B、 C、 D、8. 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB= , BC=2,P是BC边上的一个动点(点P与点B不重合),DE⊥AP于点E,设AP=x,DE=y,在下列图象中,能正确反映y与x的函数关系的是( ) A、
A、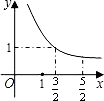 B、
B、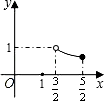 C、
C、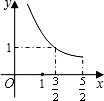 D、
D、 9. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac<b2;②2a-b<0;③4a+c>2b;④3b+2c<0;⑤m(am+b)<a-b(m≠﹣1),其中正确结论的个数是( )
9. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac<b2;②2a-b<0;③4a+c>2b;④3b+2c<0;⑤m(am+b)<a-b(m≠﹣1),其中正确结论的个数是( )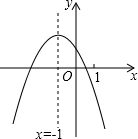 A、4个 B、3个 C、2个 D、1个10. 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
A、4个 B、3个 C、2个 D、1个10. 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )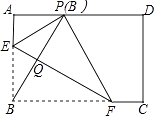 A、①② B、②③ C、①③ D、①④
A、①② B、②③ C、①③ D、①④二、填空题
-
11. 某公益机构设立了网站接受爱心捐助,旨在推动社会和谐,发展公益慈善事业,据网站统计,目前已有大约2451000人献爱心,将“2451000”用科学记数法表示是.12. 因式分解+2x-3= .13. 小明用公式S2=计算一组数据x1 , x2 , …xn的方差,那么这组数据的和是 .14. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .15. 如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为 .
 16. 如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知⊙O是△ABC的内切圆,则阴影部分面积为 .
16. 如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知⊙O是△ABC的内切圆,则阴影部分面积为 .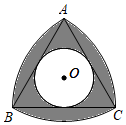 17. 如图,已知平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是.
17. 如图,已知平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是.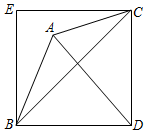 18. 如图,在平面直角坐标系中,直线l2:与x轴交于点A;与y轴交于点B,以x轴为对称轴作直线的轴对称图形的直线l2 , 点A1 , A2 , A3…在直线l1上,点B1 , B2 , B3…在x正半轴上,点C1 , C2 , C3…在直线l2上,若△A1B1O、△A2B2B1、△A2B1B2、…△AnBnBn﹣1均为等边三角形,四边形A1B1C1O、四边形A2B2C2B1、四边形A2B1C2B2…、四边形AnBn∁nBn﹣1的面积分别是S1、S2、S3、…、Sn , 则Sn为 . (用含有n的代数式表示)
18. 如图,在平面直角坐标系中,直线l2:与x轴交于点A;与y轴交于点B,以x轴为对称轴作直线的轴对称图形的直线l2 , 点A1 , A2 , A3…在直线l1上,点B1 , B2 , B3…在x正半轴上,点C1 , C2 , C3…在直线l2上,若△A1B1O、△A2B2B1、△A2B1B2、…△AnBnBn﹣1均为等边三角形,四边形A1B1C1O、四边形A2B2C2B1、四边形A2B1C2B2…、四边形AnBn∁nBn﹣1的面积分别是S1、S2、S3、…、Sn , 则Sn为 . (用含有n的代数式表示)
三、解答题
-
19. 计算:(1)、+(2)、先化简,再求代数式的值,其中 .20. 今年6月份,永州市某中学开展“六城同创”知识竞赛活动.赛后,随机抽取了部分参赛学生的成绩,按得分划为A,B,C,D四个等级,A: , B: , C: , D: , 并绘制了如下两幅不完整的统计图,请结合图中所给信息,解答下列问题:
 (1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、该校准备从上述获得A等级的四名学生中选取两人参加永州市举行的“六城同创”知识竞赛,已知这四人中有两名男生(用 , 表示),两名女生(用 , 表示),请利用树状图法或列表法,求恰好抽到1名男生和1名女生的概率.21. 如图,已知 是⊙O的直径,⊙O经过 的直角边 上的点F,交 边于点E,点F是弧 的中点, ,连接 .
(1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、该校准备从上述获得A等级的四名学生中选取两人参加永州市举行的“六城同创”知识竞赛,已知这四人中有两名男生(用 , 表示),两名女生(用 , 表示),请利用树状图法或列表法,求恰好抽到1名男生和1名女生的概率.21. 如图,已知 是⊙O的直径,⊙O经过 的直角边 上的点F,交 边于点E,点F是弧 的中点, ,连接 . (1)、求证:直线 是⊙O切线.(2)、若 , ,求 的值.22. 如图所示,直线y=x+b与双曲线y=交与A,B两点,已知点B的纵坐标为-3,直线AB与x轴交于点C,与y轴交与点D(0,2),OA= , = ,
(1)、求证:直线 是⊙O切线.(2)、若 , ,求 的值.22. 如图所示,直线y=x+b与双曲线y=交与A,B两点,已知点B的纵坐标为-3,直线AB与x轴交于点C,与y轴交与点D(0,2),OA= , = , (1)、求直线AB的解析式.(2)、若点P是第二象限内反比例函数图象上的一点,△OCP的面积是面积的2倍,求点P的坐标.(3)、直接写出不等式x+b≤的解集.23. 某文具店经营某种品牌的文具盒,购进时的单价是30元,根据统计调查:在一段时间内,销售单价是40元时,文具盒销售量是600个,而销售单价每涨2元,就会少售出20个文具盒.(1)、不妨设该种品牌文具盒的销售单价为元(),请你分别用的代数式来表示销售量个和销售该品牌文具盒获得利润元,并把结果填写在表格中:
(1)、求直线AB的解析式.(2)、若点P是第二象限内反比例函数图象上的一点,△OCP的面积是面积的2倍,求点P的坐标.(3)、直接写出不等式x+b≤的解集.23. 某文具店经营某种品牌的文具盒,购进时的单价是30元,根据统计调查:在一段时间内,销售单价是40元时,文具盒销售量是600个,而销售单价每涨2元,就会少售出20个文具盒.(1)、不妨设该种品牌文具盒的销售单价为元(),请你分别用的代数式来表示销售量个和销售该品牌文具盒获得利润元,并把结果填写在表格中:销售单价(元)
销售量(个)
销售文具盒获得利润(元)
(2)、在(1)问条件下,若该文具店获得了6000元销售利润,求该文具盒销售单价应定为多少元?(3)、在(1)问条件下,若厂家规定该品牌文具盒销售单价不低于44元,且文具店要完成不少于380个的销售目标,求该文具店销售该品牌文具盒获得的最大利润是多少元?24. 如图,抛物线与轴相交于、两点,与轴相交于点 , 且点与点的坐标分别为 , 点是抛物线的顶点.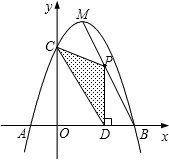 (1)、求二次函数的关系式;(2)、点为线段上一个动点,过点作轴于点 , 若 , 的面积为 , 求与的函数关系式,并求当取得最大值时,点的坐标;(3)、在上是否存在点 , 使为直角三角形?如果存在,请直接写出点的坐标;如果不存在,请说明理由.25.(1)、阅读理解:
(1)、求二次函数的关系式;(2)、点为线段上一个动点,过点作轴于点 , 若 , 的面积为 , 求与的函数关系式,并求当取得最大值时,点的坐标;(3)、在上是否存在点 , 使为直角三角形?如果存在,请直接写出点的坐标;如果不存在,请说明理由.25.(1)、阅读理解:
如图1,在正方形ABCD中,若E,F分别是CD,BC边上的点,∠EAF=45°,则我们常会想到:把△ADE绕点A顺时针旋转90°得到△ABG.易证△AEF≌ , 得出线段BF,DE,EF之间的数量关系为;
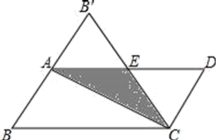
(2)、类比探究:如图2,在等边△ABC中,D,E为BC边上的点,∠DAE=30°,BD=3,EC=4,求线段DE的长;
(3)、拓展应用如图3,在△ABC中,AB=AC,∠BAC=150°,点D,E在BC边上,∠DAE=75°,若DE是等腰△ADE的腰长,请直接写出BD:CE的值.