辽宁省锦州市2022年九年级下学期学情摸底数学试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 实数4的算术平方根是( )A、 B、± C、2 D、±22. 目前代表华为手机最强芯片的麒麟990处理器采用7nm工艺制造,已知1nm=10−3um,1um=10−3mm,则7nm等于( )A、 B、 C、 D、3. 如图所示的几何体的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列因式分解正确的是( )A、 B、 C、 D、5. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 . 后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变6. 抛物线y=ax2+bx+c向右平移5个单位,再向上平移1个单位,得到的抛物线的解析式为y=-3(x-1)2+4,则抛物线y=ax2+bx+c的顶点坐标是( )
4. 下列因式分解正确的是( )A、 B、 C、 D、5. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 . 后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变6. 抛物线y=ax2+bx+c向右平移5个单位,再向上平移1个单位,得到的抛物线的解析式为y=-3(x-1)2+4,则抛物线y=ax2+bx+c的顶点坐标是( )
A、(6,3) B、(6,5) C、(-4,3) D、(-4,5)7. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( ) A、1 B、 C、 D、8. 已知等腰直角的斜边AB= , 正方形DEFG的边长为 , 把和正方形DEFG如图放置,点B与点E重合,边AB与EF在同一条直线上,将沿AB方向以每秒个单位的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是( )
A、1 B、 C、 D、8. 已知等腰直角的斜边AB= , 正方形DEFG的边长为 , 把和正方形DEFG如图放置,点B与点E重合,边AB与EF在同一条直线上,将沿AB方向以每秒个单位的速度匀速平行移动,当点A与点E重合时停止移动.在移动过程中,与正方形DEFG重叠部分的面积S与移动时间t(s)的函数图象大致是( ) A、
A、 B、
B、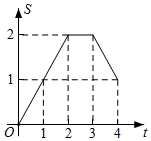 C、
C、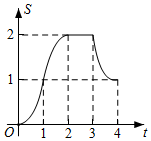 D、
D、
二、填空题
-
9. 函数y= 中自变量x的取值范围是 .
10. 在一个不透明的布袋中装有18个白球和若干个黑球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到白球的概率是 , 则黑球的个数为 .11. 如图,在 中, , , ,将 绕点 顺时针旋转,使斜边 过 点,则线段 扫过的面积为.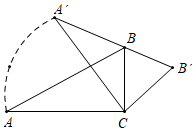 12. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC= .
12. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC= . 13. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是 .14. 如图,在△ABC中,∠ACB=90°,∠A=60°,以点A为圆心,以小于AC的长为半径作弧,分别交AC于点D,交AB于点E,再分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线AF交BC于点G、连接EG.则 .
13. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是 .14. 如图,在△ABC中,∠ACB=90°,∠A=60°,以点A为圆心,以小于AC的长为半径作弧,分别交AC于点D,交AB于点E,再分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线AF交BC于点G、连接EG.则 . 15. 如图,是反比例函数图象上的两点,过点作轴,垂足为 , 交于点D,且为的中点,若的面积为6,则的值为 .
15. 如图,是反比例函数图象上的两点,过点作轴,垂足为 , 交于点D,且为的中点,若的面积为6,则的值为 . 16. 如图,A1 , A2 , ⋯⋯在直线上,B1 , B2 , ⋯⋯在直线上,OA1= , 四边形AnBnCnAn+1为正方形,则四边形AnBnCnAn+1的面积是 .
16. 如图,A1 , A2 , ⋯⋯在直线上,B1 , B2 , ⋯⋯在直线上,OA1= , 四边形AnBnCnAn+1为正方形,则四边形AnBnCnAn+1的面积是 .
三、解答题
-
17. 先化简,再求值. ,其中 .18. 为庆祝中国共产党建党100周年,某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛,现随机抽取部分学生的成绩分成A、B、C、D、E五个等级进行统计,并绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
 (1)、本次调查中共抽取多少名学生?(2)、补全条形统计图;(3)、在扇形统计图中,求B等级所对应的扇形圆心角的度数;(4)、若该校有1200名学生参加此次竞赛,估计这次竞赛成绩为A和B等级的学生共有多少名?19. 为弘扬中华民族传统文化,某市举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小华参加“单人组”,他从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小明和小红组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次.则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少?小明和小红都没有抽到“三字经”的概率是多少?请用画树状图或列表的方法进行说明.20. 小张从A地出发去相距4.5千米的B地上班,他每天出发的时间都相同.第一天步行去上班结果迟到了5分钟.第二天骑自行车去上班结果早到10分钟.已知骑自行车的速度是步行速度的1.5倍.求小张每小时步行的速度和骑自行车的速度是多少?21. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )
(1)、本次调查中共抽取多少名学生?(2)、补全条形统计图;(3)、在扇形统计图中,求B等级所对应的扇形圆心角的度数;(4)、若该校有1200名学生参加此次竞赛,估计这次竞赛成绩为A和B等级的学生共有多少名?19. 为弘扬中华民族传统文化,某市举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小华参加“单人组”,他从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小明和小红组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次.则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少?小明和小红都没有抽到“三字经”的概率是多少?请用画树状图或列表的方法进行说明.20. 小张从A地出发去相距4.5千米的B地上班,他每天出发的时间都相同.第一天步行去上班结果迟到了5分钟.第二天骑自行车去上班结果早到10分钟.已知骑自行车的速度是步行速度的1.5倍.求小张每小时步行的速度和骑自行车的速度是多少?21. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )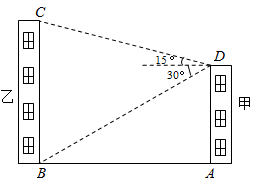 22. 如图,已知△ABC,O为AC上一点,⊙O与BC相切于点C,射线BO交⊙O于点M,过点A作AD⊥BM垂足为D点,交⊙O于F、G两点,且∠AOD=∠BAD.
22. 如图,已知△ABC,O为AC上一点,⊙O与BC相切于点C,射线BO交⊙O于点M,过点A作AD⊥BM垂足为D点,交⊙O于F、G两点,且∠AOD=∠BAD.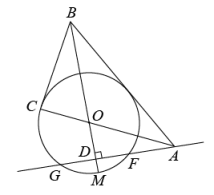 (1)、求证:AB为⊙O的切线:(2)、若BC=6,tan∠ABC= , 求AD的长.23. 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?24. 如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D,E分别在AC,BC边上,DC=EC,连接DE,AE,BD,点M,N,P分别是AE,BD,AB的中点,连接PM、PN、MN.
(1)、求证:AB为⊙O的切线:(2)、若BC=6,tan∠ABC= , 求AD的长.23. 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?24. 如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D,E分别在AC,BC边上,DC=EC,连接DE,AE,BD,点M,N,P分别是AE,BD,AB的中点,连接PM、PN、MN. (1)、BE与MN的数量关系是;
(1)、BE与MN的数量关系是;
(2)、将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
 (3)、若CB=6,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B,E,D三点在一条直线上时,MN的长度为 .25. 如图,抛物线与轴交于点A(-2,0)、B(4,0),与y轴交于点C,过点C作轴的平行线交抛物线于点D,连接AC,作直线BC.
(3)、若CB=6,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B,E,D三点在一条直线上时,MN的长度为 .25. 如图,抛物线与轴交于点A(-2,0)、B(4,0),与y轴交于点C,过点C作轴的平行线交抛物线于点D,连接AC,作直线BC. (1)、求抛物线的表达式;(2)、如图2,点E( , 0)是线段OB上的点,过点E作与轴垂直的直线与直线BC交于点F,与抛物线交于点G.
(1)、求抛物线的表达式;(2)、如图2,点E( , 0)是线段OB上的点,过点E作与轴垂直的直线与直线BC交于点F,与抛物线交于点G.①线段FG的长是否存在最大值?若存在,求出这个最大值:若不存在,说明理由;
②连接CG,当∠DCG=∠ACO时,求点G的坐标;
(3)、若点P是直线BC下方的抛物线上的一点,点Q在y轴上,点M在线段BC上,当以C,P,Q,M为顶点的四边形是菱形时,直接写出菱形的边长.