辽宁省葫芦岛市龙港区2022年第二次模拟考试数学试题

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. “垃圾分一分，环境美十分”下列四种垃圾回收标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y=x²+2的顶点坐标是（）

A、（1，﹣2） B、（1，2） C、（0，﹣2） D、（0，2）

查看试题解析
3. 如图，点A，B，C是⊙O上的点，∠AOB=70°，则∠ACB的度数是（）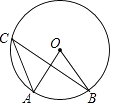

A、30° B、35° C、45° D、70°

查看试题解析
4. 图示为抛物线y＝ax²+bx+c的一部分，其对称轴为直线x＝2，若其与x轴的一交点为B（6，0），则由图象可知，不等式ax²+bx+c＞0的解集是（）

A、x＞6 B、0＜x＜6 C、﹣2＜x＜6 D、x＜﹣2或x＞6

查看试题解析
5.
如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

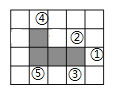查看试题解析
6. 四张完全相同的卡片上，分别画有等边三角形、矩形、菱形、正五边形，现从中随机抽取一张，卡片上画的恰好是中心对称图形的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
7. 若一个口袋中装有2个红球和一个黑球，对于“从中摸出一个球是红球”这个事件，下列说法正确的是（）

A、发生的可能性为 $\frac{1}{3}$ B、是不可能事件 C、随机事件 D、必然事件

查看试题解析
8. 关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个实数根，则k的取值范围（）

A、 $k \geq - 1$ B、 $k \leq - 1$ C、 $k > - 1 且 k \neq 0$ D、 $k \geq - 1 且 k \neq 0$

查看试题解析
9. 已知二次函数的图象与x轴有两个交点，且顶点坐标为（﹣2，1）．若函数图象经过（1，y₁），（﹣1，y₂），（﹣4，y₃）三点，则（）

A、y₁＜y₃＜y₂ B、y₂＜y₁＜y₃ C、y₁＜y₂＜y₃ D、y₂＜y₃＜y₁

查看试题解析
10. 如图，已知点A（﹣1，0）和点B（1，1），若抛物线y＝x²＋c与线段AB有公共点，则c的取值范围是（）

A、﹣1≤c≤0 B、﹣1≤c≤ $\frac{1}{2}$ C、﹣1≤c≤ $\frac{9}{16}$ D、0≤c≤ $\frac{9}{16}$

查看试题解析

二、填空题

11. 抛物线 $y = (x + 2)^{2} - 1$ 的对称轴是．

查看试题解析
12. 在“绿水青山就是金山银山”这句话中任选一个汉字，这个字是“山”的概率.

查看试题解析
13. 一个圆锥的侧面展开图是一个圆心角为216°、半径为15cm的扇形，这个圆锥的底面圆半径为cm．

查看试题解析
14.
如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是．

查看试题解析
15. 如图，△ODC是由△OAB绕点O顺时针旋转40°后得到的图形，若点D恰好落在AB上，且∠AOC=105°，则∠C=°.

查看试题解析
16. 如图，圆与圆的位置关系有．

查看试题解析
17. 若 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2020 x + 1 = 0$ 的两个实数根，则代数式 $(x_{1} + 1) (x_{2} + 1)$ 的值等于．

查看试题解析
18. 如图，△ABC是边长为3的等边三角形，E在AC上且AE=2，D是直线BC_上一动点，线段ED绕点E逆时针旋转90°，得到线段EF，连接DF，AF，下列结论：①DF的最小值为 $\frac{\sqrt{6}}{2}$ ；②AF的最小值是 $1 + \frac{\sqrt{3}}{2}$ ；③当CD=1时， $D E ∥ A B$ ；④当 $D E ∥ A B$ 时，DE=1．正确结论的题号是．

查看试题解析

三、解答题

19. 用如图所示的两个转盘（分别进行四等分和三等分），设计一个“配紫色”的游戏，分别转动两个转盘（指针指向区域分界线时，忽略不计），若其中一个转出红色，另一个转出蓝色即可配成紫色，求可配成紫色的概率．

查看试题解析
20. 如图，点 $A (2 ， 3)$ ， $B (4 ， 3)$ ， $C (1 ， 1)$ ，将△ABC绕原点O顺时针旋转90°得 $△ A_{1} B_{1} C_{1}$ ．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、求点B在旋转过程中经过的路径长；

(3)、直接写出线段AB扫过的图形面积．

查看试题解析
21. 一个黑箱子里装有红、白两种颜色的球4只，他们除颜色外，其他都相同，小明将球搅匀后从箱子中随机摸出一个球，记下颜色，再把它放回不断重复实验，将多次实验结果画出如下频率统计图.

(1)、当摸球次数很大时，摸到白球的频率将会接近（精确到0.01），从箱子中摸一次球，摸到红球的概率是；

(2)、从该箱子里随机摸出一个球，不放回，再摸出一个球.用树状图或列表法求出摸到一个红球一个白球的概率.

查看试题解析
22. 如图，△ABC是等边三角形，AB=4，以AB为直径作 $⊙ O$ ，交BC边于点D，交AC边于点F，DE与 $⊙ O$ 相切交AC于E，求由DE，EF和 $\overset{⌢}{D F}$ 围成的阴影部分的面积．

查看试题解析
23. 如图，AB是 $⊙ O$ 的直径，弦CD⊥AB，垂足为E，F在AB延长线上，连接CF，CB，∠FCB=∠BCD．

(1)、求证：CF为 $⊙ O$ 的切线；

(2)、若BE=4，FB=6，求 $⊙ O$ 的半径．

查看试题解析
24. 某服装厂批发应季T恤衫，其单价y（元）与一次批发数量x（件）（x为正整数）之间的关系满足图中折线的函数关系．

(1)、求y与x的函数关系式；

(2)、若每件T恤衫的成本价是60元，当 $100 < x \leq 400$ 时，求服装厂所获利润w（元）与x（件）之间的函数关系式，并求一次批发多少件时所获利润最大，最大利润是多少？

查看试题解析
25. 如图，在△ABC中，AB=AC，∠BAC=90°，AH⊥BC，H为垂足，将△ABH绕点A逆时针旋转 $α$ 得△ADE，连接CD，F为CD的中点，连接FH，FE．

(1)、求证：FH=FE且FH⊥FE；

(2)、若AB=4， $α = 180 °$ ，直接写出点F经过的路径长．

查看试题解析
26. 如图，抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C，直线 $y = \frac{1}{2} x + 1$ 与x轴交于点E，与y轴交于点D．

(1)、求抛物线的解析式；

(2)、P为抛物线上的点，连接OP交直线DE于Q，当Q是OP中点时，求点P的坐标；

(3)、M在直线DE上，当△CDM为等腰三角形时，直接写出点M的坐标．

查看试题解析