辽宁省鞍山市立山区2022年九年级上学期数学一模试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 平面直角坐标系内与点 关于原点对称的点的坐标是( )A、 B、 C、 D、2. 方程(x﹣1)(x+2)=2(x+2)的根是( )A、1,﹣2 B、3,﹣2 C、3 D、13. 如图,在 中,D、E分别是AB和AC的中点, ,则 ( )
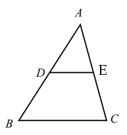 A、30 B、25 C、22.5 D、204. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )
A、30 B、25 C、22.5 D、204. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )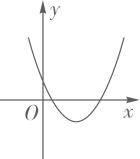 A、
A、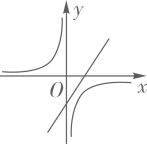 B、
B、 C、
C、 D、
D、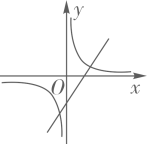 5. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= , CE=1,则弧BD的长是( )
5. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= , CE=1,则弧BD的长是( )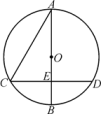 A、 B、 C、 D、6. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A、 B、 C、 D、6. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )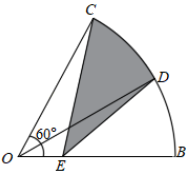 A、 B、 C、 D、8. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:
A、 B、 C、 D、8. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:①a+b+c=0;②a﹣2b+c>0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤a﹣b<m(am+b)(m为任意实数).
其中正确的结论有( )
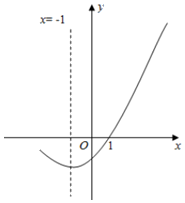 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 已知二次函数(为常数)的图象与轴的一个交点为 , 则关于的一元二次方程的两实数根是 .10. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1∶3,点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为.
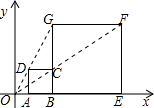 11. 如图,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为.
11. 如图,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为.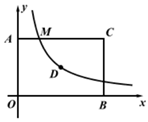 12. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为.
12. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为.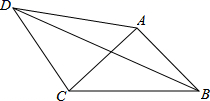 13. 如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m²,设道路的宽为x m,则根据题意,可列方程为.
13. 如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m²,设道路的宽为x m,则根据题意,可列方程为.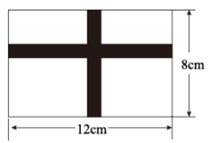 14. 如图,在 中, , , .若以 所在直线为轴,把 旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.
14. 如图,在 中, , , .若以 所在直线为轴,把 旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.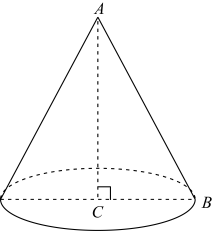 15. 若 , 是一元二次方程的两个实数根,则的值为 .16. 如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 , 且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2 , 且A2O=2A1O……,依此规律,得到等腰直角三角形A2021OB2021 , 则点B2021的坐标为 .
15. 若 , 是一元二次方程的两个实数根,则的值为 .16. 如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 , 且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2 , 且A2O=2A1O……,依此规律,得到等腰直角三角形A2021OB2021 , 则点B2021的坐标为 .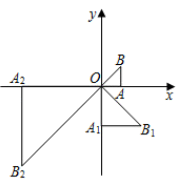
三、解答题
-
17. 关于x的一元二次方程x2+(k+3)x+3k=0.(1)、求证:方程总有两个实数根;(2)、选取一个合适的k值,使得方程有两个整数根,并求出这两个整数根.18. 如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫做格点, 为平面直角坐标系的原点,矩形 的4个顶点均在格点上,连接对角线 .
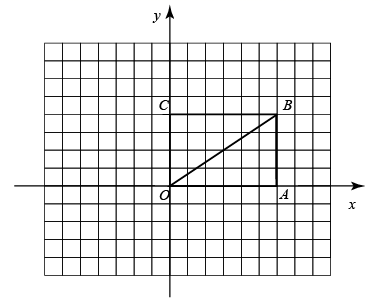
⑴在平面直角坐标系内,以原点 为位似中心,把 缩小,作出它的位似图形,并且使所作的位似图形与 的相似比等于 ;
⑵将 以 为旋转中心,逆时针旋转 ,得到 ,作出 ,并求出线段 旋转过程中所形成扇形的周长.
19. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .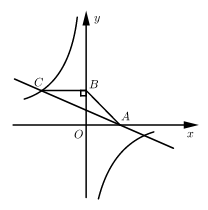 (1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.20. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.20. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.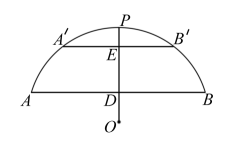 (1)、求所在圆的半径r的长;(2)、当洪水上升到跨度只有30米时,要采取紧急措施.若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?并说明理由.21. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.
(1)、求所在圆的半径r的长;(2)、当洪水上升到跨度只有30米时,要采取紧急措施.若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?并说明理由.21. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.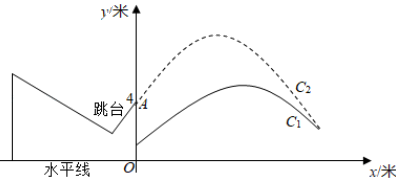 (1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?22. 如图,在矩形 中,E是 的中点, ,垂足为F.
(1)、当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?22. 如图,在矩形 中,E是 的中点, ,垂足为F.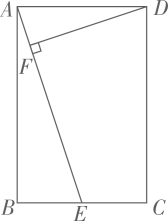 (1)、求证: ;(2)、若 , ,求 的长.23. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC.
(1)、求证: ;(2)、若 , ,求 的长.23. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC.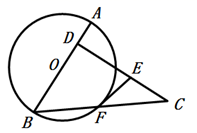 (1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.24. 某商户把一批糖果分装成小袋出售,小袋糖果成本为2.5元/袋,试销发现:每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系y=﹣20x+190,其中3≤x≤5.(1)、当销售单价为多少元时,每天销售获得165元的利润?(2)、设每天所获利润为W元,当销售单价为多少元时,每天获得的利润最大?最大利润是多少元?25. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.24. 某商户把一批糖果分装成小袋出售,小袋糖果成本为2.5元/袋,试销发现:每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系y=﹣20x+190,其中3≤x≤5.(1)、当销售单价为多少元时,每天销售获得165元的利润?(2)、设每天所获利润为W元,当销售单价为多少元时,每天获得的利润最大?最大利润是多少元?25. 在 , , .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.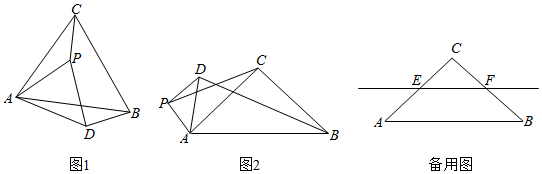 (1)、观察猜想
(1)、观察猜想如图1,当 时, 的值是 , 直线BD与直线CP相交所成的较小角的度数是.
(2)、类比探究如图2,当 时,请写出 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)、解决问题当 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时 的值.
26. 已知抛物线y=ax2+2x+c过A(﹣1,0),C(0,3),交x轴于另一点B.点P是抛物线上一动点(不与点C重合),直线CP交抛物线对称轴于点N.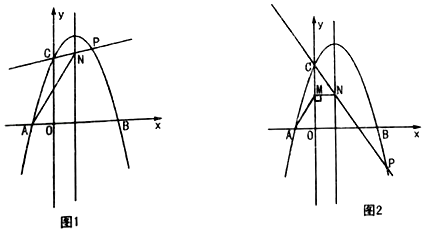 (1)、求抛物线的解析式;(2)、连接AN,当∠ANC=45°时,求P点的横坐标;(3)、如图2,过点N作NM⊥y轴于点M,连接AM,当AM+MN+CN的值最小时,直接写出N点的坐标.
(1)、求抛物线的解析式;(2)、连接AN,当∠ANC=45°时,求P点的横坐标;(3)、如图2,过点N作NM⊥y轴于点M,连接AM,当AM+MN+CN的值最小时,直接写出N点的坐标.