黑龙江省哈尔滨市南岗区2022年中考数学模拟练习试题
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 我市4月份某天的最高气温是 , 最低气温是 , 那么这天的温差(最高气温减最低气温)是( ).A、 B、 C、 D、2. 下列运算正确的是( ).A、 B、 C、 D、3. 如图是几个小正方体组成的一个几何体,这个几何体的俯视图是( )
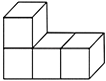 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,既是轴对称图形,又是中心对称图形的是( ).A、
4. 下列图形中,既是轴对称图形,又是中心对称图形的是( ).A、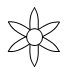 B、
B、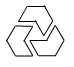 C、
C、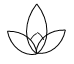 D、
D、 5. 在反比例函数图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ).A、 B、 C、 D、6. 将抛物线向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线的解析式为( )A、 B、 C、 D、7.
5. 在反比例函数图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ).A、 B、 C、 D、6. 将抛物线向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线的解析式为( )A、 B、 C、 D、7.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
 A、2海里 B、2sin55°海里 C、2cos55°海里 D、2tan55°海里8. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人.则选出的恰为一男一女的概率是( )A、 B、 C、 D、9. 如图,在中,平分 , 若 , 则的面积为( )
A、2海里 B、2sin55°海里 C、2cos55°海里 D、2tan55°海里8. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人.则选出的恰为一男一女的概率是( )A、 B、 C、 D、9. 如图,在中,平分 , 若 , 则的面积为( ) A、6 B、18 C、24 D、3210. 如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论不正确的是( )
A、6 B、18 C、24 D、3210. 如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数据65200用科学记数法表示为 .12. 函数y= 中,自变量x的取值范围是 .13. 计算: .14. 因式分解:4ax2+16axy+16ay2= .15. 不等式组 的最大整数解为 .16. 一个扇形的面积为12πcm2 , 圆心角为120°,则该扇形的半径是.17. 某超市今年一月份的营业额为60万元.三月份的营业额为135万元.若每月营业额的平均增长,则二月份的营业额是万元.
18. 如图,在中, , 点D在边上, , 把绕着点D逆时针旋转度后,如果点B恰好落在初始的边上,那么 . 19. 如图,内接于的半径为6,于点 , 则的长为 .
19. 如图,内接于的半径为6,于点 , 则的长为 . 20. 如图,四边形中, , 连接于点 , , 则的长为 .
20. 如图,四边形中, , 连接于点 , , 则的长为 .
三、解答题
-
21. 先化简,再求代数式的值,其中22. 如图,方格纸中每个小正方形的边长均为1,线段的两个端点均在小正方形的顶点上.
 (1)、在图中画出以为一条边的平行四边形 , 且这个平行四边形的周长为22,点C、点D均在小正方形的顶点上;(2)、在图中画出以为一边的等腰 , 点E在小正方形的顶点上,且使的面积最大,并直接写出此时的最大面积.23. 某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图,请根据图中提供的信息解答下列问题:
(1)、在图中画出以为一条边的平行四边形 , 且这个平行四边形的周长为22,点C、点D均在小正方形的顶点上;(2)、在图中画出以为一边的等腰 , 点E在小正方形的顶点上,且使的面积最大,并直接写出此时的最大面积.23. 某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图,请根据图中提供的信息解答下列问题: (1)、本次共调查了多少名学生;(2)、通过计算补全频数分布直方图;(3)、请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.24. 已知:在矩形中,把矩形绕点C旋转,得到矩形 , 且点E落在边上,连接交于点H.
(1)、本次共调查了多少名学生;(2)、通过计算补全频数分布直方图;(3)、请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.24. 已知:在矩形中,把矩形绕点C旋转,得到矩形 , 且点E落在边上,连接交于点H. (1)、如图1,求证:;(2)、如图2,连接 , 若平分 , 在不添加任何辅助线的条件下,请直接写出图2中所有数量关系为2倍的两条线段.25. 某中学为了创建书香校园,去年购买了一批图书,其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和科普书的单价各是多少元?(2)、若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,这所中学今年计划再购买文学书和科普书共200本,且购买文学书和科普书的总费用不超过2135元,这所中学今年至少要购买多少本文学书?
(1)、如图1,求证:;(2)、如图2,连接 , 若平分 , 在不添加任何辅助线的条件下,请直接写出图2中所有数量关系为2倍的两条线段.25. 某中学为了创建书香校园,去年购买了一批图书,其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和科普书的单价各是多少元?(2)、若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,这所中学今年计划再购买文学书和科普书共200本,且购买文学书和科普书的总费用不超过2135元,这所中学今年至少要购买多少本文学书?

