人教版数学八年级下册第十九章19.2一次函数
试卷更新日期:2022-04-25 类型:同步测试
一、单选题
-
1. 若点在函数的图象上,则下列各点中也在该函数图象上的是( )A、(4,2) B、(2,4) C、(1,2) D、(﹣4,2)2. 一次函数y=8x的图象经过的象限是( )A、一、三 B、二、四 C、一、三、四 D、二、三、四3. 将直线y=﹣3x沿着x轴向右平移2个单位,所得直线的解析式为( )A、y=﹣3x+2 B、y=﹣3x﹣2 C、y=﹣3x﹣6 D、y=﹣3x+64. 若一次函数y=kx+b(k,b为常数,k≠0)的图象经过点A(0,-1)和B(1,1),则不等式kx+b>1的解集为( )A、x<0 B、x>0 C、x<1 D、x>15. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
 B、
B、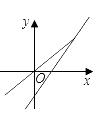 C、
C、 D、
D、 6. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.
6. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则18分钟时的温度是( )
A、62℃ B、64℃ C、66℃ D、68℃7. 在平面直角坐标系中,若点(x1 , -1),(x2 , -2),(x3 , 1)都在直线y=-2x+b上,则x1 , x2 , x3的大小关系是( )A、x1>x2>x3 B、x3>x2>x1 C、x2>x1>x3 D、x2>x3>x18. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行9. 一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( ) A、x=2 B、y=2 C、x=-1 D、y=-110. 直线y=-2x+4与两坐标轴围成的三角形的面积是( )A、4 B、6 C、8 D、16
A、x=2 B、y=2 C、x=-1 D、y=-110. 直线y=-2x+4与两坐标轴围成的三角形的面积是( )A、4 B、6 C、8 D、16二、填空题
-
11. 若一次函数y=2x﹣3的图象经过点A(a,1),则a=.12. 小明从家步行到学校需走的路程为2000米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行20分钟时,距离学校还有米.
 13. 已知一次函数y=ax+b和y=kx的图象交于点P(﹣4,2),则关于x、y的二元一次方程组 的解是.14. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费y(元)与行李质量 之间满足一次函数关系,部分对应值如下表:
13. 已知一次函数y=ax+b和y=kx的图象交于点P(﹣4,2),则关于x、y的二元一次方程组 的解是.14. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费y(元)与行李质量 之间满足一次函数关系,部分对应值如下表:…
30
40
50
…
y(元)
…
4
6
8
…
则旅客最多可免费携带行李的质量是kg.
15. 如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 . 16. 下列函数:①y=2x-8;②y=-2x+8:③y=2x+8;④y=-2x-8.其中,y随x的增大而减小的函数是(填序号).
16. 下列函数:①y=2x-8;②y=-2x+8:③y=2x+8;④y=-2x-8.其中,y随x的增大而减小的函数是(填序号).三、解答题
-
17. 已知 , 并且与x成正比例,与成反比例.当时,;当时, , 求:y关于x的函数解析式.18. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.
 (1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.
(1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.

