人教版数学八年级下册第十九章19.1变量与函数
试卷更新日期:2022-04-25 类型:同步测试
一、单选题
-
1. 圆的周长公式是 ,那么在这个公式中,关于变量和常量的说法正确的是( )A、2是常量,C、π、r是变量 B、2、π是常量,C、r是变量 C、2、C是常量,r、π是变量 D、2、π、r是常量,C是变量
-
2. 某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为 ( )A、9 ℃ B、7 ℃ C、6 ℃ D、3 ℃
-
3. 笔记本每本a元,买3本笔记本共支出y元,下列选项判断正确的有( )A、a是常量时,y是变量 B、a是变量时,y是常量 C、a是变量时,y也是变量 D、无论a是常量还是变量、y都是变量
-
4. 下列图象中, 不是 的函数的是( )A、
 B、
B、 C、
C、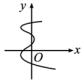 D、
D、
-
5. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A、在这个变化中,自变量是温度,因变量是声速 B、温度越高,声速越快 C、当空气温度为20℃时,声音5s可以传播1740m D、当温度每升高10℃,声速增加6m/s -
6. 在关系式 中,当自变量 时,因变量y的值为( ).A、22 B、25 C、18 D、11
-
7. 函数y= 中,自变量x的取值范围是( )A、x≤5 B、x<5 C、x≥5 D、x>5
-
8. 如图所示,有一个容器水平放置,往此容器内注水,注满为止.若用h(单位:cm)表示容器底面到水面的高度,用V(单位:)表示注入容器内的水量,则表示V与h的函数关系的图象大致是( )
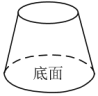 A、
A、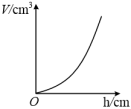 B、
B、 C、
C、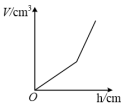 D、
D、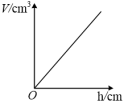
-
9. 下列关于变量x,y的关系,其中y不是x的函数的是( )A、
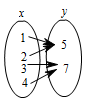 B、
B、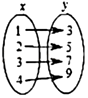 C、
C、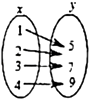 D、
D、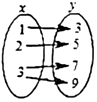
-
10. 一次函数 的自变量的取值增加2,函数值就相应减少4,则k的值为( )A、2 B、-1 C、-2 D、4
二、填空题
-
11. 圆的半径为 , 圆的面积与半径之间有如下关系:.在这关系中,常量是.
-
12. 在函数中,自变量x的取值范围是 .
-
13. 已知二次函数 , 当时,函数的值是 .
-
14. 一次函数 的图象经过点 ,则 .
-
15. 已知函数y= ,若y=2,则x=.
-
16. 有边长为1的小等边三角形卡片若干张,使用这些三角形卡片拼出边长为2、3、4、……的大等边三角形(如图所示).
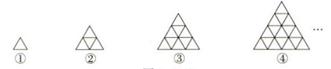
根据图形推断,每个大等边三角形所用的小等边三角形的卡片数S与大等边三角形的边长n的关系式是
三、解答题
-
17. 已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.
-
18. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h= gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?
-
19. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
 (1)、第一天中,骆驼体温的变化范围是从℃~℃,它的体温从最低到最高经过了小时.(2)、A点表示的是什么?图像中还有什么时间的温度与A点表示的温度相同?
(1)、第一天中,骆驼体温的变化范围是从℃~℃,它的体温从最低到最高经过了小时.(2)、A点表示的是什么?图像中还有什么时间的温度与A点表示的温度相同? -
20. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
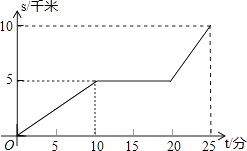 (1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
(1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少? -
21. 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
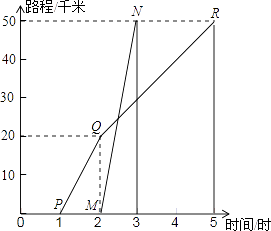 (1)、甲和乙哪一个出发的更早?早出发多长时间?(2)、甲和乙哪一个早到达B城?早多长时间?(3)、乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?(4)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?
(1)、甲和乙哪一个出发的更早?早出发多长时间?(2)、甲和乙哪一个早到达B城?早多长时间?(3)、乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?(4)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?
