重庆市开州区2021-2022学年九年级下学期期中数学试卷

试卷更新日期：2022-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $- 1$ ， $0$ ， $1$ ， $- 5 \frac{1}{3}$ 这四个数中，属于负整数的是（）

A、 $- 1$ B、 $0$ C、 $1$ D、 $- 5 \frac{1}{3}$

查看试题解析
2. 如图，该下列四个图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $5 b - 4 b = 1$ B、 $3 a \cdot 4 a b = 12 a^{2} b$ C、 ${(a^{2} b^{3})}^{2} = a^{4} b^{9}$ D、 ${(a - 2 b)}^{2} = a^{2} - 4 b^{2}$

查看试题解析
4. 估计 $2 \sqrt{2} \times \sqrt{6}$ 的运算结果应在下列哪两个数之间（）

A、5和6 B、6和7 C、7和8 D、8和9

查看试题解析
5. 下列命题，为真命题的是（）

A、三个角是直角的四边形是矩形 B、对角线相等的四边形是矩形 C、三条边相等的四边形是菱形 D、对角线互相垂直的四边形是菱形

查看试题解析
6. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这道题的意思是：今有若干人乘车，每三人共乘一车，最终剩余2辆车；若每2人共乘一车，最终剩余9个人无车可乘.问有多少人，多少辆车？设共有x人，y辆车，可列方程组为（）

A、 ${\begin{array}{l} 3 (y - 2) = x \\ x = 2 y - 9 \end{array}$ B、 ${\begin{array}{l} 3 (y + 2) = x \\ x = 2 y + 9 \end{array}$ C、 ${\begin{array}{l} 3 (y - 2) = x \\ x = 2 y + 9 \end{array}$ D、 ${\begin{array}{l} 3 (y + 2) = x \\ x = 2 y - 9 \end{array}$

查看试题解析
7. 如图，在平面直角坐标系中，△ABC与△A₁B₁C₁是位似图形.其中BC∶B₁C₁=1∶2，则△ABC与△A₁B₁C₁的周长之比是（）

A、1∶4 B、2∶1 C、1∶2 D、1∶3

查看试题解析
8. 如图，在 $⊙ O$ 中，AB为直径，CD为弦，若 $∠ A C D = 20 °$ ，则 $∠ B A D$ 的度数是（）

A、40° B、50° C、60° D、70°

查看试题解析
9. 如图，在正方形ABCD中，将边BC绕点B逆时针旋转至BC'，连接CC'，DC'，若∠CC'D = 90°，BC'= $2 \sqrt{5}$ ，则线段C'D的长度为（）

A、 $\sqrt{5}$ B、 $2$ C、 $4$ D、 $\frac{2 \sqrt{15}}{3}$

查看试题解析
10. A、B两地相距20 km，甲乙两人沿同一条路线从A地到B地，甲先出发，匀速行驶，甲出发1小时后乙再出发，乙以2 km/h的速度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达，甲、乙两人离开A地的距离S（km）与时间t（h）的关系如图所示，则下列选项错误的是（）

A、乙比甲先到1小时 B、甲的速度为4 km/h C、乙提速后速度为9 km/h D、乙出发两小时后追上甲

查看试题解析
11. 若a使关于x的不等式组 ${\begin{array}{l} \frac{x - 1}{2} < \frac{1 + x}{3} \\ 5 x - 2 \geq x + a \end{array}$ 有且只有四个整数解，且使关于y的方程 $\frac{y + a}{y - 1} + \frac{2 a}{1 - y} = 2$ 的解为非负数，则符合题意的所有整数α的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 定义：如果 $a^{x} = N$ （ $a > 0$ ，且 $a \neq 1$ ），那么x叫做以a为底N的对数，记做 $x = l o g_{a} N$ .例如：因为 $7^{2} = 49$ ，所以 $l o g_{7} 49 = 2$ ；因为 $5^{3} = 125$ ，所以 $l o g_{5} 125 = 3$ .下列说法：① $l o g_{6} 6 = 36$ ；② $l o g_{3} 81 = 4$ ；③若 $l o g_{4} (a + 14) = 2$ ，则 $a = 2$ ；④ $l o g_{2} 64 = l o g_{2} 32 + l o g_{2} 2$ ；正确的序号有（）

A、①③ B、②③ C、①②③ D、②③④

查看试题解析

二、填空题

13. 计算： $| 2 - \sqrt{5} | + {(- \frac{1}{2})}^{0} =$ .

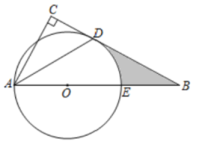
查看试题解析
14. 四个完全相同的球上分别标有数字 $- 1$ ， $- 4$ ， $0$ ， $5$ ，从这四个球中任意取出一个球记为a，放回后，再取出一个记为b，则点 $a + b$ 能被5整除的概率为.

查看试题解析
15. 如图，在△ABC中，∠C = 90°，点D在边BC上，以OA为半径的 $⊙ O$ 经过点D，连接AD，且AD平分∠BAC，若∠BAC = 60°， $⊙ O$ 的半径为2，则阴影部分的面积为 .

查看试题解析
16. 在新冠肺炎疫情发生后，某企业引进12条A、B、C型生产线生产防护服，A、B、C型生产线每条生产线每分钟的产量之比为4∶2∶1，为了扩大生产，该企业准备增加7条生产线，其中B型生产线增加1条，每条生产线（包括之前的和新增的生产线）每分钟的产量将增加4件.统计发现，增加生产线后，该企业每分钟的总产量恰比增加生产线前多142件，且A型生产线每分钟的产量与三种类型生产线每分钟的总产量之比为2∶5.请问，增加生产线后，该企业A、C型生产线每分钟的产量之比为 .

查看试题解析

三、解答题

17. 计算

(1)、 $(x - 2 y) (x + 2 y) - x (x - y)$ ；

(2)、 $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1}$ .

查看试题解析

18. 为培养学生良好的运动习惯和运动能力，我校本学期开展了“趣味运动会”和“冬季长跑”等体育活动.为了解九年级学生的长跑水平，我校对全体九年级同学进行了长跑测试，体育组陈老师随机抽取20名男生和20名女生的测试成绩（满分100）进行整理和分析（成绩共分成五组：A.

50 \leq x < 60

， B.

60 \leq x < 70

， C.

70 \leq x < 80

， D.

80 \leq x < 90

， E.

90 \leq x < 100

），绘制了不完整的统计图表：
（1）收集、整理数据

20名男生的长跑成绩分别为：

76，77，95，88，50，89，89，97，99，93，97，89，65，87，68，89，78，88，98，88.

女生长跑成绩在C组和D组的分别为：

73，74，74.74，74，76，83.88.89.

（2）分析数据：两组样本数据的平均数、中位数和众数如表所示：

长跑成绩	平均数	中位数	众数
男生	85	88.5	b
女生	81.8	a	74

请根据以上信息，回答下列问题；

(1)、①补全频数分布直方图；

②填空： $a =$ ▲ ， $b =$ ▲ ；

(2)、根据以上数据，你认为九年级学生是男生的长跑的成绩更好还是女生的长跑成绩更好？判断并说明理由（一条理由即可）；

(3)、如果我校九年级有男生900名，女生600名，请估计九年级长跑成绩不低于80分的学生人数.

查看试题解析

19. 一次函数 $y_{1} = k_{1} x + b (k_{1} \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象相交于点 $A (2 ， - 1)$ ， $B (1 ， n)$ 两点.

(1)、分别求出一次函数和反比例函数的解析式，并在给出的平面直角坐标系中，直接画出一次函数和反比例函数的图象；

(2)、连接AO并延长交双曲线于点C，连接BC，求△ABC的面积；

(3)、直接写出当 $y_{1} > y_{2}$ 时，x的取值范围.

查看试题解析
20. 如图，建筑物 $A B$ 后有一座小山， $∠ D C F = 30 °$ ，测得小山坡脚C点与建筑物水平距离 $B C = 25$ 米，若山坡上E点处有一凉亭，且凉亭与坡脚距离 $C E = 20$ 米，某人从建筑物顶端A点测得E点处的俯角为 $48 °$ .

(1)、求凉亭到地面的距离；

(2)、求建筑物 $A B$ 的高.（精确到 $0.1 m$ ）
（参考数据： $\sqrt{3} \approx 1.73$ ， $s i n 48 ° \approx 0.74$ ， $c o s 48 ° \approx 0.67$ ， $t a n 48 ° \approx 1.11$ ， $s i n 42 ° \approx 0.67$ ， $c o s 42 ° \approx 0.74$ ， $t a n 42 ° \approx 0.90$ ）

查看试题解析
21. 冰墩墩和雪容融是北京奥运会和冬残奥会吉祥物，冰墩墩是一只熊猫，它的外表给人一种朴实的感觉，雪容融是一个灯笼，它的外表总能给人温暖.钥匙扣，手办两用冰墩墩和雪容融立体挂件在奥林匹克官方旗舰店销售异常火爆.

(1)、开售第一天，旗舰店共花费84000元从授权生产厂家购进两种挂件各1000件，其中1件雪容融挂件成本比1件冰墩墩挂件成本少6元，则1件雪容融挂件成本和1件冰墩墩挂件成本分别是多少元？

(2)、开售第一天，冰墩墩和雪容融挂件很快售罄，售价分别为65元和55元.第二天，旗舰店又以第一天的成本价从授权生产厂家购进一批两种挂件，其中冰墩墩挂件售价提高了0.05a元，销售比第一天减少了2a件，而雪容融挂件售价不变，销量比第一天增加了0.125a件，最终旗舰店第二天销售两种挂件共获利36000元，求a的值.

查看试题解析
22. 若一个四位正整数m满足前两个数字组成的两位数是后两个数字组成的两位数的2倍，则把这个四位数m称为“Double数”.
例如：2010的前两个数字组成的两位数是：20，后两个数字组成的两位数是：10，
∵ $20 = 2 \times 10$ ， ∴2010是“Double数”；
9246的前两个数字组成的两位数是：92，后两个数字组成的两位数是：46，
∵ $92 = 2 \times 46$ ， ∴9246是“Double数”；
7525的前两个数字组成的两位数是：75，后两个数字组成的两位数是：25，
∵ $75 \neq 2 \times 25$ ， ∴7525不是“Double数”.

(1)、判断7035，3814是否是“Double数”？并说明理由；

(2)、记一个“Double数”m各个数位数字之和为 $D (m)$ ，令 $G (m) = \frac{m - D (m)}{9}$ .当 $G (m)$ 能被8整除时，求出所有符合条件的“Double数”m.

查看试题解析
23. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ ， $B (\frac{5}{2} ， 0)$ ，直线 $y = x + \frac{1}{2}$ 与抛物线交于C、D两点，与坐标轴交于E、F两点. 点P是抛物线在第四象限内图象上的一个动点.过点P作PG⊥CD，垂足为G，PQ∥y轴，交x轴于点Q.

(1)、求抛物线的解析式；

(2)、当 $\sqrt{2} P G + P Q$ 取得最大值时，求点P的坐标和 $\sqrt{2} P G + P Q$ 的最大值；

(3)、将抛物线向右平移 $\frac{13}{4}$ 个单位得到新抛物线，M为新抛物线对称轴上的一点，点N是平面内一点.当（2）中 $\sqrt{2} P G + P Q$ 最大时，直接写出所有使得以点A，P，M，N为顶点的四边形是菱形的点N的坐标.

查看试题解析
24. 在△ABC中，AB = AC，∠ABC = 30°，△BDE是等边三角形，连接CD、AE.

(1)、如图1，当A、B、D三点在同一直线上时，AE、BC交于点P，且AE⊥AC.若PC = 4，求PE的长；

(2)、如图2，当B、E、C三点在同一直线上时，F是CD中点，连接AF、EF，求证：AE = 2AF ；

(3)、如图3，在（2）的条件下，AB=8，E在直线BC上运动，将△AEF沿EF翻折得到△MEF，连接DM，G是AB上一点，且BG= $\frac{1}{4}$ AB，O是直线BC上的另一个动点，连接OG，将△BOG沿OG翻折得到△HOG，连接HM，当HM最小时，直接写出此时点D到直线EM的距离.

查看试题解析