江苏省淮安市洪泽区2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-04-25 类型:期中考试
一、单选题
-
1. 习近平主席在2022年新年贺词中提到“人不负青山,青山定不负人”,一语道出“人与自然和谐共生”的至简大道.下列有关环保的四个图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,最适合采用抽样调查的是( )A、调查一批防疫口罩的质量 B、调查某校初一一班同学的视力 C、为保证某种新研发的大型客机试飞成功,对其零部件进行检查 D、对乘坐某班次飞机的乘客进行安检3. 今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )A、2000名学生是总体 B、每位学生的数学成绩是个体 C、这100名学生是总体的一个样本 D、100名学生是样本容量4. 在 , , , , 中,分式的个数是( )A、2 B、3 C、4 D、55. 甲、乙两地相距m千米,某人从甲地前往乙地,原计划n小时到达,因故延迟了1小时到达,则他平均每小时比原计划少走的千米数为( )A、 B、 C、 D、6. 下列分式的变形正确的是( )A、=﹣ B、=x+y C、 D、7. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直8. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )
2. 下列调查中,最适合采用抽样调查的是( )A、调查一批防疫口罩的质量 B、调查某校初一一班同学的视力 C、为保证某种新研发的大型客机试飞成功,对其零部件进行检查 D、对乘坐某班次飞机的乘客进行安检3. 今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )A、2000名学生是总体 B、每位学生的数学成绩是个体 C、这100名学生是总体的一个样本 D、100名学生是样本容量4. 在 , , , , 中,分式的个数是( )A、2 B、3 C、4 D、55. 甲、乙两地相距m千米,某人从甲地前往乙地,原计划n小时到达,因故延迟了1小时到达,则他平均每小时比原计划少走的千米数为( )A、 B、 C、 D、6. 下列分式的变形正确的是( )A、=﹣ B、=x+y C、 D、7. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直8. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则AM的最小值是( )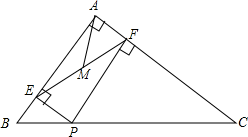 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 要反映无锡一周内每天的最高气温的变化情况,宜采用统计图.10. 若分式的值为0,则的值为 .11. 分式 , , 的最简公分母是.12. 某毛绒玩具厂对一批毛绒玩具进行质量抽检,相关数据如下:
抽取的毛绒玩具数
20
50
100
200
500
1000
1500
2000
优等品的频数
19
47
91
184
462
921
1379
1846
优等品的频率
0.950
0.940
0.910
0.920
0.924
0.921
0.919
0.923
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是.(精确到
13. 王老师为了解本班学生对新冠病毒防疫知识的掌握情况,对本班45名学生的新冠病毒防疫知识进行了测试,并把测试成绩分为5组,第1~4组的频数分别为12,10,6,8,则第5组的频率是 .14. 给出下列分式:
(1) , (2) , (3) , (4) , (5) 其中最简分式有.(填序号)15. 如图, 中, ,在同一平面内,将 绕点 旋转到 的位置,使得 ,则 等于. 16. 如图,△ABC的周长为19, 点D、E在边BC上,∠ABC的平分线垂直于AE,垂足为N ,∠ACB的平分线重直于AD,垂足为M,若BC=7,则MN的长度为.
16. 如图,△ABC的周长为19, 点D、E在边BC上,∠ABC的平分线垂直于AE,垂足为N ,∠ACB的平分线重直于AD,垂足为M,若BC=7,则MN的长度为.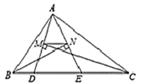
三、解答题
-
17. 约分(1)、(2)、18. 计算(1)、(2)、19. 先化简再求下列代数式的值:.20. 已知点E、F分别为平行四边形ABCD的边AD、BC的中点,求证:四边形EBFD为平行四边形.
 21. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,1),B(-1,3),C(-1,1).
21. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,1),B(-1,3),C(-1,1). (1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的 , 点的坐标为 ;(2)、平移△ABC,若点A对应的点的坐标为 , 画出 , 点的坐标为 ;(3)、当 , 绕某一点旋转可以得到(2)中的 , 直接写出旋转中心的坐标:.22. 在一只不透明的袋子中装有黑球、白球共10个,这些球除颜色外都相同,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过2000次重复摸球实验后,共摸出黑球1202次.(1)、估计袋中有黑球个;(2)、小明从袋中取出n个黑球后,小明从袋中剩余的球中随机摸出一个球是黑球的概率为 , 求n的值.23. 如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.
(1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的 , 点的坐标为 ;(2)、平移△ABC,若点A对应的点的坐标为 , 画出 , 点的坐标为 ;(3)、当 , 绕某一点旋转可以得到(2)中的 , 直接写出旋转中心的坐标:.22. 在一只不透明的袋子中装有黑球、白球共10个,这些球除颜色外都相同,小明每次摇匀后随机从袋中摸出一个球,记录颜色后放回袋中,通过2000次重复摸球实验后,共摸出黑球1202次.(1)、估计袋中有黑球个;(2)、小明从袋中取出n个黑球后,小明从袋中剩余的球中随机摸出一个球是黑球的概率为 , 求n的值.23. 如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF. (1)、求证:平行四边形ABCD是菱形;(2)、若DB=10,AB=13,求平行四边形ABCD的面积.24. 为了了解某校七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),其中,cm, cm,cm,D:165-170cm,cm,并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题:
(1)、求证:平行四边形ABCD是菱形;(2)、若DB=10,AB=13,求平行四边形ABCD的面积.24. 为了了解某校七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),其中,cm, cm,cm,D:165-170cm,cm,并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题: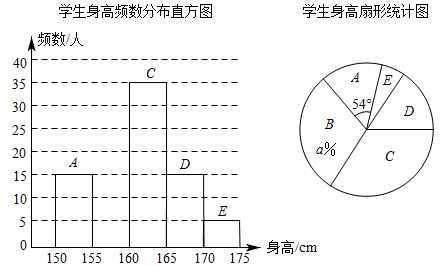 (1)、求抽取的样本容量是多少?(2)、B所占的百分比为 , 所在扇形的圆心角度数是 ;补全频数分布直方图;(3)、若该校七年级有名学生,估计该校七年级学生身高超过cm的学生有多少人?25. 如图,把矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)、求抽取的样本容量是多少?(2)、B所占的百分比为 , 所在扇形的圆心角度数是 ;补全频数分布直方图;(3)、若该校七年级有名学生,估计该校七年级学生身高超过cm的学生有多少人?25. 如图,把矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,使点E落在对角线BD上,连接DG,DF. (1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF=DC.26. 小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?
(1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF=DC.26. 小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?小红说:这个分式的分子、分母都含有x,它们的值均随x取值的变化而变化,有点难.
小刚说:我会解这类问题:当x取何整数时,分式的值是整数?3是x+1的整数倍即可,注意不要忘记负数哦.
小明说:可将分式与分数进行类比.本题可以类比小学里学过的“假分数”,当分子大于分母时,可以将“假分数”化为一个整数与“真分数”的和.比如:==2+(通常写成带分数:2).类比分式,当分子的次数大于或等于分母次数时,可称这样的分式为“假分式”,若将化成一个整式与一个“真分式”的和,就转化成小刚说的那类问题了!
小红、小刚说:对!我们试试看!…
(1)、解决小刚提出的问题;(2)、解决他们共同讨论的问题.27. 如图,在平行四边形中,的平分线交于点 , 交的延长线于F,以为邻边作平行四边形. (1)、证明平行四边形是菱形;(2)、若 , 连结 ,
(1)、证明平行四边形是菱形;(2)、若 , 连结 ,①求证:;
②求的度数;
(3)、若 , , , M是的中点,求的长.