浙江省温州市2022年中考数学备考模拟试卷
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、-6 B、-1 C、1 D、62. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:
班级
参加人数
平均数
中位数
方差
甲
55
135
149
191
乙
55
135
151
110
某同学分析上表后得出如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大.
上述结论中,正确的是( )
A、①② B、②③ C、①③ D、①②③3. 已知两个不等于0的实数 、 满足 ,则 等于( )A、-2 B、-1 C、1 D、24. 下列运算正确的是( )A、 B、 C、 D、5. 下列四个命题:①两直线平行,内错角相等;②对顶角相等;③等腰三角形的两个底角相等;④菱形的对角线互相垂直,其中逆命题是真命题的是( )A、①②③④ B、①③④ C、①③ D、①6. 红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )A、3种 B、4种 C、5种 D、6种7. 已知抛物线y=x2+2x+k+1与x轴有两个不同的交点,则一次函数y=kx﹣k与反比例函数y= 在同一坐标系内的大致图象是( )
A、 B、
B、 C、
C、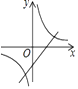 D、
D、 8. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( )
8. 如图,一束光线先后经平面镜 , 反射后,反射光线与平行,当时,的度数为( ) A、40° B、50° C、60° D、80°9. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、40° B、50° C、60° D、80°9. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )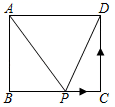 A、
A、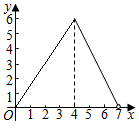 B、
B、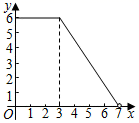 C、
C、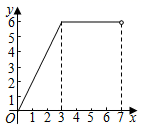 D、
D、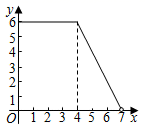 10. 若数a使关于x的不等式组 ,有且仅有三个整数解,且使关于y的分式方程 + =1有整数解,则满足条件的所有a的值之和是( )A、﹣10 B、﹣12 C、﹣16 D、﹣18
10. 若数a使关于x的不等式组 ,有且仅有三个整数解,且使关于y的分式方程 + =1有整数解,则满足条件的所有a的值之和是( )A、﹣10 B、﹣12 C、﹣16 D、﹣18二、填空题
-
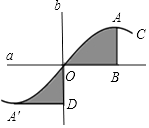
11. 计算: =12. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .
 13. 如图,AB是⊙O的切线,点B为切点,若∠A=30°,则∠AOB=.
13. 如图,AB是⊙O的切线,点B为切点,若∠A=30°,则∠AOB=. 14. 一副三角板如图所示摆放,且 ,则 的度数为 .
14. 一副三角板如图所示摆放,且 ,则 的度数为 .
 15. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm.
15. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 , 椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm. (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).16. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为cm(结果精确到0.1cm).16. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
三、解答题
-
17.(1)、计算(2)、先化简,再求值: , 其中 ,18.
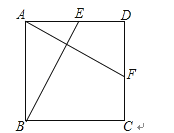
如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
 19. 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题
19. 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题组别
学习时间x(h)
频数(人数)
A
0<x≤1
8
B
1<x≤2
24
C
2<x≤3
32
D
3<x≤4
n
E
4小时以上
4
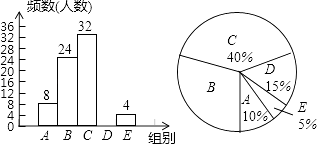 (1)、表中的n= , 中位数落在组,扇形统计图中B组对应的圆心角为°;(2)、请补全频数分布直方图;(3)、该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.20. 2020年12月30日,中共湘潭市委创造性地提出了深化“六个湘潭”(实力湘潭、创新湘潭、文化湘潭、幸福湘潭、美丽湘潭、平安湘潭)建设的发展目标.为响应政府号召,湘潭县湘莲种植户借助电商平台,在线下批发的基础上同步在电商平台“拼多多”上零售湘莲.已知线上零售、线下批发湘莲共获得4000元;线上零售和线下批发湘莲销售额相同.(1)、求线上零售和线下批发湘莲的单价分别为每千克多少元?(2)、该产地某种植大户某月线上零售和线下批发共销售湘莲 , 设线上零售 , 获得的总销售额为y元;
(1)、表中的n= , 中位数落在组,扇形统计图中B组对应的圆心角为°;(2)、请补全频数分布直方图;(3)、该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.20. 2020年12月30日,中共湘潭市委创造性地提出了深化“六个湘潭”(实力湘潭、创新湘潭、文化湘潭、幸福湘潭、美丽湘潭、平安湘潭)建设的发展目标.为响应政府号召,湘潭县湘莲种植户借助电商平台,在线下批发的基础上同步在电商平台“拼多多”上零售湘莲.已知线上零售、线下批发湘莲共获得4000元;线上零售和线下批发湘莲销售额相同.(1)、求线上零售和线下批发湘莲的单价分别为每千克多少元?(2)、该产地某种植大户某月线上零售和线下批发共销售湘莲 , 设线上零售 , 获得的总销售额为y元;①请写出y与x的函数关系式;
②若总销售额不低于70000元,则线上零售量至少应达到多少千克?
21. 如图,直线 与双曲线 相交于点A , 且 ,将直线向左平移一个单位后与双曲线相交于点B , 与x轴、y轴分别交于C、D两点.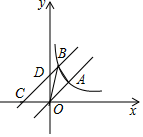 (1)、求直线 的解析式及k的值;(2)、连结 、 ,求 的面积.22. 如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)、求直线 的解析式及k的值;(2)、连结 、 ,求 的面积.22. 如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°. (1)、求证:CD是⊙O的切线,(2)、若⊙O的半径为3,求图中阴影部分的面积.23. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)、求证:CD是⊙O的切线,(2)、若⊙O的半径为3,求图中阴影部分的面积.23. 在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.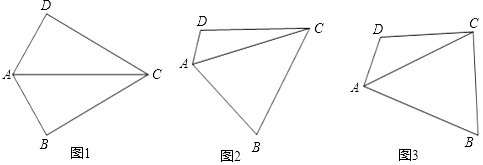 (1)、如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.(2)、如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)、如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.24. 已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(1)、如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.(2)、如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)、如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.24. 已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b. (1)、求抛物线顶点Q的坐标(用含a的代数式表示);(2)、说明直线与抛物线有两个交点;(3)、直线与抛物线的另一个交点记为N.
(1)、求抛物线顶点Q的坐标(用含a的代数式表示);(2)、说明直线与抛物线有两个交点;(3)、直线与抛物线的另一个交点记为N.(Ⅰ)若-1≤a≤ , 求线段MN长度的取值范围;
(Ⅱ)求△QMN面积的最小值.