浙江省绍兴市2022年中考模拟数学试卷
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 不考虑颜色,对如图的对称性表述,正确的是( )
 A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形2. 有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE , 如图②所示,则旋转角∠BAD的度数为( )
A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形2. 有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE , 如图②所示,则旋转角∠BAD的度数为( )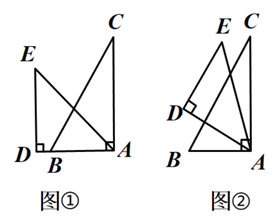 A、15° B、30° C、45° D、60°3. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、
A、15° B、30° C、45° D、60°3. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、 B、
B、 C、
C、 D、
D、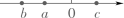 4. 反比例函数y= 的图象位于( )A、第一、三象限 B、第二、三象限 C、第一、二象限 D、第二、四象限5. 下列运算正确的是( )A、m2•m3=m6 B、m8÷m4=m2 C、3m+2n=5mn D、(m3)2=m66. 下列各数中,数值相等的是( )A、(﹣2)3和﹣23 B、﹣|23|和|﹣23| C、(﹣3)2和﹣32 D、23和327. 下列命题是真命题的是( )
4. 反比例函数y= 的图象位于( )A、第一、三象限 B、第二、三象限 C、第一、二象限 D、第二、四象限5. 下列运算正确的是( )A、m2•m3=m6 B、m8÷m4=m2 C、3m+2n=5mn D、(m3)2=m66. 下列各数中,数值相等的是( )A、(﹣2)3和﹣23 B、﹣|23|和|﹣23| C、(﹣3)2和﹣32 D、23和327. 下列命题是真命题的是( )
A、两直线平行,同位角相等 B、相似三角形的面积比等于相似比 C、菱形的对角线相等 D、相等的两个角是对顶角8. 如图, 是 的中线,四边形 是平行四边形,增加下列条件,能判断 是菱形的是( ) A、 B、 C、 D、9. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A、 B、 C、 D、9. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )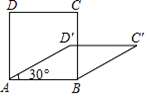 A、1 B、 C、 D、10. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )
A、1 B、 C、 D、10. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )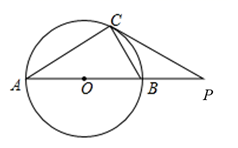 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
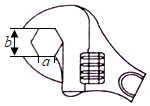
11. 因式分解:a2+ab﹣a= .12. 若 ,则x的取值范围是 .13. 文具店销售某种笔袋,每个18元,小华去购买这种笔袋,结账时店员说:“如果你再多买一个就可以打九折,价钱比现在便宜36元”,小华说:“那就多买一个吧,谢谢,”根据两人的对话可知,小华结账时实际付款元.14. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为mm.
 15. 矩形纸片 ,长 ,宽 ,折叠纸片,使折痕经过点B,交 边于点E,点A落在点 处,展平后得到折痕 ,同时得到线段 , ,不再添加其它线段,当图中存在 角时, 的长为厘米.
15. 矩形纸片 ,长 ,宽 ,折叠纸片,使折痕经过点B,交 边于点E,点A落在点 处,展平后得到折痕 ,同时得到线段 , ,不再添加其它线段,当图中存在 角时, 的长为厘米.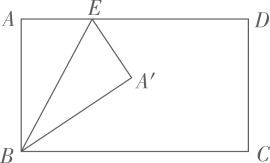 16. 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
16. 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .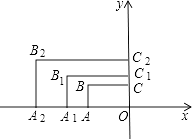
三、解答题
-
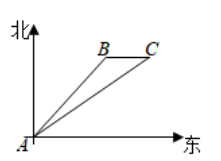
17.(1)、计算: ;(2)、化简: .18. 某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)19. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.
 20. 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
20. 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.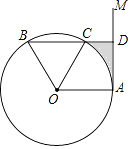 (1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).21. 已知平行四边形ABCD.
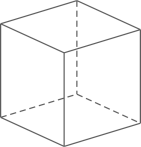
(1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).21. 已知平行四边形ABCD.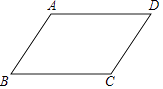 (1)、尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:CE=CF.22. 欧拉(Euler , 1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.(1)、观察下列多面体,并把下表补充完整:
(1)、尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:CE=CF.22. 欧拉(Euler , 1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.(1)、观察下列多面体,并把下表补充完整:名称
三棱锥
三棱柱
正方体
正八面体
图形
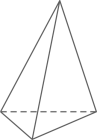
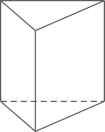

顶点数V
4
6
8
棱数E
6
12
面数F
4
5
8
(2)、分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式: .23. 如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B( ,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为 ,四边形BDEF为平行四边形.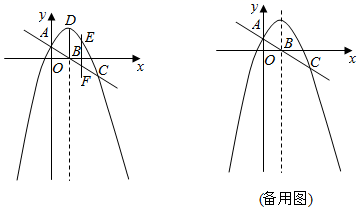 (1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.24. 在△ABC中,∠ABC=90°, =n , M是BC上一点,连接AM .
(1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.24. 在△ABC中,∠ABC=90°, =n , M是BC上一点,连接AM .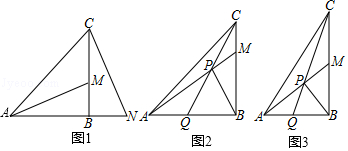 (1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN .(2)、过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q .
(1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN .(2)、过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q .①如图2,若n=1,求证: = .
②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示)