浙江省衢州市2022年中考数学模拟试卷三
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 小亮用天平称得一个罐头的质量为 ,用四舍五入法将 精确到 的近似值为( )A、 B、 C、 D、2. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 3. 喜迎建党100周年,某校将举办小合唱比赛,七个参赛小组人数如下:5,5,6,7,x , 7,8.已知这组数平均数是6,则这组数据的中位数( )A、5 B、5.5 C、6 D、74. 如图所示,该几何体的左视图是( )
3. 喜迎建党100周年,某校将举办小合唱比赛,七个参赛小组人数如下:5,5,6,7,x , 7,8.已知这组数平均数是6,则这组数据的中位数( )A、5 B、5.5 C、6 D、74. 如图所示,该几何体的左视图是( ) A、
A、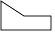 B、
B、 C、
C、 D、
D、 5. 如图,直线 被直线 所截下列条件能判定 的是( )
5. 如图,直线 被直线 所截下列条件能判定 的是( )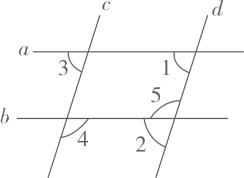 A、 B、 C、 D、6. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、7. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:
A、 B、 C、 D、6. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、7. 已知: 的顶点 ,点C在x轴的正半轴上,按以下步骤作图:①以点O为圆心,适当长为半径画弧,分别交 于点M , 交 于点N . ②分别以点M , N为圆心,大于 的长为半径画弧,两弧在 内相交于点E . ③画射线 ,交 于点 ,则点A的坐标为( )
 A、 B、 C、 D、8. 按一定规律排列的单项式:a, , , , , ,…,第n个单项式是( )A、 B、 C、 D、9. 若数a使关于x的不等式组 有且仅有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、﹣3 B、﹣2 C、﹣1 D、110. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B—C—A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
A、 B、 C、 D、8. 按一定规律排列的单项式:a, , , , , ,…,第n个单项式是( )A、 B、 C、 D、9. 若数a使关于x的不等式组 有且仅有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、﹣3 B、﹣2 C、﹣1 D、110. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B—C—A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( ) A、
A、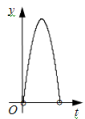 B、
B、 C、
C、 D、
D、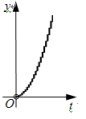
二、填空题
-
11. 计算:﹣(﹣2)=.12. 一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为元.13. 阅读材料:设 =(x1 , y1), =(x2 , y2),如果 ∥ ,则x1•y2=x2•y1 , 根据该材料填空,已知 =(4,3), =(8,m),且 ∥ ,则m=.14. 甲乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳次数的统计结果如表:
班级
参加人数
中位数
方差
平均数
甲
45
109
181
110
乙
45
111
108
110
某同学分析如表后得到如下结论:①甲,乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110次为优秀);③甲班成绩的波动比乙班大,则正确结论的序号是 .
15. 用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形 .图中, 度.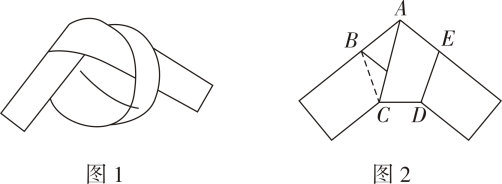 16. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕点A顺时针旋转到四边形 处,此时边 与对角线AC重叠,则图中阴影部分的面积是.
16. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕点A顺时针旋转到四边形 处,此时边 与对角线AC重叠,则图中阴影部分的面积是.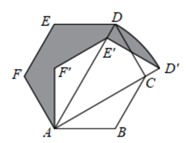
三、解答题
-
17. 解方程(组)(1)、(2)、18. 某市为了将生活垃圾合理分类,并更好地回收利用,将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 吨垃圾,将调查结果制成如下两幅不完整的统计图:
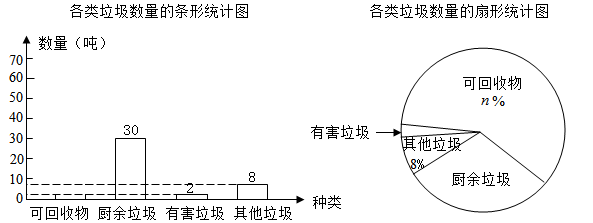
根据统计图提供的信息,解答下列问题:
(1)、 , ;(2)、根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中,厨余垃圾所对应的扇形圆心角的度数为度;(4)、根据抽样调查的结果,请你估计该市200吨垃圾中约有多少吨可回收物.19. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?20. 如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.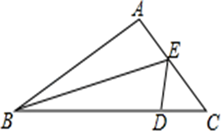 (1)、求证:△ABE≌△DBE;(2)、若∠A=100°,∠C=50°,求∠AEB的度数.21. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.
(1)、求证:△ABE≌△DBE;(2)、若∠A=100°,∠C=50°,求∠AEB的度数.21. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.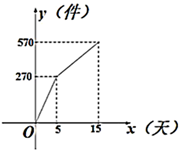 (1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)22. 如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.
(1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)22. 如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.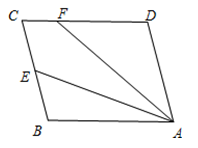 (1)、若∠D=105°,∠DAF=35°.求∠FAE的度数;(2)、求证:AF=CD+CF.23. 在平面直角坐标系中,抛物线与轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)、求点B的坐标(用含的式子表示);(2)、求抛物线的对称轴;(3)、已知点 , .若抛物线与线段PQ恰有一个公共点,结合函数图象,求的取值范围.24.
(1)、若∠D=105°,∠DAF=35°.求∠FAE的度数;(2)、求证:AF=CD+CF.23. 在平面直角坐标系中,抛物线与轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)、求点B的坐标(用含的式子表示);(2)、求抛物线的对称轴;(3)、已知点 , .若抛物线与线段PQ恰有一个公共点,结合函数图象,求的取值范围.24.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
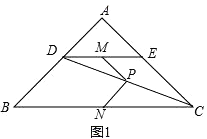 (1)、观察猜想
(1)、观察猜想图1中,线段PM与PN的数量关系是 , 位置关系是;
(2)、探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
 (3)、拓展延伸
(3)、拓展延伸把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.