浙江省衢州市2022年中考数学模拟试卷二
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 为贯彻落实觉中央、国务院关于推进城乡义务教育一体化发展的部署,教育部会同有关部门近五年来共新建、改扩建校舍186000000平方米,其中数据186000000用科学记数法表示是( )
A、1.86×107 B、186×106 C、1.86×108 D、0.186×1092. 某服装进货价80元/件,标价为200元/件,商店将此服装打x折销售后仍获利50%,则x为( )A、5 B、6 C、7 D、83. 下列立体图形中,主视图是矩形的是( )A、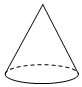 B、
B、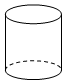 C、
C、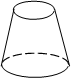 D、
D、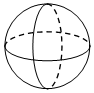 4. 已知函数 , 则自变量的取值范围是( )A、 B、﹣1且 C、 D、5. 若实数3是不等式2x–a–2<0的一个解,则a可取的最小正整数为( )A、2 B、3 C、4 D、56. 《你好,李焕英》的票房数据是:109,133,120,118,124,那么这组数据的中位数是( )A、124 B、120 C、118 D、1097. 如图,一把梯子靠在垂直水平地面的墙上,梯子 的长是3米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离BC为( )
4. 已知函数 , 则自变量的取值范围是( )A、 B、﹣1且 C、 D、5. 若实数3是不等式2x–a–2<0的一个解,则a可取的最小正整数为( )A、2 B、3 C、4 D、56. 《你好,李焕英》的票房数据是:109,133,120,118,124,那么这组数据的中位数是( )A、124 B、120 C、118 D、1097. 如图,一把梯子靠在垂直水平地面的墙上,梯子 的长是3米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离BC为( )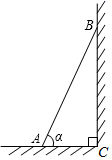 A、 米 B、 米 C、 米 D、 米8. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 已知 为实数﹐规定运算: , , , ,……, .按上述方法计算:当 时, 的值等于( )A、 B、 C、 D、10. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )A、2+ B、 C、2+或2- D、4+2或2-
A、 米 B、 米 C、 米 D、 米8. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 已知 为实数﹐规定运算: , , , ,……, .按上述方法计算:当 时, 的值等于( )A、 B、 C、 D、10. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )A、2+ B、 C、2+或2- D、4+2或2-二、填空题
-
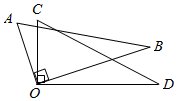
11. 2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数……现已知 ,则使用两次“调日法”可得到 的近似分数为.12. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
 13. 如图,在中, , 将平移5个单位长度得到 , 点、分别是、的中点,的最小值等于.
13. 如图,在中, , 将平移5个单位长度得到 , 点、分别是、的中点,的最小值等于.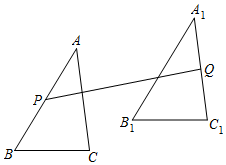 14. 一元二次方程 的解是 .15. 计算: .16. 某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款 元.
14. 一元二次方程 的解是 .15. 计算: .16. 某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款 元.三、解答题
-
17. 先化简,再求值:x(x+1)+(2+x)(2﹣x),其中x= ﹣4.18. 在的方格纸中,的三个顶点都在格点上.
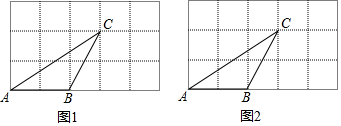 (1)、在图1中画出线段BD,使 , 其中D是格点;(2)、在图2中画出线段BE,使 , 其中E是格点.19. 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)的百分比的统计图,如图所示,根据统计图回答下列问题:
(1)、在图1中画出线段BD,使 , 其中D是格点;(2)、在图2中画出线段BE,使 , 其中E是格点.19. 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)的百分比的统计图,如图所示,根据统计图回答下列问题: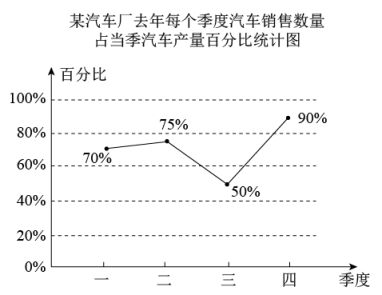 (1)、若第一季度的汽车销售数量为2100辆,求该季度的汽车产量;(2)、圆圆同学说:“因为第二、第三这两个季度汽车占当季汽车产量的百分比由75%降为50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说得对吗?为什么?20. 已知变量x、y对应关系如下表已知值呈现的对应规律.
(1)、若第一季度的汽车销售数量为2100辆,求该季度的汽车产量;(2)、圆圆同学说:“因为第二、第三这两个季度汽车占当季汽车产量的百分比由75%降为50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说得对吗?为什么?20. 已知变量x、y对应关系如下表已知值呈现的对应规律.x
…
﹣4
﹣3
﹣2
﹣1
1
2
3
4
…
y
…
1
2
﹣2
﹣1
﹣
﹣
…
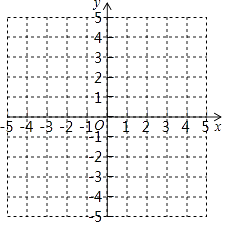 (1)、依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(1)、依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)、在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于 ,求出P点坐标.21. 为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.(1)、今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)、试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
22. 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.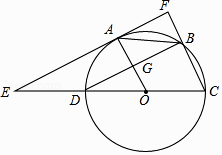 (1)、求证:EF是⊙O的切线;(2)、求AE的长.23. 如图1,在等腰三角形 中, 点 分别在边 上, 连接 点 分别为 的中点.
(1)、求证:EF是⊙O的切线;(2)、求AE的长.23. 如图1,在等腰三角形 中, 点 分别在边 上, 连接 点 分别为 的中点.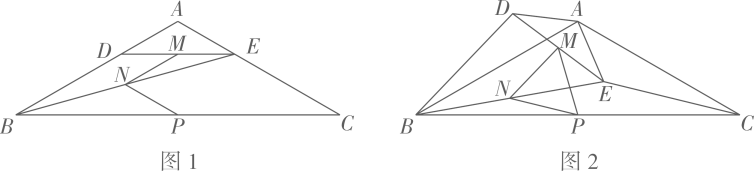 (1)、观察猜想
(1)、观察猜想图1中,线段 的数量关系是 , 的大小为;
(2)、探究证明把 绕点A顺时针方向旋转到如图2所示的位置,连接 判断 的形状,并说明理由;
(3)、拓展延伸把 绕点A在平面内自由旋转,若 ,请求出 面积的最大值.
24. 如图,直线y=﹣2x+4交y轴于点A,交抛物线y= x2+bx+c于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.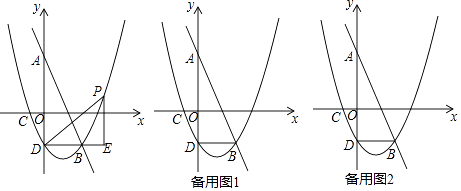 (1)、求抛物线的解析式;(2)、当△PDE为等腰直角三角形时,求出PE的长及P点坐标;(3)、在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.
(1)、求抛物线的解析式;(2)、当△PDE为等腰直角三角形时,求出PE的长及P点坐标;(3)、在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.