浙江省宁波市镇海区2022年九年级学业考试一模数学试卷
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
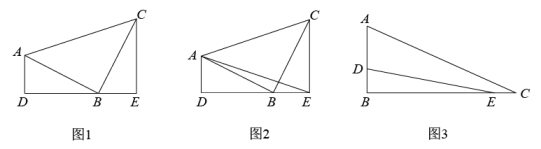
1. 下列四个数中,最大的数是( )A、﹣2 B、 C、0 D、62. 计算:的结果是( )A、 B、 C、 D、3. 若一个三角形的两边长分别为5和8,则第三边长可能是( )A、14 B、10 C、3 D、24. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、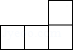 B、
B、 C、
C、 D、
D、 5. 如图是自动测量仪记录的图象,它反映了某市的春季某天气温如何随时间的变化而变化.下列从图象中得到的信息正确的是( )
5. 如图是自动测量仪记录的图象,它反映了某市的春季某天气温如何随时间的变化而变化.下列从图象中得到的信息正确的是( ) A、0点时气温达到最低 B、最低气温是零下4℃ C、0点到14点之间气温持续上升 D、最高气温是8℃6. 一个不透明布袋里装有1个白球、2个黑球、3个红球,它们除颜色外均相同,从中任意摸出一个球,则是红球的可能性为( )A、 B、 C、 D、7. 关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k的值为( )A、k=4 B、k=﹣4 C、k≥﹣4 D、k≥48. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,反比例函数图象的表达式为(),图象与图象关于直线对称,直线与交于 , 两点,当为中点时,则的值为( )
A、0点时气温达到最低 B、最低气温是零下4℃ C、0点到14点之间气温持续上升 D、最高气温是8℃6. 一个不透明布袋里装有1个白球、2个黑球、3个红球,它们除颜色外均相同,从中任意摸出一个球,则是红球的可能性为( )A、 B、 C、 D、7. 关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k的值为( )A、k=4 B、k=﹣4 C、k≥﹣4 D、k≥48. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、9. 如图,反比例函数图象的表达式为(),图象与图象关于直线对称,直线与交于 , 两点,当为中点时,则的值为( )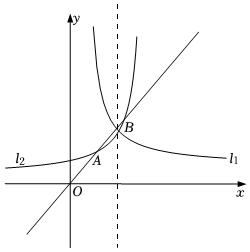 A、 B、 C、 D、10. 如图,在中, , , 将绕点顺时针旋转至 , 点刚好落在直线上,则的面积为( )
A、 B、 C、 D、10. 如图,在中, , , 将绕点顺时针旋转至 , 点刚好落在直线上,则的面积为( )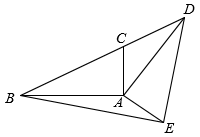 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 不等式的解是.12. 数据5,5,4,5,3,1的中位数是.13. 当 , 时,代数式的值是.14. 扇形的半径为3,弧长为2π,则扇形的面积为(结果保留).15. 如图,在四边形中, , , , 点在对角线上运动,为的外接圆,当与四边形的一边相切时,其半径为.
 16. 如图,在中, , 点为中点,点在边上, , 将沿折叠至 , 若 , 则.
16. 如图,在中, , 点为中点,点在边上, , 将沿折叠至 , 若 , 则.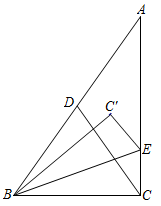
三、解答题
-
17.(1)、计算:;(2)、计算:.18. 某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本
学生人数
1
15
2
a
3
b
4
5
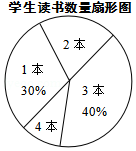 (1)、直接写出m、a、b的值;(2)、估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?19. 在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
(1)、直接写出m、a、b的值;(2)、估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?19. 在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).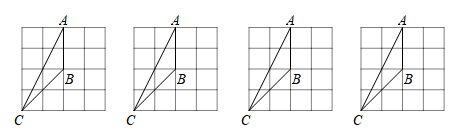 20. 图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.
20. 图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.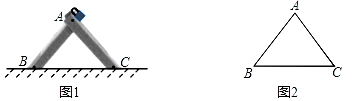
(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
(1)、求车位锁的底盒长BC.(2)、若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?21. 如图,在平面直角坐标系中,二次函数图象的顶点是A,与轴交于 , 两点,与轴交于点.点的坐标是.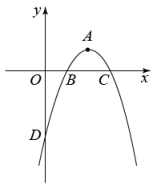 (1)、求A,两点的坐标,并根据图象直接写出当时的取值范围;(2)、将图象向上平移个单位后,二次函数图象与轴交于 , 两点,若 , 求的值.22. 要从甲、乙两仓库向 , 两工地运送水泥.已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;工地需70吨水泥,工地需110吨水泥.设甲运往地的水泥为()吨,两仓库到 , 两工地的运量和每吨的运费如下表:
(1)、求A,两点的坐标,并根据图象直接写出当时的取值范围;(2)、将图象向上平移个单位后,二次函数图象与轴交于 , 两点,若 , 求的值.22. 要从甲、乙两仓库向 , 两工地运送水泥.已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;工地需70吨水泥,工地需110吨水泥.设甲运往地的水泥为()吨,两仓库到 , 两工地的运量和每吨的运费如下表:运量
运费(元/吨)
甲仓库
乙仓库
甲仓库
乙仓库
地
____
24
18
地
____
____
25
16
(1)、根据题意,完成表格;(2)、求出总运费关于的函数表达式;(3)、利用一次函数的增减性,求出的最小值.