浙江省金华市婺城区2022年中考调研数学试卷

试卷更新日期：2022-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 在四个数 $- π$ ， 0，-3，10中，最大的数是（）

A、 $- π$ B、-3 C、0 D、10

查看试题解析
2. 下列四个几何体中，左视图为圆的是（）

A、 B、 C、 D、

查看试题解析
3. 金华轨道交通是服务于金华市的城市轨道交通系统，其首条线路——金义东线金义段已正式通行，线路全长约107000米. 用科学记数法表示数107000结果为（）

A、 $1.07 \times 1 0^{5}$ B、 $10.7 \times 1 0^{4}$ C、 $107 \times 1 0^{3}$ D、 $0.17 \times 1 0^{6}$

查看试题解析
4. 正数2的平方根可以表示为（）

A、 $2^{2}$ B、 $\pm \sqrt{2}$ C、 $\sqrt{2}$ D、 $- \sqrt{2}$

查看试题解析
5. 测试五位学生的“一分钟仰卧起坐”成绩，得到五个各不相同的数据. 在统计时，出现了一处错误：将最高成绩50个写成了55个.则下列统计量不受影响的是（）

A、方差 B、标准差 C、中位数 D、平均数

查看试题解析
6. 视力表用来测量一个人的视力.如图是视力表的一部分，其中开口向下的两个“E”之间的变换是（）

A、平移 B、旋转 C、轴对称 D、位似

查看试题解析
7. 七巧板是中国古代劳动人民的发明.小张为祝贺辛丑年的到来，用一副七巧板，拼成了“牛气冲天”的图案（如图）. 图中∠ABC与∠DEF的和为（）

A、180° B、225° C、270° D、360°

查看试题解析
8. 已知反比例函致 $y = - \frac{4}{x}$ ，下列说法中错误的是（）

A、图象经过点（1，﹣4） B、图象位于第二、四象限 C、图象关于直线y＝x对称 D、y随x的增大而增大

查看试题解析
9. 如图1，将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下，使木桩向上运动.如果楔子斜面的倾斜角为10°，楔子沿水平方向前进6厘米（如图2），那么木桩上升的高度为（）

A、 $6 s i n 10 °$ 厘米 B、 $6 c o s 10 °$ 厘米 C、 $6 t a n 10 °$ 厘米 D、 $\frac{6}{t a n 10 °}$ 厘米

查看试题解析
10. 如图，在平行四边形ABCD纸片中，∠BAD=45°，AB=10.将纸片折叠，使得点A的对应点A＇落在BC边上，折痕EF交AB、AD、AA＇分别于点E、F、G. 继续折叠纸片，使得点C的对应点C＇落在A＇F上.连接GC＇，则GC＇的最小值为（）

A、 $\frac{5}{2}$ B、 $\frac{5 \sqrt{2}}{2}$ C、 $\frac{5}{4}$ D、 $\frac{5 \sqrt{2}}{4}$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 2}$ 中，字母 $x$ 的取值范围是．

查看试题解析
12. 如图，现有四张卡片，前三张卡片上的数分别为3、6、7. 在第四张卡片上填写一个数，使得从中任取一张，取到奇数的概率与取到偶数的概率相等. 你填写的数是.（填写一个你认为正确的数即可）.

查看试题解析
13. 如果 $2 x - y = 1$ ，那么 $2 y - 4 x + 2024 =$ .

查看试题解析
14. 量角器的中心记为点O，测角度时摆放的位置如图所示，点A、B在以O为圆心的半圆上，OA、OB、OC分别与0°、140°、60°刻度线重合.射线OC交AB于点D，则∠ADC＝°.

查看试题解析
15. 如图，点D是等腰Rt△ABC的重心，其中∠ACB＝90°，将线段CD绕点C逆时针旋转90°得到线段CE，连结DE.若△ABC的周长为 $6 \sqrt{2}$ ，则△DCE的周长为.

查看试题解析
16. 已知圆柱形瓶子的底面半径为 $\frac{12}{π}$ cm.其侧面贴合了一条宽为3cm的环形装饰带.

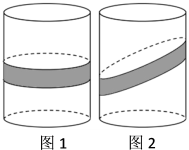(1)、如图1，若装饰带水平环绕，则瓶子侧面被装饰带覆盖的面积为cm²；

(2)、如图2，若装饰带斜贴侧面环绕，装饰带的最高点与最低点高度差为4cm，则瓶子侧面被装饰带覆盖的面积为cm².

查看试题解析

三、解答题

17. 计算： $（ 3 - π ）^{0} - 2 s i n 30 ° - \sqrt{12} + | 1 - 2 \sqrt{3} |$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} x - 3 \leq 0 \\ \frac{x - 2}{2} - 4 < 3 x \end{array}$ .

查看试题解析
19. 如图，雨伞不论张开还是收紧，伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时，点D与点M重合，且点A，E（F），D在同一条直线上.已知伞骨的部分长度如下（单位：cm）：DE=DF=AE=AF=40.

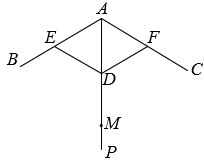(1)、求AM的长.

(2)、当伞撑开时，量得∠BAC=110°，求AD的长.（结果精确到1cm）
参考数据： $s i n 55 ° \approx 0.8192 ， c o s 55 ° \approx 0.5736 ， t a n 55 ° \approx 1.4281$ .

查看试题解析
20. 2021年秋季教育部明确提出，要减轻义务教育阶段学生的作业负担，学生的校外培训负担.依据政策要求，初中书面作业平均完成时间不超过90分钟，学生每天的完成作业时长不能超过2小时.某中学为了积极推进教育部的新政策实施，对本校学生的作业情况进行了抽样调查，统计结果如图所示：

(1)、这次抽样共调查了 ▲ 名学生，并补全条形统计图.

(2)、计算扇形统计图中表示作业时长为2.5小时对应的扇形圆心角度数.

(3)、若该中学共有学生3000人，请据此估计该校学生的作业时间不少于2小时的学生人数.

查看试题解析
21. 如图，⊙O的半径OC垂直于弦AB于点D，点P在OC的延长线上，AC平分∠PAB.

(1)、判断AP与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为4，弦AB平分OC，求 $\overset{⌢}{B C}$ 与弦AB、AC围成的阴影部分的面积.

查看试题解析
22. 跳台滑雪是北京冬奥会的比赛项目之一.下图是某跳台滑雪场地的截面示意图. 平台AB长1米（即AB=1），平台AB距地面18米.以地面所在直线为x轴，过点B垂直于地面的直线为y轴，取1米为单位长度，建立平面直角坐标系.已知滑道对应的函数为 $y = \frac{k}{x} (x \geq 1)$ .运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落过程中的某位置（忽略空气阻力）.设运动员飞出时间为t秒，运动员与点A的竖直距离为h米，运动员与点A的水平距离为l米.经实验表明：h=6t² ， l=vt.

(1)、求k的值；

(2)、当v=5，t=1时，通过计算判断运动员是否落在滑道上；

(3)、若运动员甲、乙同时从A处飞出，已知甲离开点A的速度是5米/秒.当甲距x轴4.5米时，乙恰好位于甲右侧4.5米的位置，求t的值与运动员乙离开A的速度.

查看试题解析
23. 定义：对于两个关于x的函数y₁ ， y₂.如果x=t，两个函数的函数值相等，即y₁=y₂ ，那么称y₁ ， y₂互为“等值函数”，其中x=t叫做函数y₁ ， y₂的“等值根”.例如：对于函数 $y_{1} = 2 x ， y_{2} = - x + 3$ .当x=1时，y₁=y₂=2.因此y₁ ， y₂互为“等值函数”，x=1是这两个函数的“等值根”.

(1)、函数 $y = x - 1$ 与 $y = \frac{1}{x}$ （填“是”或“不是”）“等值函数”；

(2)、已知函数 $y_{1} = k (x - 1) + 1$ 与 $y_{2} = {\begin{array}{l} 2 x - 2 (x \geq 1) \\ 2 - 2 x (x < 1) \end{array}$ ， $y_{3} = - | x^{2} + 2 x |$ .函数y₂的图象如图所示.
①若 $k = - 1$ ，求y₁与y₂的“等值根”；
②若y₁与y₂只存在一个“等值根”，则k的取值范围为 ▲ 。
③若函数y₁与y₃互为“等值函数”，且有两个“等值根”，请直接写出k的取值范围.

查看试题解析
24. 如图，在矩形ABCD中，AB=2，BC=4，点E在直线AB上，连结DE，过点A作AF⊥DE交直线BC于点F，以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H.

(1)、当点E在线段AB上时，求证：△ABF ∽△DAE.

(2)、当AE=2时，求EH的长.

(3)、在点E的运动过程中，是否存在某一位置，使得△EGH为等腰三角形.若存在，求AE的长.

查看试题解析