浙江省湖州市2022年中考模拟数学试卷
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 计算(ab2)3的结果是( )A、3ab2 B、ab6 C、a3b5 D、a3b63. 下列长度的三条线段,能组成三角形的是( )
A、4cm,5cm,9cm B、8cm,8cm,15cm C、5cm,5cm,10cm D、6cm,7cm,14cm4. 菱形的两条对角线长分别是6和8,则此菱形的周长是( )A、5 B、20 C、24 D、325. 不等式组 的解集为( )A、x≤2 B、x<4 C、2≤x<4 D、x≥26. 一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字是偶数的概率为( ).A、 B、 C、 D、7. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
A、1 B、﹣3 C、3 D、48. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、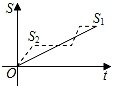 B、
B、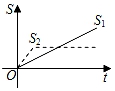 C、
C、 D、
D、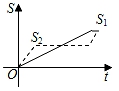 9. 欣欣服装店某天用相同的价格 卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )A、盈利 B、亏损 C、不盈不亏 D、与售价 有关10. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )
9. 欣欣服装店某天用相同的价格 卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )A、盈利 B、亏损 C、不盈不亏 D、与售价 有关10. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )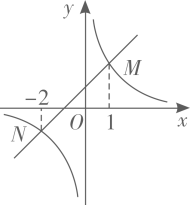 A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题
-
11. 分解因式: .12. 已知直线 ,将一块含 角的直角三角板ABC按如图所示方式放置( ),并且顶点A , C分别落在直线a , b上,若 ,则 的度数是 .
 13. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
13. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 . 14. 如图,一个正方体由 27 个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.
14. 如图,一个正方体由 27 个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块. 15. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为.
15. 如图①是山东舰航徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为12的圆锥侧面展开图(如图②),则该圆锥的母线长 为.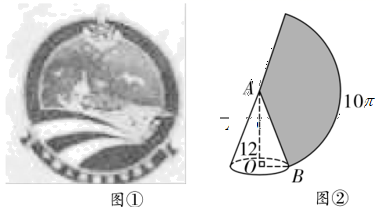 16. 如图,中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=度.
16. 如图,中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=度.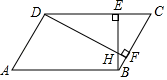
三、解答题
-
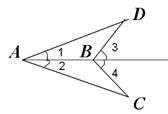
17. 已知:∠1=∠2,∠3=∠4.求证:AC=AD
 18.(1)、化简求值: ,其中 ;(2)、解方程 .19. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .
18.(1)、化简求值: ,其中 ;(2)、解方程 .19. 如图,“开心”农场准备用 的护栏围成一块靠墙的矩形花园,设矩形花园的长为 ,宽为 .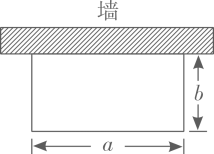 (1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.20. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)、当 时,求b的值;(2)、受场地条件的限制,a的取值范围为 ,求b的取值范围.20. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.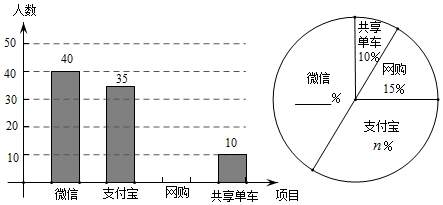 (1)、根据图中信息求出m= , n=;
(1)、根据图中信息求出m= , n=;
(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)、已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.21. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为 . (1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.22. 教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
(1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.22. 教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
请根据教材提示,结合图①,写出完整的证明过程.

结论应用:在 ▱ ABCD中,对角线AC、BD、交于点O,E为边BC的中点,AE、BD交于点F.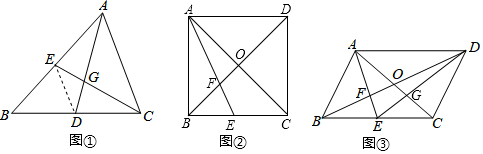 (1)、如图②,若为正方形,且 , 则的长为_.(2)、如图③,连结交于点 , 若四边形的面积为 , 则的面积为_.23. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .
(1)、如图②,若为正方形,且 , 则的长为_.(2)、如图③,连结交于点 , 若四边形的面积为 , 则的面积为_.23. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .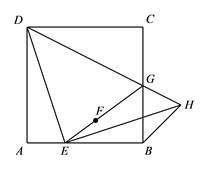 (1)、求证: ;
(1)、求证: ;
(2)、用等式表示线段 与 的数量关系,并证明.24. 如图,抛物线经过点B(3,0),C(0,-2),直线L:交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).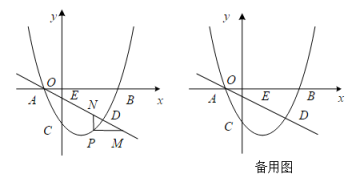 (1)、求抛物线的解析式.(2)、当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.(3)、设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
(1)、求抛物线的解析式.(2)、当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.(3)、设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.