浙江省杭州市2022年中考模拟数学试卷
试卷更新日期:2022-04-25 类型:中考模拟
一、单选题
-
1. 在实数 ,-3, , 中,最小的数是( )A、 B、-3 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图所示,四边形 是平行四边形,点 在线段 的延长线上,若 ,则 ( )
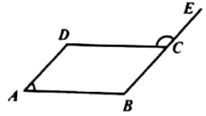 A、 B、 C、 D、4. 如图,在 中, , 平分 ,则 的度数为( )
A、 B、 C、 D、4. 如图,在 中, , 平分 ,则 的度数为( ) A、 B、 C、 D、5. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 上一点,BD交AC于点E,若BC=4,AD= ,则AE的长是( )
A、 B、 C、 D、5. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 上一点,BD交AC于点E,若BC=4,AD= ,则AE的长是( ) A、1 B、1.2 C、2 D、36. 已知x﹣y=4,xy=2,那么(x+y)2的值为( )A、24 B、20 C、12 D、87. 不等式 的解集在数轴上表示为( )A、
A、1 B、1.2 C、2 D、36. 已知x﹣y=4,xy=2,那么(x+y)2的值为( )A、24 B、20 C、12 D、87. 不等式 的解集在数轴上表示为( )A、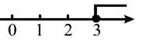 B、
B、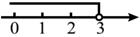 C、
C、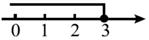 D、
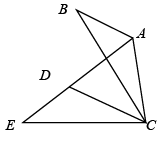
D、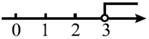 8. 关于x的分式方程 3=0有解,则实数m应满足的条件是( )A、m=﹣2 B、m≠﹣2 C、m=2 D、m≠29. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
8. 关于x的分式方程 3=0有解,则实数m应满足的条件是( )A、m=﹣2 B、m≠﹣2 C、m=2 D、m≠29. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
 A、 B、 C、 D、10. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )
A、 B、 C、 D、10. 如图,在 和 中, , , .连接CD , 连接BE并延长交AC , AD于点F , G . 若BE恰好平分 ,则下列结论错误的是( )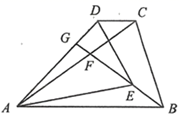 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若一组数据 的平均数为6,众数为5,则这组数据的方差为 .12. 已知圆锥形工件的底面直径是40cm,母线长30cm,其侧面展开图圆心角的度数为 .13. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.
 14. 如图,在 中, , ,分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则 .
14. 如图,在 中, , ,分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则 .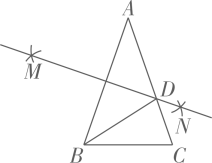 15. 已知 ,当分别取1,2,3,……,2020时,所对应y值的总和是.16. 如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为 , 折痕为DE.若将∠B沿向内翻折,点B恰好落在DE上,记为 , 则AB=.
15. 已知 ,当分别取1,2,3,……,2020时,所对应y值的总和是.16. 如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为 , 折痕为DE.若将∠B沿向内翻折,点B恰好落在DE上,记为 , 则AB=.
三、解答题
-
17.(1)、计算:(2)、先化简: ,然后 从0、1、2三个数中选一个你认为合适的数代入求值.18. 雾霾天气严重影响市民的生活质量.在今年寒假期间,某校八年一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察分析并回答下列问题.
组别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
C
炉烟气排放
15%
D
其他(滥砍滥伐等)
 (1)、本次被调查的市民共有多少人?(2)、分别补全条形统计图和扇形统计图,并计算图2中区域B所对应的扇形圆心角的度数.(3)、若该市有100万人口,请估计持有A.B两组主要成因的市民有多少人?19. 如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y= 的图象有唯一的公共点C.
(1)、本次被调查的市民共有多少人?(2)、分别补全条形统计图和扇形统计图,并计算图2中区域B所对应的扇形圆心角的度数.(3)、若该市有100万人口,请估计持有A.B两组主要成因的市民有多少人?19. 如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y= 的图象有唯一的公共点C.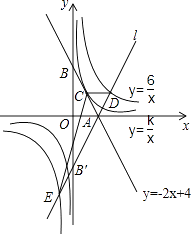 (1)、求k的值及C点坐标;(2)、直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y= 交于D、E两点,求△CDE的面积.20. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(2)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?(3)、超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
(1)、求k的值及C点坐标;(2)、直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y= 交于D、E两点,求△CDE的面积.20. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(2)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?(3)、超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?
21. 如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°. (1)、求证:BD是⊙O的切线,(2)、求图中阴影部分的面积.22. 【操作发现】
(1)、求证:BD是⊙O的切线,(2)、求图中阴影部分的面积.22. 【操作发现】在计算器上输入一个正数,不断地按“
 ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后再x轴上确定对应的数x2 , …,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
 (1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若 , b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;
(1)、若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;(2)、若k>1,又得到什么结论?请说明理由;(3)、①若 , b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
23. 已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.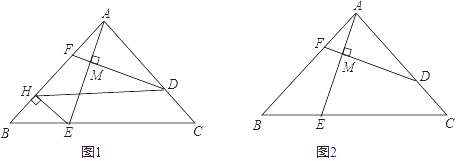 (1)、如图1,过点E作EH⊥AB于点H,连结DH.
(1)、如图1,过点E作EH⊥AB于点H,连结DH.①求证:四边形DHEC是平行四边形;
②若m= ,求证:AE=DF;
(2)、如图2,若m= ,求 的值.