广东省广州市八校联考2021-2022学年高一下学期数学期中（B卷）试卷

试卷更新日期：2022-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 若复数z满足 $z + 2 \bar{z} = 6 + 3 i$ ，则在复平面内复数z对应的点Z位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知向量 $\vec{a}$ =（k，1）， $\vec{b}$ =（3，2）， $\vec{c}$ =（1，3），且（ $\vec{a} - \vec{b}$ ） $⊥$ $\vec{c}$ ，则实数k的值等于（）

A、 $\frac{8}{3}$ B、 $\frac{10}{3}$ C、6 D、8

查看试题解析
3. 在△ABC中，角A，B，C的对边分别是a，b，c，已知 $a^{2} = b^{2} + c^{2} + b c$ ，则A=（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、 $\frac{3 π}{4}$ D、 $\frac{5 π}{6}$

查看试题解析
4. 不等式 $l o g_{2} (3 x + 1) < 1$ 成立的一个充分不必要条件是（）

A、 $- \frac{1}{3} < x < \frac{1}{3}$ B、 $x < 0$ C、 $- 1 < x < \frac{1}{3}$ D、 $0 < x < \frac{1}{3}$

查看试题解析
5. 在△ABC中，D为BC上一点，满足BD=2DC，则 $\vec{A D}$ 等于（）

A、 $\frac{1}{6} \vec{A B} + \frac{5}{6} \vec{A C}$ B、 $\frac{5}{6} \vec{A B} + \frac{1}{6} \vec{A C}$ C、 $\frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C}$ D、 $\frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C}$

查看试题解析
6. 已知单位向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} \cdot \vec{b}$ $= - \frac{1}{4}$ ，若向量 $\vec{c} = \vec{a} + 2 \vec{b}$ ，则 $c o s$ 〈 $\vec{a}$ ， $\vec{c}$ 〉=（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{2}}{3}$ C、 $\frac{1}{4}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
7. 函数 $f (x) = s i n (ω x - \frac{π}{2}) (ω > 0)$ 在 $[0 ， \frac{π}{5}]$ 上单调递增，则 $ω$ 的最大值为（）

A、6 B、5 C、4 D、1

查看试题解析
8. 在 $Δ A B C$ 中，点 $P$ 满足 $\overset{⇀}{B P} = 3 \overset{⇀}{P C}$ ，过点 $P$ 的直线与 $A B$ 、 $A C$ 所在的直线分别交于点 $M$ 、 $N$ ，若 $\overset{⇀}{A M} = λ \overset{⇀}{A B}$ ， $\overset{⇀}{A N} = μ \overset{⇀}{A C} (λ > 0 ， μ > 0)$ ，则 $λ + μ$ 的最小值为（）

A、 $\frac{\sqrt{2}}{2} + 1$ B、 $\frac{\sqrt{3}}{2} + 1$ C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析

二、多选题

9. 下列命题为真命题的是（）

A、若 $z_{1} ， z_{2}$ 互为共轭复数，则 $z_{1} z_{2}$ 为实数 B、若 $i$ 为虚数单位， $n$ 为正整数，则 $i^{4 n + 3} = i$ C、复数 $\frac{4 + a i}{1 + i}$ （ $i$ 为虚数单位， $a$ 为实数）为纯虚数，则 $a = - 4$ D、若 $m$ 为实数， $i$ 为虚数单位，则“ $\frac{2}{3} < m < 1$ ”是“复数 $m (3 + i) - (2 + i)$ 在复平面内对应的点位于第四象限”的充要条件

查看试题解析
10. 在 $△ A B C$ 中各角所对得边分别为a，b，c，下列结论正确的有（）

A、 $\frac{a}{c o s A} = \frac{b}{c o s B} = \frac{c}{c o s C}$ 则 $△ A B C$ 为等边三角形； B、已知 $(a + b + c) (a + b - c) = 3 a b$ ，则 $∠ C = 6 0^{∘}$ ； C、已知 $a = 7$ ， $b = 4 \sqrt{3}$ ， $c = \sqrt{13}$ ，则最小内角的度数为 $3 0^{∘}$ ； D、在 $a = 5$ ， $A = 6 0^{∘}$ ， $b = 4$ ，解三角形有两解．

查看试题解析
11. 中国南宋时期杰出数学家秦九韶在《数书九章》中提出了已知三角形三边求面积的公式，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减上，余四约之，为实，一为从隅，开平方得积．”若把以上这段文字写成公式，即 $S = \sqrt{\frac{1}{4} [c^{2} a^{2} - {(\frac{c^{2} + a^{2} - b^{2}}{2})}^{2}]}$ ．现有△ $A B C$ 满足 $s i n A ： s i n B ： s i n C = 2 ： 3 ： \sqrt{7}$ ，且 $S_{△ A B C} = 6 \sqrt{3}$ ，请判断下列命题正确的是（）

A、△ $A B C$ 周长为 $5 + \sqrt{7}$ B、 $C = \frac{π}{3}$ C、△ $A B C$ 的外接圆半径为 $\frac{2 \sqrt{21}}{3}$ D、△ $A B C$ 中线 $C D$ 的长为 $\frac{\sqrt{19}}{2}$

查看试题解析
12. 如图，已知点G为 $△ A B C$ 的重心，点D，E分别为AB，AC上的点，且D，G，E三点共线， $\vec{A D} = m \vec{A B}$ ， $\vec{A E} = n \vec{A C}$ ， $m > 0$ ， $n > 0$ ，记 $△ A D E$ ， $△ A B C$ ，四边形BDEC的面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，则（）

A、 $\frac{1}{m} + \frac{1}{n} = 3$ B、 $\frac{S_{1}}{S_{2}} = m n$ C、 $\frac{S_{1}}{S_{3}} \geq \frac{4}{5}$ D、 $\frac{S_{1}}{S_{3}} \leq \frac{4}{5}$

查看试题解析

三、填空题

13. 若复数z满足 $z + i = \frac{i - 3}{i}$ ，则 $| z | =$ .

查看试题解析
14. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $(2 c - b) c o s A = a c o s B$ ， $a = 2$ ，则 $△ A B C$ 外接圆的面积为.

查看试题解析
15. 某热爱飞镖的小朋友用纸片折出如图所示的十字飞镖ABCDEFGH，该十字飞镖由四个全等的三角形和一个正方形组成．在△ABC中， $A B = \sqrt{13}$ ， $A C = \sqrt{5}$ ， BC＝4，边DE上有4个不同的点 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ ，且 $P_{1} P_{2} = P_{2} P_{3} = P_{3} P_{4} = 2 E P_{1} = 2 D P_{4}$ ，记 $a_{i} = \vec{B C} \cdot \vec{B P_{i}} (i = 1 ， 2 ， 3 ， 4)$ ，则 $a_{1} + a_{2} + a_{3} + a_{4} =$ .

查看试题解析
16. 连接正方体相邻各面的中心(中心是指正方形的两条对角线的交点)后所得到了一个几何体，设正方体的棱长为 $a$ ，则该几何体的表面积为，该几何体的体积为.

查看试题解析

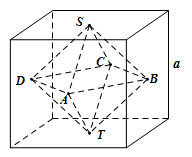
四、解答题

17. 已知单位向量 $\vec{e_{1}} ， \vec{e_{2}}$ 的夹角为 $\frac{2 π}{3}$ ，向量 $\vec{a} = \vec{e_{1}} - x \vec{e_{2}}$ ，向量 $\vec{b} = 3 \vec{e_{1}} + 2 \vec{e_{2}}$ .

(1)、若 $\vec{a}$ ∥ $\vec{b}$ ，求x的值；

(2)、若 $\vec{a} ⊥ \vec{b}$ ，求 $| \vec{a} |$ .

查看试题解析
18. $△ A B C$ 的内角 $A$ 、 $B$ 、 $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，已知 $a^{2} = b c o s C + c c o s B$ .

(1)、求 $a$ ；

(2)、若 $A = \frac{π}{3}$ ， $△ A B C$ 的面积为 $\frac{\sqrt{3}}{4}$ ，求 $△ A B C$ 的周长.

查看试题解析
19. 已知向量 $\vec{a} = (\cos x + \sin x ， \sqrt{3} \cos x)$ ， $\vec{b} = (\cos x - \sin x ， - 2 \sin x)$ ，记函数 $f (x) = \vec{a} \cdot \vec{b}$ .

(1)、求函数 $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上的取值范围；

(2)、若 $g (x) = f (x + t)$ 为偶函数，求 $| t |$ 的最小值.

查看试题解析
20. 如图所示是在圆锥内部挖去一正四棱柱所形成的几何体，该正四棱柱上底面的四顶点在圆锥侧面上，下底面落在圆锥底面内，已知圆锥侧面积为15π，底面半径为 $r = 3$ .
（Ⅰ）若正四棱柱的底面边长为 $a = \sqrt{2}$ ，求该几何体的体积；
（Ⅱ）求该几何体内正四棱柱侧面积的最大值.

查看试题解析
21. 已知 $a$ ， $b$ ， $c$ 分别为 $Δ A B C$ 内角A，B，C的对边，若 $Δ A B C$ 同时满足下列四个条件中的三个：① $\frac{b - a}{c} = \frac{2 \sqrt{6} a + 3 c}{3 (a + b)}$ ；② $c o s 2 A + 2 c o s^{2} \frac{A}{2} = 1$ ；③ $a = \sqrt{6}$ ；④ $b = 2 \sqrt{2}$ .

(1)、满足有解三角形的序号组合有哪些？

(2)、在（1）所有组合中任选一组，并求对应 $Δ A B C$ 的面积.
（若所选条件出现多种可能，则按计算的第一种可能计分）

查看试题解析
22. 已知O为坐标原点，对于函数 $f (x) = a \sin x + b \cos x$ ，称向量 $\vec{O M} = (a ， b)$ 为函数 $f (x)$ 的相伴特征向量，同时称函数 $f (x)$ 为向量 $\vec{O M}$ 的相伴函数.

(1)、设函数 $g (x) = \sin (x + \frac{5 π}{6}) - \sin (\frac{3 π}{2} - x)$ ，试求 $g (x)$ 的相伴特征向量 $\vec{O M}$ ；

(2)、记向量 $\vec{O N} = (1 ， \sqrt{3})$ 的相伴函数为 $f (x)$ ，求当 $f (x) = \frac{8}{5}$ 且 $x \in (- \frac{π}{3} ， \frac{π}{6})$ ， $\sin x$ 的值；

(3)、已知 $A (- 2 ， 3)$ ， $B (2 ， 6)$ ， $\vec{O T} = (- \sqrt{3} ， 1)$ 为 $h (x) = m \sin (x - \frac{π}{6})$ 的相伴特征向量， $φ (x) = h (\frac{x}{2} - \frac{π}{3})$ ，请问在 $y = φ (x)$ 的图象上是否存在一点P，使得 $\vec{A P} ⊥ \vec{B P}$ .若存在，求出P点坐标；若不存在，说明理由.

查看试题解析