福建省三明市五县2021-2022学年高一下学期数学联合质检考试（期中）试卷

试卷更新日期：2022-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $z = \frac{2}{1 - i}$ （ $i$ 为虚数单位），则（）

A、 $z$ 的虚部为 $i$ B、 $| z | = 2$ C、 $\bar{z} = - 1 + i$ D、 $z^{2}$ 为纯虚数

查看试题解析
2. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{2}{3} π$ ， $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ，则 $| \vec{a} - 2 \vec{b} | =$ （）

A、 $2 \sqrt{3}$ B、3 C、 $\sqrt{3}$ D、12

查看试题解析
3. 已知向量 $\vec{a}$ ， $\vec{b}$ ，且 $\vec{A B} = \vec{a} + 2 \vec{b}$ ， $\vec{B C}$ $= - 5 \vec{a} + 6 \vec{b}$ ， $\vec{C D} = 7 \vec{a} - 2 \vec{b}$ ，则一定共线的三点是（）

A、A，B，D B、A，B，C C、B，C，D D、A，C，D

查看试题解析
4. 如图， $A B = 1 ， A C = 3 ， ∠ A = 90 ° ， \vec{C D} = 2 \vec{D B}$ ，则 $\vec{A D} \cdot \vec{A B} =$ （）

A、 $\frac{4}{3}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
5. 已知a、b、c分别是△ABC三个内角A、B、C的对边，b＝ $\sqrt{7}$ ， c＝ $\sqrt{3}$ ， B＝ $\frac{π}{6}$ ，那么a等于（）

A、1 B、2 C、4 D、1或4

查看试题解析
6. 在日常生活中，我们常常会看到两个人共提一个行李包的情景，若行李包所受的重力为 $G$ ，两个拉力分别为 $F_{1}$ ， $F_{2}$ ，且 $| F_{1} | = | F_{2} |$ ， $F_{1}$ 与 $F_{2}$ 夹角为 $θ$ ，当两人拎起行李包时，下列结论正确的是（）

A、 $| G | = | F_{1} | + | F_{2} |$ B、当 $θ = \frac{π}{2}$ 时， $| F_{1} | = \frac{\sqrt{2}}{2} | G |$ C、当 $θ$ 角越大时，用力越省 D、当 $| F_{1} | = | G |$ 时， $θ = \frac{π}{3}$

查看试题解析
7. 已知非零向量 $\overset{⇀}{A B}$ 与 $\overset{⇀}{A C}$ 满足 $(\frac{\overset{⇀}{A B}}{| \overset{⇀}{A B} |} + \frac{\overset{⇀}{A C}}{| \overset{⇀}{A C} |}) \cdot \overset{⇀}{B C} = 0$ 且 $\frac{\overset{⇀}{A B}}{| \overset{⇀}{A B} |} \cdot \frac{\overset{⇀}{A C}}{| \overset{⇀}{A C} |} = \frac{1}{2}$ ，则 $Δ A B C$ 为（）

A、等边三角形 B、直角三角形 C、等腰非等边三角形 D、等腰直角三角形

查看试题解析
8. 已知在锐角 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，且满足 $a (1 + c o s B) = b c o s A$ ，则 $\frac{s i n B}{s i n^{2} A}$ 的取值范围是（）

A、 $(2 ， 2 \sqrt{3})$ B、 $(\sqrt{3} ， 2)$ C、 $(0 ， \frac{2 \sqrt{3}}{3})$ D、 $(2 ， + ∞)$

查看试题解析

二、多选题

9. 已知向量 $\vec{a} = (1 ， 1)$ ， $\vec{b} = (0 ， - 2)$ ，则以下结论正确的有（）

A、 $\vec{a} \cdot \vec{b} = | \vec{b} |$ B、 $(2 \vec{a} + \vec{b}) ⊥ \vec{b}$ C、 $\vec{a} - \vec{b}$ 与 $\vec{a}$ 可以作为一组基底 D、 $\vec{a} / / (\vec{a} + \vec{b})$

查看试题解析
10. 已知 $i$ 为虚数单位，则下面命题正确的是（）

A、若复数 $z = 3 + i$ ，则 $\frac{1}{z} = \frac{3}{10} - \frac{i}{10}$ . B、复数 $z$ 满足 $| z - 2 i | = 1$ ， $z$ 在复平面内对应的点为 $(x ， y)$ ，则 $x^{2} + {(y - 2)}^{2} = 1$ . C、若复数 $z_{1}$ ， $z_{2}$ 满足 $z_{1} = \bar{z_{2}}$ ，则 $z_{1} z_{2} \geq 0$ . D、复数 $z = - 3 i + 1$ 的虚部是1.

查看试题解析
11. 不解三角形，根据已知条件，判断三角形的解的个数.下列说法中正确的是（）

A、 $a = 7$ ， $b = 14$ ， $A = 30 °$ ， $△ A B C$ 有一解 B、 $a = 3$ ， $c = 5$ ， $B = 120 °$ ， $△ A B C$ 有一解 C、 $a = 6$ ， $b = 9$ ， $A = 45 °$ ， $△ A B C$ 有两解 D、 $a = 9$ ， $b = 10$ ， $A = 60 °$ ， $△ A B C$ 有两解

查看试题解析
12. 给出下列命题，其中正确的选项有（）

A、非零向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = | \vec{b} | = | \vec{a} - \vec{b} |$ ，则 $\vec{a}$ ， $\vec{a} + \vec{b}$ 的夹角为30° B、若 $s i n 2 A = s i n 2 B$ ，则 $△ A B C$ 为等腰三角形 C、若 $\vec{a}$ 与 $\vec{b}$ 平行， $\vec{a}$ 在 $\vec{b}$ 方向上的投影向量为 $\pm \frac{| \vec{a} |}{| \vec{b} |} \vec{b}$ D、已知 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (1 ， 1)$ ，且 $\vec{a}$ 与 $\vec{a} + λ \vec{b}$ 夹角为锐角，则 $λ \in (- \frac{5}{3} ， + \infty)$

查看试题解析

三、填空题

13. 在 $△ A B C$ 中，若 $s i n A ： s i n B ： s i n C = 4 ： \sqrt{21} ： 5$ ，则 $B =$ .

查看试题解析
14. 已知复数 $z$ 满足 $| z | = 2$ ，则复数 $| z + 1 + \sqrt{3} i |$ 的最大值为．

查看试题解析
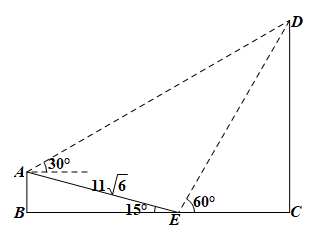
15. 2021年5月27日，以“绿色秦巴，开放互赢”为主题的第三届秦巴山区绿色农林产业投资贸易洽谈会在四川省巴中市开幕，会场设在刚刚竣工的川东北最大的综合体育场——巴中市体育中心，即民间所说的“兴文鸟巢”，能被邀请到现场观礼是无比的荣耀．如图，在坡度为15º的观礼台上，某一列座位与旗杆在同一个垂直于地面的平面上，在该列的第一排和最后一排测得旗杆顶端的仰角分别为60º和30º，且第一排和最后一排的距离为 $11 \sqrt{6}$ 米，则旗杆的高度为米．

查看试题解析
16. 如图，已知正方形 $A B C D$ 的边长为2，过中心 $O$ 的直线 $l$ 与两边 $A B$ ， $C D$ 分别交于点 $M$ ， $N$ ，若 $Q$ 是 $B C$ 的中点，则 $\vec{Q M} \cdot \vec{Q N}$ 的取值范围是；若 $P$ 是平面上一点，且满足 $2 \vec{O P} = λ \vec{O B} + (1 - λ) \vec{O C}$ ，则 $\vec{P M} \cdot \vec{P N}$ 的最小值是.

查看试题解析

四、解答题

17. 已知复数 $z = (m^{2} - 2 m - 3) + (m^{2} + m - 2) i ， (m \in R)$ ．

(1)、若 $z > 0$ ，求m的值；

(2)、若z是纯虚数，求 $z \cdot \bar{z}$ 的值．

查看试题解析
18. 已知平面向量 $\vec{a} = (3 ， 4)$ ， $\vec{b} = (9 ， x)$ ， $\vec{c} = (4 ， y)$ ，且 $\vec{a} / / \vec{b}$ ， $\vec{a} ⊥ \vec{c}$ .

(1)、求 $\vec{b}$ 和 $\vec{c}$ ：

(2)、若 $\vec{m} = 2 \vec{a} - \vec{b}$ ， $\vec{n} = \vec{a} + \vec{c}$ ，求向量 $\vec{m}$ 与向量 $\vec{n}$ 的夹角的大小.

查看试题解析
19. 在① $s i n B - s i n C = s i n (A - C)$ ；② $c o s A + c o s 2 A = 0$ ；③ $2 a c o s A = b c o s C + c c o s B$ 这三个条件中任选一个，补充在下面问题中，并解答.
问题：已知 $△ A B C$ 的内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ， ____.

(1)、求A；

(2)、若 $a = 2 ， △ A B C$ 的面积是 $\frac{\sqrt{3}}{2}$ ，求 $△ A B C$ 的周长.
（注：如果选择多个条件分别解答，按第一个解答计分）

查看试题解析
20. 如图所示， $Δ A B C$ 是边长为 $1$ 的正三角形，点 $P_{1} ， P_{2} ， P_{3}$ 四等分线段 $B C$ ．

(1)、求 $\overset{⇀}{A B} \cdot \overset{⇀}{A P_{1}} + \overset{⇀}{A P_{1}} \cdot \overset{⇀}{A P_{2}}$ 的值；

(2)、若点Q是线段 $A P_{3}$ 上一点，且 $\overset{⇀}{A Q} = \frac{1}{12} \overset{⇀}{A B} + m \overset{⇀}{A C}$ ，求实数m的值．

查看试题解析
21. 某沿海城市附近海面有一台风，据观测，台风中心位于城市正南方向 $200 k m$ 的海面 $P$ 处，并正以 $20 k m / h$ 的速度向北偏西 $θ$ 方向移动（其中 $c o s θ = \frac{19}{20}$ ），台风当前影响半径为 $10 k m$ ，并以 $10 k m / h$ 的速度不断增大，问几小时后该城市开始受到台风影响？影响时间多长？

查看试题解析
22. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $S_{△ A B C} = \frac{\sqrt{3}}{2} \vec{A B} \cdot \vec{A C}$ ， $a = 3$ ，若点 $D$ 在边 $B C$ 上，且 $B D = \frac{1}{3} B C$ .

(1)、求 $A$ 的值；

(2)、求 $A D$ 的最大值.

查看试题解析