山东省临沂市2021-2022学年高二下学期数学期中考试试卷

试卷更新日期：2022-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 从A地到B地要经过C地，已知从A地到C地有三条路，从C地到B地有四条路，则从A地到B地不同的走法种数是（）

A、7 B、9 C、12 D、16

查看试题解析
2. 已知 $P (A B) = \frac{2}{15}$ ， $P (A) = \frac{2}{5}$ ，那么 $P (B | A)$ 等于（）

A、 $\frac{4}{75}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
3. 在 $(1 + x) + {(1 + x)}^{2} + {(1 + x)}^{3} + \dots + {(1 + x)}^{9}$ 的展开式中， $x^{2}$ 的系数等于（）

A、280 B、300 C、210 D、120

查看试题解析
4. 在“志愿和平”活动中，某校高二年级3名男教师和4名女教师参与社区防控新冠肺炎疫情的志愿服务.根据岗位需求应派3人巡视商户，且至少有1名男教师；另外4人测量出入人员体温.则这7名教师不同的安排方法有（）

A、15种 B、18种 C、31种 D、45种

查看试题解析
5. 某市高二年级男生的身高 $ξ$ (单位： $cm$ )近似服从正态分布 $ξ \sim N (170 ， 25)$ ，则随机选择名本市高二年级的男生身高在 $[165 ， 180]$ 内的概率为（）
附：随机变量符合正态分布 $ξ \sim N (μ ， σ^{2})$ ，则 $P (μ - σ < ξ < μ + σ) = 0.6827$ ， $\begin{array}{r} P (μ - 2 σ < ξ < μ + 2 σ) = 0.9545 ， P (μ - 3 σ < ξ < μ + 3 σ) = 0.9973 \end{array}$

A、0.84 B、0.8186 C、0.9759 D、0.4772

查看试题解析
6. 设函数 $f (x) = \ln x + a x^{2} - \frac{3}{2} x$ ，若 $x = 1$ 是函数 $f (x)$ 是极大值点，则函数 $f (x)$ 的极小值为（）

A、 $\ln 2 - 2$ B、 $\ln 2 - 1$ C、 $\ln 3 - 2$ D、 $\ln 3 - 1$

查看试题解析
7. 为了研究某校男生的脚长 $x$ (单位； $cm$ )和身高 $y$ (单位： $cm$ )的关系，从该校随机抽取20名男生，根据测量数据的散点图可以看出 $y$ 与 $x$ 之间有线性相关关系.设 $y$ 关于 $x$ 的经验回归方程为 $\hat{y} = \hat{b} x + \hat{a}$ .已知 $\sum_{i = 1}^{20} x_{i} = 460$ ， $\sum_{i = 1}^{20} y_{i} = 3240$ ， $\hat{b} = 4$ ，该校某男生的脚长为 $25.5 cm$ ，据此估计其身高为（）

A、 $164 cm$ B、 $168 cm$ C、 $172 cm$ D、 $176 cm$

查看试题解析
8. 已知可导函数 $f (x)$ 的导函数为 $f^{'} (x)$ ， $f (0) = 2021$ ，若对任意的 $x \in R$ ，都有 $f (x) < f^{'} (x)$ ，则不等式 $f (x) < 2021 e^{x}$ 的解集为（）

A、 $(0 ， + ∞)$ B、 $(\frac{2021}{e^{2}} ， + \infty)$ C、 $(- \infty ， \frac{2021}{e^{2}})$ D、 $(- \infty ， 0)$

查看试题解析

二、多选题

9. 定义在R上的可导函数 $y = f (x)$ 的导函数的图象如图所示，以下结论正确的是（）

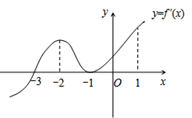A、-3是 $f (x)$ 的一个极小值点； B、-2和-1都是 $f (x)$ 的极大值点； C、 $f (x)$ 的单调递增区间是 $(- 3 ， + \infty)$ ； D、 $f (x)$ 的单调递减区间是 $(- \infty ， - 3)$ ．

查看试题解析
10. 如图，标注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点 $A$ 向结点 $B$ 传递消息，信息可以分开沿不同的路线同时传递，小圆圈表示网络的结点，结点之间的连线表示他们有网线相连，则单位时间内传递的信息量可以为（）

A、18 B、19 C、24 D、26

查看试题解析
11. 离散型随机变量 $X$ 的分布列如下表，若离散型随机变量 $Y$ 满足 $Y = 2 X + 1$ ，则下列结果正确的有（）
$X$
0
1
2
3
4
$P$
q
0.4
0.1
0.2
0.2

A、 $q = 0.1$ B、 $E (X) = 2$ ， $D (X) = 1.4$ C、 $E (X) = 2$ ， $D (X) = 1.8$ D、 $E (Y) = 5$ ， $D (Y) = 7.2$

查看试题解析
12. 已知函数 $f (x) = e^{x} - 1$ ，对于满足 $0 < x_{1} < x_{2} < e$ 的任意 $x_{1}$ ， $x_{2}$ ，下列结论中正确的是（）

A、 $(x_{2} - x_{1}) [f (x_{2}) - f (x_{1})] < 0$ B、 $x_{2} f (x_{1}) > x_{1} f (x_{2})$ C、 $f (x_{2}) - f (x_{1}) > x_{2} - x_{1}$ D、 $\frac{f (x_{1}) + f (x_{2})}{2} > f (\frac{x_{1} + x_{2}}{2})$

查看试题解析

三、填空题

13. 离散型随机变量 $ξ$ 的分布列，且 $E (ξ) = 2$ ，则 $p_{1} =$ ； $p_{2} =$ ．
$ξ$
1
2
3
p
$p_{1}$
$p_{2}$
$\frac{1}{4}$

查看试题解析
14. 高三某位同学参加物理、化学科目的等级考，已知这位同学在物理、化学科目考试中达A的概率分别为 $\frac{1}{2}$ 、 $\frac{2}{3}$ ，这两门科目考试成绩的结果互不影响，则这位考生至少得1个A的概率为.

查看试题解析
15. 已知 $(1 + x) {(2 - x)}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{3} =$ ．

查看试题解析
16. 已知函数 $f (x) = e^{x} - a x^{2}$ ， $a \in R$ ，现有下列结论：
① $f (x)$ 至多有三个零点；
② $\exists a \in [2 ， + \infty)$ ，使得 $\forall x \in (0 ， + \infty)$ ， $f (x) > 0$ ；
③当 $a \in [0 ， \frac{e}{2}]$ 时， $f (x)$ 在 $R$ 上单调递增.
其中正确的结论序号是.

查看试题解析

四、解答题

17. 已知 $(2 x - 1)^{n} (n \in N^{*})$ 的二项展开式中二项式系数之和为256.

(1)、求 $n$ 的值；

(2)、求该展开式中 $x^{3}$ 项的系数.

查看试题解析
18. 已知函数 $f (x) = (x^{2} - 3 x + 1) e^{x}$ ．

(1)、求 $f (x)$ 的单调区间；

(2)、求 $f (x)$ 在区间 $[- 2 ， 0]$ 上的最大值和最小值．

查看试题解析
19. 某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（ $x$ 元）试销 $1$ 天，得到如表单价 $x$ （元）与销量 $y$ （册）数据：
单价 $x$ （元）
18
19
20
21
22
销量 $y$ （册）
61
56
50
48
45
附： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ， $\sum_{i = 1}^{5} x_{i} y_{i} = 5160$ ， $\sum_{i = 1}^{5} x_{i}^{2} = 2010$ ．

(1)、根据表中数据，请建立 $y$ 关于 $x$ 的回归直线方程：

(2)、预计今后的销售中，销量 $y$ （册）与单价 $x$ （元）服从（1）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？

查看试题解析
20. 2020年开始，国家逐步推行全新的高考制度．新高考不再分文理科，采用3+3模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣爱好等因素，在政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科目满分100分．为了应对新高考，某高中从高一年级1000名学生（其中男生550人，女生450人）中，根据性别采用分层抽样的方法从中抽取100名学生进行调查．
附参考公式及数据： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$
$P (K^{2} \geq k_{0})$
0.05
0.01
$k_{0}$
3.841
6.635

(1)、学校计划在高二上学期开设选修中的“物理”和“政治”两个科目，为了了解学生对这两个科目的选课情况，对抽取到的100名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目），下表是根据调查结果得到的2×2列联表．请将列联表补充完整，并判断是否有95%的把握认为选择科目与性别有关？说明你的理由；

选择“物理”
选择“政治”
总计
男生
10
女生
30
总计

(2)、在（1）的条件下，从选择“政治”的学生中抽取5人，再从这5人中随机抽取2 人，设这2人中男生的人数为 $X$ ，求 $X$ 的分布列及数学期望．

查看试题解析
21. 流行性感冒多由病毒引起，据调查，空气月平均相对湿度过大或过小时，都有利于一些病毒繁殖和传播．科学测定，当空气月平均相对湿度大于65%或小于40%时，有利于病毒繁殖和传播．下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度．

第一季度
第二季度
第三季度
第四季度
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
甲地
54%
39%
46%
54%
56%
67%
64%
66%
78%
72%
72%
59%
乙地
38%
34%
31%
42%
54%
66%
69%
65%
62%
70%
a%
b%

(1)、从上表12个月中，随机取出1个月，求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率；

(2)、从上表第一季度和第二季度的6个月中随机取出2个月，记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为X，求X的分布列；

(3)、若 $a + b = 108$ ，设乙地上表12个月的空气月平均相对湿度的中位数为M，求M的最大值和最小值．（只需写出结论）

查看试题解析
22. 设函数 $f (x) = a e^{x} - x - 1 ， a \in R$ .

(1)、当 $a = 1$ 时，求 $f (x)$ 的单调区间；

(2)、当 $x \in (0 ， + \infty)$ 时， $f (x) > 0$ 恒成立，求 $a$ 的取值范围；

(3)、求证：当 $x \in (0 ， + \infty)$ 时， $l n \frac{e^{x} - 1}{x} > \frac{x}{2}$ .

查看试题解析

单价 $x$ （元）	18	19	20	21	22
销量 $y$ （册）	61	56	50	48	45

	选择“物理”	选择“政治”	总计
男生		10
女生	30
总计

	第一季度			第二季度			第三季度			第四季度
	1月	2月	3月	4月	5月	6月	7月	8月	9月	10月	11月	12月
甲地	54%	39%	46%	54%	56%	67%	64%	66%	78%	72%	72%	59%
乙地	38%	34%	31%	42%	54%	66%	69%	65%	62%	70%	a%	b%

$X$	0	1	2	3	4
$P$	q	0.4	0.1	0.2	0.2

$ξ$	1	2	3
p	$p_{1}$	$p_{2}$	$\frac{1}{4}$

$P (K^{2} \geq k_{0})$	0.05	0.01
$k_{0}$	3.841	6.635