河南省郑州市十校2021-2022学年高二下学期理数期中联考试卷
试卷更新日期:2022-04-25 类型:期中考试
一、单选题
-
1. 已知复数 , 则复数的虚部为( )A、-1 B、1 C、 D、2. 的导数是( )A、 B、 C、 D、03. 已知 ,则 的值( )A、都大于1 B、都小于1 C、至多有一个不小于1 D、至少有一个不小于14. 有如下的演绎推理:“因为对数函数当时在上是增函数;已知是对数函数,所以在上是增函数”的结论是错误的,错误的原因是( )A、大前提错误 B、小前提错误 C、大小前提都错误 D、推理形式错误5. ( )A、 B、 C、 D、6. 在平面几何里,有勾股定理:“设的两边 , 互相垂直,则有“,扩展到空间,类比平面几何的勾股定理,”设三棱锥的三个侧面 , , ABD两两互相垂直,则可得( )A、 B、 C、 D、7. 用数学归纳法证明“不等式对一切正整数恒成立”的第二步中,已经假设时不等式成立,推理成立的步骤中用到了放缩法,这个放缩过程主要是证明( )A、 B、 C、 D、8. 为了宣传2022年北京冬奥会和冬残奥会,某学校决定派小明和小李等共5名志愿者将两个吉祥物“冰墩墩”和“雪容融”安装在学校的体育广场,每人参与且只参与一个吉祥物的安装,每个吉祥物至少由两名志愿者安装.若小明和小李必须安装相同的吉祥物,则不同的分配方案种数为( )A、8 B、10 C、12 D、149. 给出定义:设是函数的导函数,是函数的导函数,若方程有实数解 , 则称点为函数的“拐点”.已知函数的拐点是 , 则点( )A、在直线上 B、在直线上 C、在直线上 D、在直线上10. 设点是函数图象上的任意一点,点P处切线的倾斜角为 , 则角的取值范围是( )A、 B、 C、 D、11. 著名数学家华罗庚曾说“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休”,在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数图象特征,则函数的图像大致是( )A、
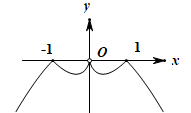 B、
B、 C、
C、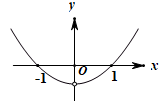 D、
D、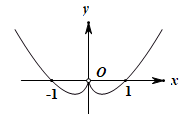 12. 已知函数 , 若对恒成立,则实数的取值范围为( )A、 B、 C、 D、
12. 已知函数 , 若对恒成立,则实数的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 若 , 则的值 .14. 设复数z,满足 , , , 则 .15. 某工程队有5项工程需要单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后立即进 行那么安排这5项工程的不同排法种数是 .(用数字作答)
16. 若函数有极值点 , , 则关于的方程 +的不同实数根的个数是.三、解答题
-
17. 已知复数 , , .(1)、若为纯虚数,求实数的值;(2)、在复平面内,若对应的点在第四象限,对应的点在第二象限,求实数的取值范围.18. 已知的二项展开式中所有奇数项的系数之和为512.(1)、求展开式的所有有理项(指数为整数);(2)、求展开式中项的系数.19. 设函数 , 曲线在点处的切线方程为.(1)、求的解析式;(2)、证明:曲线上任一点处的切线与直线和直线所围成的三角形的面积为定值,并求此定值.