2022年浙教版数学九上复习阶梯训练：第2章简单事件的概率（优生集训）

试卷更新日期：2022-04-22 类型：复习试卷

进入出卷网下载

一、综合题

1. 十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策，这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措．二孩政策出台后，某家庭积极响应政府号召，准备生育两个孩子（生男生女机会均等，且与顺序有关）．

(1)、该家庭生育两胎，假设每胎都生育一个小孩，求这两个小孩恰好是1男1女的概率；

(2)、该家庭生育两胎，假如第一胎生育一个小孩，其第二胎生育一对双胞胎，请你用画树状图或列表的方法，求这三个小孩中至少有一个女孩的概率．

查看试题解析
2. 小美周末来到公园，发现在公园一角有一种“守株待兔”游戏．游戏设计者提供了一只兔子和一个有A，B，C，D，E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定：①玩家只能将小兔从A、B两个出入口放入，②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则每玩一次应付费3元．

(1)、请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率；

(2)、假设有1000人次玩此游戏，估计游戏设计者可赚多少元？

查看试题解析
3. 某中学需在短跑、跳远、乒乓球、跳高四类体育项目中各选一名同学参加中学生运动会，根据平时成绩，把各项目进入复选的人员情况绘制成不完整的统计图、表如下：
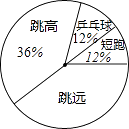
复选人员扇形统计图：
复选人员统计表：
项目/人数/性别
男
女
短跑
1
2
跳远
a
6
乒乓球
2
1
跳高
3
b

(1)、求a、b的值；

(2)、求扇形统计图中跳远项目对应圆心角的度数；

(3)、用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率．

查看试题解析
4. 某学校“体育课外活动兴趣小组”，开设了以下体育课外活动项目：A．足球 B．乒乓球C．羽毛球 D．篮球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

(1)、这次被调查的学生共有人，在扇形统计图中“D”对应的圆心角的度数为；

(2)、请你将条形统计图补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加市里组织的乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

查看试题解析
5. 某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：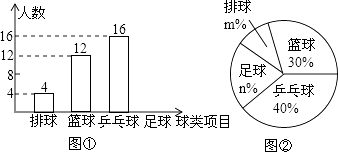

(1)、九（1）班的学生人数为__ ，并把条形统计图补充完整；

(2)、扇形统计图中m=10 ， n=20 ，表示“足球”的扇形的圆心角是多少度；

(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

查看试题解析
6.
“中国梦”关系每个人的幸福生活，为展现巴中人追梦的风采，我市某中学举行“中国梦•我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．

(1)、参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；

(2)、补全条形统计图；

(3)、组委会决定从本次比赛中获得B等级的学生中，选出2名去参加市中学生演讲比赛，已知A等级中男生有1名，请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率．

查看试题解析
7.
”切实减轻学生课业负担”是我市作业改革的一项重要举措．某中学为了解本校学生平均每天的课外作业时间，随机抽取部分学生进行问卷调查，并将调查结果分为A、B、C、D四个等级，A：1小时以内；B：1小时﹣﹣1.5小时；C：1.5小时﹣﹣2小时；D：2小时以上．根据调查结果绘制了如图所示的两种不完整的统计图，请根据图中信息解答下列问题：

(1)、该校共调查了学生．

(2)、请将条形统计图补充完整．

(3)、表示等级A的扇形圆心角α的度数是．

(4)、在此次调查问卷中，甲、乙两班各有2人平均每天课外作业量都是2小时以上，从这4人中人选2人去参加座谈，用列表或画树状图的方法求选出的2人来自不同班级的概率．

查看试题解析
8.
为了解全校学生上学的交通方式，该校九年级（8）班的5名同学联合设计了一份调查问卷，对该校部分学生进行了随机调查．按A（骑自行车）、B（乘公交车）、C（步行）、D（乘私家车）、E（其他方式）设置选项，要求被调查同学从中单选．并将调查结果绘制成条形统计图1和扇形统计图2，根据以上信息，解答下列问题：

(1)、本次接受调查的总人数是人，并把条形统计图补充完整；

(2)、在扇形统计图中，“步行”的人数所占的百分比是　，“其他方式”所在扇形的圆心角度数是；

(3)、已知这5名同学中有2名女同学，要从中选两名同学汇报调查结果．请你用列表法或画树状图的方法，求出恰好选出1名男生和1名女生的概率．

查看试题解析
9. 一个不透明的布袋里装有4个大小，质地都相同的乒乓球，球面上分别标有数字1，-2，3，-4，小明先从布袋中随机摸出一个球（不放回去），再从剩下的3个球中随机摸出第二个乒乓球．

(1)、共有几种可能的结果？

(2)、请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率．

查看试题解析
10.
学校开展综合实践活动中，某班进行了小制作评比，作品上交时间为5月11日至5月30日，评委们把同学们上交作品的件数按5天一组分组统计，绘制了频数分布直方图如下，小长方形的高之比为：2：5：2：1．现已知第二组的上交作品件数是20件．求：

(1)、此班这次上交作品共多少件？

(2)、评委们一致认为第四组的作品质量都比较高，现从中随机抽取2件作品参加学校评比，小明的两件作品都在第四组中，他的两件作品都被抽中的概率是多少？（请写出解答过程）

查看试题解析
11. 甲．乙．丙三个事件发生的概率分别为0.5，0.1，0.9，它们各与下面的哪句话相配．

(1)、发生的可能性很大，但不一定发生；

(2)、发生的可能性很小；

(3)、发生与不发生的可能性一样．

查看试题解析
12. 一个口袋中有9个红球和若干个白球，在不允许将球倒出来数的前提下，小明采用如下的方法估算其中白球的个数：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色…，小明重复上述过程共摸了100次，其中40次摸到白球，请回答：

(1)、口袋中的白球约有多少个？

(2)、有一个游乐场，要按照上述红球、白球的比例配置彩球池，若彩球池里共有1200个球，则需准备多少个红球？

查看试题解析
13. 从“不太可能”、“不可能”、“很有可能”和“必然”中选择适当的词描述下列事件．

(1)、在直线上任取一点作射线，得到两个和为180°的角.

(2)、任画两条直线与另一条直线都相交，得到两个彼此相等的同位角；

(3)、小强对数学很感兴趣，常钻研教材内容，在数学测验中取得好成绩；

(4)、在电话上随机拨一串数字，刚好打通了好朋友的电话；

(5)、互为倒数的两个有理数符号相同．

查看试题解析
14. 中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：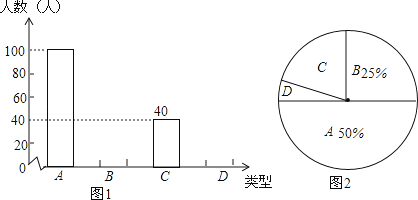

(1)、此次抽样调查中，共调查了名学生.

(2)、将图1、图2补充完整；

(3)、现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

查看试题解析
15. 有三张卡片（形状、大小、颜色、质地都相等），正面分别写上整式x²+1，﹣x²﹣2，3．将这三张卡片背面向上洗匀，从中任意抽取一张卡片，记卡片上的整式为A，再从剩下的卡片中任意抽取一张，记卡片上的整式为B，于是得到代数式 $\frac{A}{B}$ ．

(1)、请用画树状图或列表的方法，写出代数式 $\frac{A}{B}$ 所有可能的结果；

(2)、求代数式 $\frac{A}{B}$ 恰好是分式的概率．

查看试题解析
16. 在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，他们的形状、大小、质地等完全相同．小兰先从盒子里随机取出一个小球，记下数字为x，放回盒子，摇匀后，再由小田随机取出一个小球，记下数字为y.

(1)、用列表法或画树状图法表示出（x，y）的所有可能出现的结果；

(2)、求小兰、小田各取一次小球所确定的点（x，y）落在反比例函数y= $\frac{6}{x}$ 的图象上的频率；

(3)、求小兰、小田各取一次小球所确定的数x，y满足y< $\frac{6}{x}$ 的概率.

查看试题解析
17. 用4张相同的小纸条做成甲、乙、丙、丁4支签，放在一个盒子中，搅匀后先从盒子中任意抽出1支签（不放回），再从剩余的3支签中任意抽出1支签．

(1)、用树状图或列表等方法列出所有可能出现的结果。

(2)、求抽出的两支签中，1支为甲签、1支为丁签的概率。

查看试题解析
18. 为了提高中学生身体素质，学校开设了A：篮球、B：足球、C：跳绳、D：羽毛球四种体育活动，为了解学生对这四种体育活动的喜欢情况，在全校随机抽取若干名学生进行问卷调查（每个被调查的对象必须选择而且只能在四种体育活动中选择一种），将数据进行整理并绘制成以下两幅统计图（未画完整）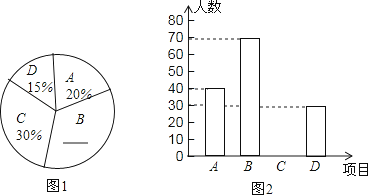

(1)、这次调查中，一共调查了名学生。

(2)、请补全两幅统计图。

(3)、若有3名喜欢跳绳的学生，1名喜欢足球的学生组队外出参加一次联谊活动，欲从中选出2人担任组长（不分正副），求一人是喜欢跳绳、一人是喜欢足球的学生的概率。

查看试题解析
19. 在“阳光体育”活动时间，小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛，要从中选出两位同学打第一场比赛

(1)、若已确定小英打第一场，再从其余三位同学中随机选取一位，求恰好选中小丽同学的概率

(2)、用画树状图或列表的方法，求恰好选中小敏、小洁两位同学进行比赛的概率

查看试题解析
20.
某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：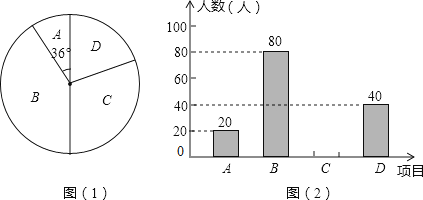

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图（2）补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率.（用树状图或列表法解答）

查看试题解析
21. 随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：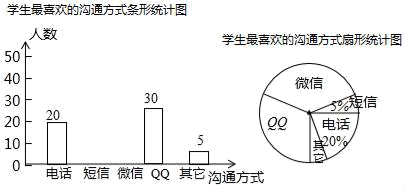

(1)、这次统计共抽查了名学生；在扇形统计图中，表示“QQ”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率．说明：设“微信，QQ和电话”三种沟通方式分别用字母W，Q和D表示．）

查看试题解析
22. 父亲节快到了，明明准备为爸爸煮四个大汤圆作早点：一个芝麻馅，一个水果馅，两个花生馅，四个汤圆除内部馅料不同外，其它一切均相同．

(1)、求爸爸吃到一个花生馅汤圆，一个芝麻馅汤圆的概率；

(2)、若给爸爸再增加一个花生馅的汤圆，则爸爸吃到一个花生馅汤圆，一个芝麻馅汤圆的可能性是否会增大？请说明理由．

查看试题解析
23. 为了解学生对于垃圾分类知识的掌握情况，某校组织了一次测试，为进一步了解测试的情况，从中抽取部分学生的成绩，分为A： $60 \leq x < 70$ ， B： $70 \leq x < 80$ ， C： $80 \leq x < 90$ ， D： $90 \leq x \leq 100$ 四个等级，并绘制了如下不完整的统计图．

(1)、已知条形统计图中有一处不符合题意，指出并改正；

(2)、为了使结果更准确，决定在本次抽取的人数基础上再增加m人，若增加后学生成绩的中位数所在等级与之前不相同，那么至少增加了几人？

(3)、从所抽取的学生中选一人，求选到的同学的成绩恰好为A等级的概率．

查看试题解析
24. 请用“一定”“很可能”“可能”“不太可能”“不可能”等语言来描述下列事件的可能性.

(1)、袋中有50个球，1个红的，49个白的，从中任取一球，取到红色的球；

(2)、掷一枚质地均匀的骰子，6点朝上；

(3)、100件产品中有2件次品，98件正品，从中任取一件，刚好是正品；

(4)、早晨太阳从东方升起；

(5)、小丽能跳100 m高.

查看试题解析

25. 文具店购进了20盒“

2 B

”铅笔，但在销售过程中，发现其中混入了若干“

H B

”铅笔．店员进行统计后，发现每盒铅笔中最多混入了2支“

H B

”铅笔，具体数据见下表：

混入“ $H B$ ”铅笔数	0	1	2
盒数	6	$m$	$n$

(1)、用等式写出

m

，

n

所满足的数量关系；

(2)、从20盒铅笔中任意选取1盒：

①“盒中没有混入‘ $H B$ ’铅笔”是事件；（填“必然”、“不可能”或“随机”）

②若“盒中混入1支‘ $H B$ ’铅笔”的概率为 $\frac{1}{4}$ ，求 $m$ 和 $n$ 的值．

查看试题解析

26. 在一个不透明的袋子里装有除数字外完全相同的3个小球，上面分别标有数字2，3，4．甲、乙两名同学做摸球游戏，游戏规则是：甲先从袋中随机摸出一个小球，乙再从袋中剩下的2个小球中随机摸出一个小球．若摸出的两个小球上的数字和为偶数，则甲胜，否则乙胜．

(1)、用列表法或画树状图法，求甲胜的概率；

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析