2022年浙教版数学九上复习阶梯训练:第2章 简单事件的概率 (提高训练)
试卷更新日期:2022-04-22 类型:复习试卷
一、单选题
-
1. 不透明的袋子中只有2个黑球和1个白球,这些球除颜色外其他无差别,随机从袋子中一次摸出2个球,下列事件为必然事件的是( )A、2个球都是黑球 B、2个球都是白球 C、2个球中有黑球 D、2个球中有白球2. 下列说法正确的是( )A、“山川异域,风月同天”是随机事件 B、买中奖率为1%的奖券100张,一定会中奖 C、“同旁内角互补”是必然事件 D、一枚硬币连抛100次,可能50次正面朝上3. 寒假期间,语文老师给学生布置了阅读任务,小国、小玲分别从《红楼梦》、《西游记》、《三国演义》三本名著中随机选择两本作为自己的阅读书目,则她俩选择的书目完全相同的概率是( )A、 B、 C、 D、4. 从﹣2, ,0,π, 这五个数中任意抽取一个,抽到无理数的概率为( )A、 B、 C、 D、5. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、12个 B、14个 C、16个 D、18个6. 做随机抛掷一枚纪念币的试验,得到的结果如下表所示:
抛掷次数m
500
1000
1500
2000
2500
3000
4000
5000
“正面向上”的次数n
265
512
793
1034
1306
1558
2083
2598
“正面向上”的频率
0.530
0.512
0.529
0.517
0.522
0.519
0.521
0.520
下面有3个推断:
①当抛掷次数是1000时,“正面向上”的频率是0.512,所以“正面向上”的概率是0.512;
②随着试验次数的增加,“正面向上”的频率总在0.520附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.520;
③若再次做随机抛掷该纪念币的实验,则当抛掷次数为3000时,出现“正面向上”的次数不一定是1558次.其中所有合理推断的序号是( )
A、② B、①③ C、②③ D、①②③7. 投掷一枚质地均匀的硬币m次,正面向上n次,下列表达正确的是( )A、的值一定是 B、的值一定不是 C、m越大,的值越接近 D、随着m的增加,的值会在附近摆动,呈现出一定的稳定性8. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.6左右,则袋子中红球的个数最有可能是( )A、5 B、8 C、12 D、159. 育种小组对某品种小麦发芽情况进行测试,在测试条件相同的情况下,得到如下数据:抽查小麦粒数
100
300
800
1000
2000
3000
发芽粒数
96
287
770
958
1923
a
则a的值最有可能是( )
A、2700 B、2780 C、2880 D、294010. 有两把不同的锁和四把钥匙,其中两把钥匙分别能打开这两把锁,其余两把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )A、 B、 C、 D、二、填空题
-
11. 标有数字1到9的相同大小的纸片9张,从中抽到一张素数纸片的可能性大小为 .12. 从标有数字1,2,3,4,5的五张卡片中,无放回地随机抽取两张,将抽取的卡片上的数字组成一个两位数,所组成的两位数的数字中为偶数的概率为 .13. 某篮球运动员进行定点投篮训练,其成绩如下表:
投篮次数
10
100
10000
投中次数
9
89
9012
则这名运动员定点投篮一次,投中的概率约是(精确到0.1)
14. 在一个不透明的布袋中,有黄色、白色的玻璃球共有20个,除颜色外,形状、大小、质地等完全相同,小刚每次换出一个球后放回通过多次摸球实验后发现摸到黄色球的频率稳定在40%,则布袋中白色球的个数很可能是.15. 为了估计水塘中的鱼数,养鱼者先从鱼塘中捕获50条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼.通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右,则鱼塘中估计有鱼条.16. 一个不透明的袋子中放有若干个红球,小亮往其中放入10个黑球,并采用以下实验方式估算其数量:每次摸出一个小球记录下颜色并放回,实验数据如下表:实验次数
100
200
300
400
摸出红球
78
161
238
321
则袋中原有红色小球的个数约为个.
三、综合题
-
17. 2022年冬奥会在我国北京和张家口举行,如图所示为冬奥会和冬残会的会徽“冬梦”“飞跃”,吉祥物“冰墩墩”“雪容融”,将四张正面分别印有以上4个图案的卡片(卡片的形状、大小、质地都相同)背面朝上洗匀.
 (1)、若从中随机抽取一张卡片,则抽取的卡片上的图案恰好为吉样物“冰墩墩”的概率是;(2)、若从中一次同时随机抽取两张卡片,请用画树状图或列表的方法,求抽取的两张卡片上的图案正好一张是会徽另一张是吉祥物的概率.18. 近几年,各式各样的共享经济模式在各个领域迅速普及应用,如图是某同学收集的四个共享经济领域的图标,将收集到的图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),背面朝上,洗匀放好.
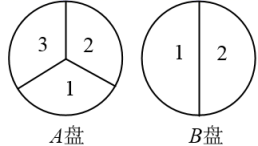
(1)、若从中随机抽取一张卡片,则抽取的卡片上的图案恰好为吉样物“冰墩墩”的概率是;(2)、若从中一次同时随机抽取两张卡片,请用画树状图或列表的方法,求抽取的两张卡片上的图案正好一张是会徽另一张是吉祥物的概率.18. 近几年,各式各样的共享经济模式在各个领域迅速普及应用,如图是某同学收集的四个共享经济领域的图标,将收集到的图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),背面朝上,洗匀放好.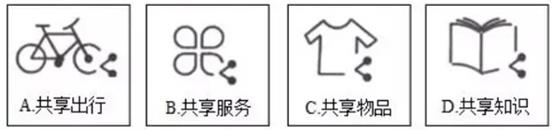 (1)、从中随机抽取一张,抽到的卡片恰好是“共享知识”的概率为;(2)、从中随机抽取一张,放回后洗匀,再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.19. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为 .(1)、请直接写出袋子中白球的个数.(2)、随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)20. 两个可以自由转动的转盘A、B都被分成3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,将指针所指两个区域内的数字相乘(若指针落在分割线上,则需重新转动转盘).
(1)、从中随机抽取一张,抽到的卡片恰好是“共享知识”的概率为;(2)、从中随机抽取一张,放回后洗匀,再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.19. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为 .(1)、请直接写出袋子中白球的个数.(2)、随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)20. 两个可以自由转动的转盘A、B都被分成3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,将指针所指两个区域内的数字相乘(若指针落在分割线上,则需重新转动转盘). (1)、试用列表或画树状图的方法,求数字之积为3的倍数的概率;(2)、小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.你认为这个游戏对双方公平吗?若公平,请说明理由;若不公平,请修改得分规定,使游戏对双方公平.21. 小明和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏: , 是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形.同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小明去观看,否则小亮去观看.
(1)、试用列表或画树状图的方法,求数字之积为3的倍数的概率;(2)、小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.你认为这个游戏对双方公平吗?若公平,请说明理由;若不公平,请修改得分规定,使游戏对双方公平.21. 小明和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游戏: , 是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形.同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小明去观看,否则小亮去观看. (1)、转动转盘一次,转出蓝色的概率是;(2)、这个游戏对双方公平吗?请说明理由(用树状图或列表法).22. 苗木种植不仅绿了家园,助力脱贫攻坚,也成为乡村增收致富的“绿色银行”.小王承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
(1)、转动转盘一次,转出蓝色的概率是;(2)、这个游戏对双方公平吗?请说明理由(用树状图或列表法).22. 苗木种植不仅绿了家园,助力脱贫攻坚,也成为乡村增收致富的“绿色银行”.小王承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:移植棵数(n)
成活数(m)
成活率()
移植棵数(n)
成活数(m)
成活率()
50
47
0.940
1500
1335
0.890
270
235
0.870
3500
3203
0.915
400
369
0.923
7000
6335
750
662
0.883
14000
12628
0.902
根据以上信息,回答下列问题:
(1)、当移植的棵数是7000时,表格记录成活数是 , 那么成活率x是(2)、随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是(3)、若小王移植10000棵这种树苗,则可能成活;(4)、若小王移植20000棵这种树苗,则一定成活18000棵.此结论符合题意吗?说明理由.23. 口袋里有除颜色外其它都相同的6个红球和4个白球.(1)、先从袋子里取出m()个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件A.①如果事件A是必然事件,请直接写出m的值.
②如果事件A是随机事件,请直接写出m的值.
(2)、先从袋子中取出m个白球,再放入m个一样的红球并摇匀,摸出一个球是红球的可能性大小是 , 求m的值.24. 现有两根长度分别为和的线段,同时,在一旁另有8根长度不等的线段,这些线段的长度分别与相应的卡片正面上标注的线段长一致.这8张卡片的背面完全相同,卡片正面上分别标注了.把这8张卡片背面朝上,从中随机抽取一张卡片,以卡片上标注的数据对应的线段作为第三条线段的长度,回答以下问题:(1)、“从中抽取的长度能够与和组成直角三角形”的概率为.(2)、求抽出的卡片上标注的数据对应的线段能够与和的线段组成等腰三角形的概率.(3)、小红和小艺打算以取出一张卡片上标注的数据对应的线段能够与和组成三角形的周长的奇偶性作为游戏规则.若三角形周长为奇数,则小红胜;若三角形周长为偶数,则小艺胜.请问游戏公平吗?若公平,请说明理由;若不公平,请重新设计一个公平的游戏规则.