2022年中考数学二轮专题复习-动态问题(移动)
试卷更新日期:2022-04-22 类型:二轮复习
一、单选题
-
1. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
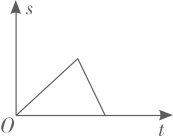 B、
B、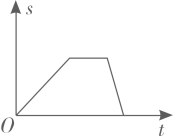 C、
C、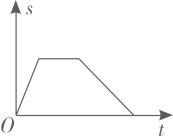 D、
D、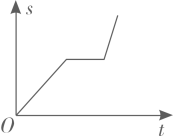 2. 均匀地向如图中的容器注水,最后把容器注满,在注水过程中,水面高度 随时间 的变化的图象是( )
2. 均匀地向如图中的容器注水,最后把容器注满,在注水过程中,水面高度 随时间 的变化的图象是( ) A、
A、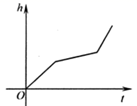 B、
B、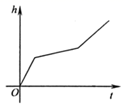 C、
C、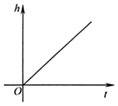 D、
D、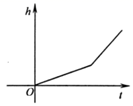 3. 小明在如图所示的扇形花坛 边沿O到A到B到O的路径散步,能表示小明离出发点 的距离 与时间 之间关系的大致图象是( )
3. 小明在如图所示的扇形花坛 边沿O到A到B到O的路径散步,能表示小明离出发点 的距离 与时间 之间关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
4. 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( ) A、
A、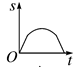 B、
B、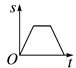 C、
C、 D、
D、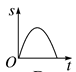 5. 一块含45°角的直角三角板和一把直尺按如图所示方式放置,直尺的一边EF与直角三角板的斜边AB位于同一直线上,DE>AB.开始时,点E与点A重合,直角三角板固定不动,然后将直尺沿AB方向平移,直到点F与点B重合时停止.设直尺平移的距离AE的长为x,边AC和BC被直尺覆盖部分的总长度为y,则y关于x的函数图象大致是( )
5. 一块含45°角的直角三角板和一把直尺按如图所示方式放置,直尺的一边EF与直角三角板的斜边AB位于同一直线上,DE>AB.开始时,点E与点A重合,直角三角板固定不动,然后将直尺沿AB方向平移,直到点F与点B重合时停止.设直尺平移的距离AE的长为x,边AC和BC被直尺覆盖部分的总长度为y,则y关于x的函数图象大致是( )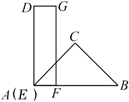 A、
A、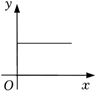 B、
B、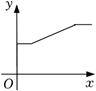 C、
C、 D、
D、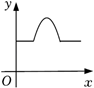 6. 如图1所示,△DEF中,∠DEF=90°,∠D=30°,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,图2是y与x之间函数的图象,则△ABD面积的最大值为( )
6. 如图1所示,△DEF中,∠DEF=90°,∠D=30°,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,图2是y与x之间函数的图象,则△ABD面积的最大值为( )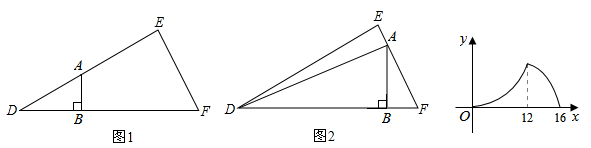 A、8 B、16 C、24 D、487. 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )
A、8 B、16 C、24 D、487. 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )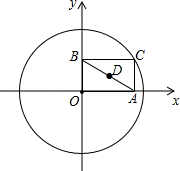 A、 B、 C、π D、2π8. 如图,的半径为6,将劣弧沿弦翻折,恰好经过圆心 , 点为优弧上的一个动点,则面积的最大值是( )
A、 B、 C、π D、2π8. 如图,的半径为6,将劣弧沿弦翻折,恰好经过圆心 , 点为优弧上的一个动点,则面积的最大值是( )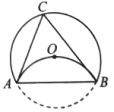 A、 B、 C、 D、9. 如图①,在▱ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y,y是x的函数,函数的图象如图②所示,则图②中的a值为( )
A、 B、 C、 D、9. 如图①,在▱ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y,y是x的函数,函数的图象如图②所示,则图②中的a值为( )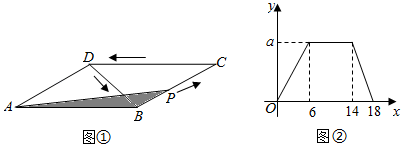 A、3 B、4 C、14 D、1810. 如图,平行四边形ABCD的边BC上有一动点E,连接DE,以DE为边作矩形DEGF且边FG过点A.在点E从点B移动到点C的过程中,矩形DEGF的面积( )
A、3 B、4 C、14 D、1810. 如图,平行四边形ABCD的边BC上有一动点E,连接DE,以DE为边作矩形DEGF且边FG过点A.在点E从点B移动到点C的过程中,矩形DEGF的面积( )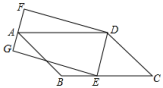 A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变11. 如图,已知在正方形ABCD中,厘米, , 点E在边AB上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动时间为t秒.若存在a与t的值,使与全等时,则t的值为( )
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变11. 如图,已知在正方形ABCD中,厘米, , 点E在边AB上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动时间为t秒.若存在a与t的值,使与全等时,则t的值为( )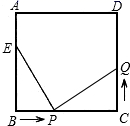 A、2 B、2或1.5 C、2.5 D、2.5或212. 如图,在△ABC中,AC=BC=8,∠BCA=60°,直线AD⊥BC于点D,E是AD上的一个动点,连接EC,将线段EC绕点C按逆时针方向旋转60°得到FC,连接DF,则在点E的运动过程中,DF的最小值是( )
A、2 B、2或1.5 C、2.5 D、2.5或212. 如图,在△ABC中,AC=BC=8,∠BCA=60°,直线AD⊥BC于点D,E是AD上的一个动点,连接EC,将线段EC绕点C按逆时针方向旋转60°得到FC,连接DF,则在点E的运动过程中,DF的最小值是( )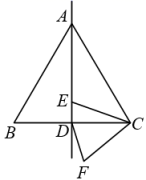 A、1 B、1.5 C、2 D、413. 如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为( )
A、1 B、1.5 C、2 D、413. 如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为( ) A、
A、 B、
B、 C、
C、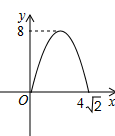 D、
D、 14. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )
14. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( ) A、
A、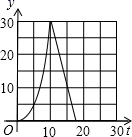 B、
B、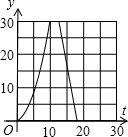 C、
C、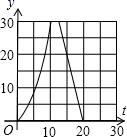 D、
D、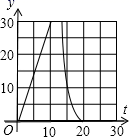 15. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )
15. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )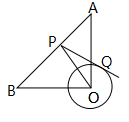 A、2 B、 C、1 D、216. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )
A、2 B、 C、1 D、216. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )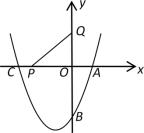 A、6 B、 C、 D、17. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )
A、6 B、 C、 D、17. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )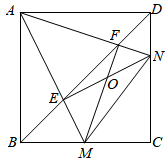 A、①②③ B、①②④ C、②③④ D、①②③④18. 如图,点A是函数y= 的图象上的点,点B,C的坐标分别为B(﹣ ,﹣ ),C( , ).试利用性质:“函数y= 的图象上任意一点A都满足|AB﹣AC|=2 ”求解下面问题:作∠BAC的角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
A、①②③ B、①②④ C、②③④ D、①②③④18. 如图,点A是函数y= 的图象上的点,点B,C的坐标分别为B(﹣ ,﹣ ),C( , ).试利用性质:“函数y= 的图象上任意一点A都满足|AB﹣AC|=2 ”求解下面问题:作∠BAC的角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )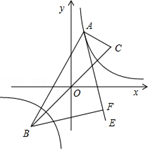 A、直线 B、抛物线 C、圆 D、反比例函数的曲线19. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( )
A、直线 B、抛物线 C、圆 D、反比例函数的曲线19. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( ) A、变大 B、变小 C、先变大再变小 D、保持不变20. 如图, 是等边三角形, ,点M从点C出发沿CB方向以 的速度匀速运动到点B , 同时点N从点C出发沿射线CA方向以 的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作 交AB于点P , 连接MN , NP , 作 关于直线MP对称的 ,设运动时间为ts , 与 重叠部分的面积为 ,则能表示S与t之间函数关系的大致图象为( )
A、变大 B、变小 C、先变大再变小 D、保持不变20. 如图, 是等边三角形, ,点M从点C出发沿CB方向以 的速度匀速运动到点B , 同时点N从点C出发沿射线CA方向以 的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作 交AB于点P , 连接MN , NP , 作 关于直线MP对称的 ,设运动时间为ts , 与 重叠部分的面积为 ,则能表示S与t之间函数关系的大致图象为( ) A、
A、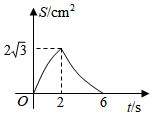 B、
B、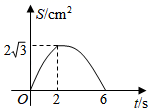 C、
C、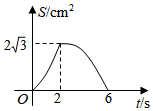 D、
D、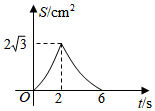
二、填空题
-
21. 如图,在 中, ,延长线段BC至点 使 ,连接AD.若点 是线段BC上一个动点,过点 作 交AB于点 ,连接AP,则当 的面积最大时,BP的长度为.
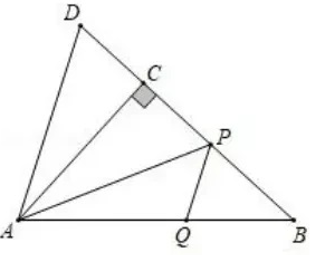 22. 如图,AB是半圆O的直径,半圆的半径为4,点C,D在半圆上, , 点P是OC上的一个动点,则的最小值为 .
22. 如图,AB是半圆O的直径,半圆的半径为4,点C,D在半圆上, , 点P是OC上的一个动点,则的最小值为 .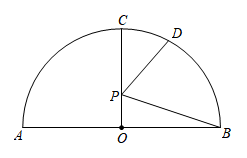 23. 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形处,则顶点O所经过的路线总长是 .
23. 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形处,则顶点O所经过的路线总长是 .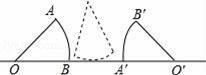 24. 如图,在中,AD为直径,弦于点H,连接OB.已知 , . 动点E从点O出发,在直径AD上沿路线以1cm/s的速度做匀速往返运动,运动时间为 . 当时,的值为 .
24. 如图,在中,AD为直径,弦于点H,连接OB.已知 , . 动点E从点O出发,在直径AD上沿路线以1cm/s的速度做匀速往返运动,运动时间为 . 当时,的值为 .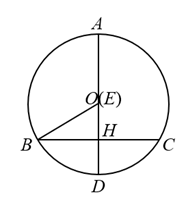 25. 如图,两根旗杆CA,DB相距20米,且CA⊥AB,DB⊥AB,某人从旗杆DB的底部B点沿BA走向旗杆CA底部A点.一段时间后到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角∠CMD=90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为每秒2米,则这个人从点B到点M所用时间是 秒.
25. 如图,两根旗杆CA,DB相距20米,且CA⊥AB,DB⊥AB,某人从旗杆DB的底部B点沿BA走向旗杆CA底部A点.一段时间后到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角∠CMD=90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为每秒2米,则这个人从点B到点M所用时间是 秒.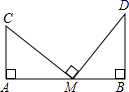 26. 如图,△ABC中AB=AC,A (0,8),C (6,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的倍,要使整个运动时间最少,则点D的坐标应为 .
26. 如图,△ABC中AB=AC,A (0,8),C (6,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的倍,要使整个运动时间最少,则点D的坐标应为 .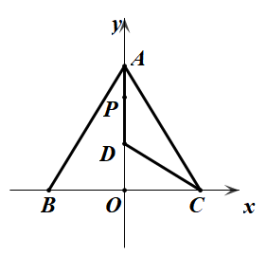 27. 如图,在平面直角坐标系中,二次函数 y=x2﹣2x+c 的图象与 x 轴交于 A、C 两点,与 y轴交于点 B(0,﹣3),若 P 是 x 轴上一动点,点 D(0,1)在 y 轴上,连接 PD,则 C 点的坐标是 , PD+PC 的最小值是 .
27. 如图,在平面直角坐标系中,二次函数 y=x2﹣2x+c 的图象与 x 轴交于 A、C 两点,与 y轴交于点 B(0,﹣3),若 P 是 x 轴上一动点,点 D(0,1)在 y 轴上,连接 PD,则 C 点的坐标是 , PD+PC 的最小值是 .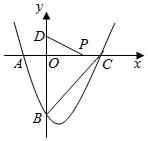 28. 如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .
28. 如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .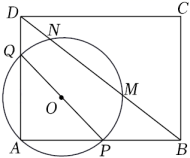 29. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .
29. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .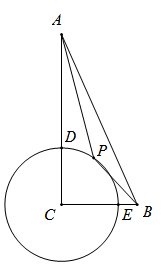 30. 如图,在平面直角坐标系中,矩形ABCD的顶点C在x轴正半轴上,顶点A在y轴正半轴上,顶点B与坐标原点O重合, , ,将矩形ABCD沿对角线AC裁开,将 沿CA方向平移得到 ,连接 , ,当四边形 为菱形时,点 的坐标为 .
30. 如图,在平面直角坐标系中,矩形ABCD的顶点C在x轴正半轴上,顶点A在y轴正半轴上,顶点B与坐标原点O重合, , ,将矩形ABCD沿对角线AC裁开,将 沿CA方向平移得到 ,连接 , ,当四边形 为菱形时,点 的坐标为 .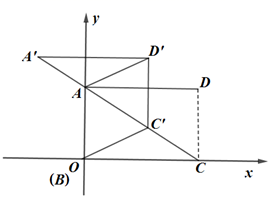
三、解答题
-
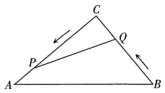
31. 如图,在△ACB中,AC=30cm,BC=25cm.动点P从点C出发,沿CA向终点A匀速运动,速度是2cm/s;同时,动点Q从点B出发,沿BC向终点C匀速运动,速度是1cm/s.当△CPQ与△CAB相似时,求运动的时间.
 32. 如图,在矩形ABCD中,AB=20cm,动点P从点A开始沿AB边以4cm/s的速度运动,动点Q从点C开始沿CD边以1cm/s的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设动点的运动时间为ts,则当t为何值时,四边形APQD是矩形?
32. 如图,在矩形ABCD中,AB=20cm,动点P从点A开始沿AB边以4cm/s的速度运动,动点Q从点C开始沿CD边以1cm/s的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设动点的运动时间为ts,则当t为何值时,四边形APQD是矩形?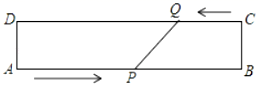 33. 如图,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.
33. 如图,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.(Ⅰ)求抛物线的解析式;
(Ⅱ)若抛物线交y轴于点C,在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)在抛物线第二象限的图象上是否存在一点P,使得△PBC的面积最大?若存在,请直接写出点P的坐标和△PBC面积的最大值;若不存在,请说明理由.
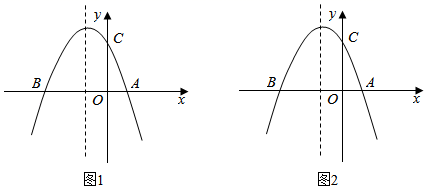 34. 如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?
34. 如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?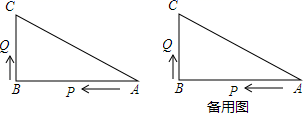 35. 如图,M、N是平行四边形ABCD对角线BD上两点.
35. 如图,M、N是平行四边形ABCD对角线BD上两点.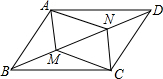
(1)、若BM=MN=DN,求证:四边形AMCN为平行四边形;
(2)、若M、N为对角线BD上的动点(均可与端点重合),设BD=12cm,点M由点B向点D匀速运动,速度为2(cm/s),同时点N由点D向点B匀速运动,速度为a(cm/s),运动时间为t(s).若要使四边形AMCN为平行四边形,求a的值及t的取值范围.36. 抛物线y=﹣x2+bx+c(b , c为常数)与x轴交于点(x1 , 0)和(x2 , 0),与y轴交于点A , 点E为抛物线顶点.(Ⅰ)当x1=﹣1,x2=3时,求点E , 点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.
37. 如如图,将一个直角三角形纸片AOB , 放置在平面直角坐标系中,已知点O(0,0),点B在y轴的正半轴上, OA=2,∠ABO=90°,∠AOB=30°.D , E两点同时从原点O出发,D点以每秒 个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,连接DE , 交OA于点F , 将△OEF沿直线DE折叠得到△O′EF , 设D , E两点的运动时间为t秒.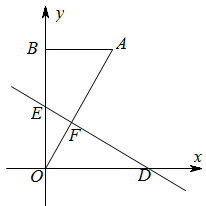 (1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,
(1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,①当折叠后 与 重叠部分的图形为三角形时,请写出 与 的函数关系式,并直接写出 的取值范围;
②当重叠部分面积最大时,把 绕点 旋转,得到 ,点 的对应点分别为 ,连接 ,求 面积的最大值(直接写出结果即可).
38. 在平面直角坐标系中,O为原点, 是等腰直角三角形, ,顶点 ,点B在第一象限,矩形 的顶点 ,点C在y轴的正半轴上,点D在第二象限,射线 经过点B.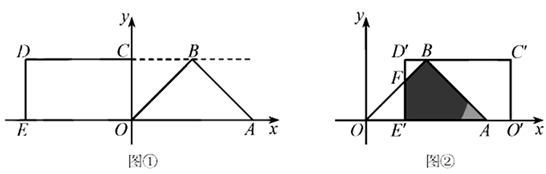
(Ⅰ)如图①,求点B的坐标;
(Ⅱ)将矩形 沿x轴向右平移,得到矩形 ,点O,C,D,E的对应点分别为 , , , ,设 ,矩形 与 重叠部分的面积为S.
①如图②,当点 在x轴正半轴上,且矩形 与 重叠部分为四边形时, 与 相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 时,求S的取值范围(直接写出结果即可).
39. 如图,在平面直角坐标系中,点A坐标为(0,3),点B坐标为(2,﹣1).
(Ⅰ)点C在第一象限内,AC x轴,将线段AB进行适当的平移得到线段DC , 点A的对应点为点D , 点B的对应点为点C , 连接AD , 若三角形ACD的面积为12,求线段AC的长;
(Ⅱ)在(Ⅰ)的条件下,连接OD , P为y轴上一个动点,若使三角形PAB的面积等于三角形AOD的面积,求此时点P的坐标.
40. 古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营A , B . 他总是先去A营,再到河边饮马,之后,再巡查B营.他时常想,怎么走,才能使他每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.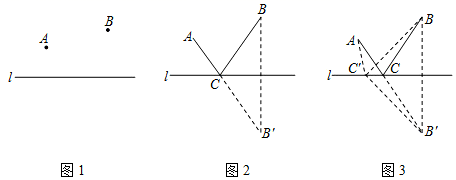
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C , 点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC , B′C′,
∵直线l是点B , B′的对称轴,点C , C′在l上,
∴CB= ▲ , C′B= ▲ ,
∴AC +CB=AC+CB′= ▲ .
在△AC′B′,
∵AB′<AC′+C′B′,
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A , B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A , C , B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
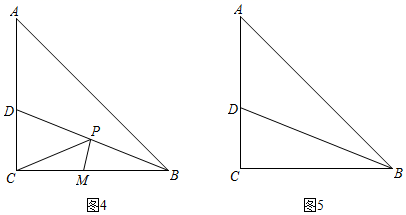
拓展应用:如图,等腰直角△ABC中,∠ACB = 90°,BD平分∠ABC交AC于D , 点P是BD上一个动点,点M是BC上一个动点,请在图5中画出PC + PM的值最小时P的位置.(可用三角尺)