2022年中考数学二轮专题复习-最值
试卷更新日期:2022-04-22 类型:二轮复习
一、单选题
-
1. 二次函数y=(x-3)2+1的最小值是( )A、3 B、-3 C、1 D、-12. 已知抛物线
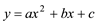 的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( ) A、最小值 -3 B、最大值-3 C、最小值2 D、最大值23. 二次函数 ( )的图象如图所示,则下列结论:①a<0;②函数有最小值;③ c>0,③ < 0,其中正确的个数是( )
的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( ) A、最小值 -3 B、最大值-3 C、最小值2 D、最大值23. 二次函数 ( )的图象如图所示,则下列结论:①a<0;②函数有最小值;③ c>0,③ < 0,其中正确的个数是( )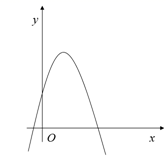 A、1个 B、2个 C、3个 D、4个4. 若抛物线y=(x+1)2+c与y轴相交于点(0,﹣5),则y的最小值为( )A、﹣6 B、6 C、﹣5 D、55. 二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
A、1个 B、2个 C、3个 D、4个4. 若抛物线y=(x+1)2+c与y轴相交于点(0,﹣5),则y的最小值为( )A、﹣6 B、6 C、﹣5 D、55. 二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:x
…
0
1
2
3
4
…
y
…
4
5
4
﹣4
﹣20
﹣45
…
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A、﹣45 B、﹣20 C、﹣4 D、06. 已知非负数a,b,c满足a+b=3且c﹣3a=﹣6,设y=a2+b+c的最大值为m,最小值为n,则m﹣n的值是( )A、16 B、15 C、9 D、77. 如图,在直角坐标系中, , , , 以A为位似中心且在点A同侧,把按相似比放大,放大后的图形记作 , 则的最小值是( )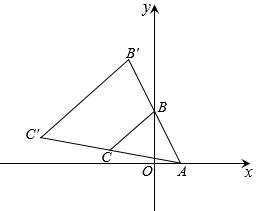 A、 B、 C、 D、38. 已知抛物线y=ax2﹣2ax+3不经过第四象限.当﹣1≤x≤2时,y的最大值与最小值的差是12,则a的值是( )A、﹣3 B、3 C、4 D、129. 如图,点E在正方形ABCD的AB边上,AE=3,BE=9,点P在BC上运动(不与B、C重合),PQ⊥EP,PQ交CD于点Q,则CQ的最大值是( )
A、 B、 C、 D、38. 已知抛物线y=ax2﹣2ax+3不经过第四象限.当﹣1≤x≤2时,y的最大值与最小值的差是12,则a的值是( )A、﹣3 B、3 C、4 D、129. 如图,点E在正方形ABCD的AB边上,AE=3,BE=9,点P在BC上运动(不与B、C重合),PQ⊥EP,PQ交CD于点Q,则CQ的最大值是( )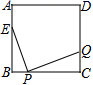 A、6 B、5 C、4 D、310. 如图,已知二次函数的图象(0≤x≤1+2 ).关于该函数在所给自变量取值范围内,下列说法正确的是( )
A、6 B、5 C、4 D、310. 如图,已知二次函数的图象(0≤x≤1+2 ).关于该函数在所给自变量取值范围内,下列说法正确的是( )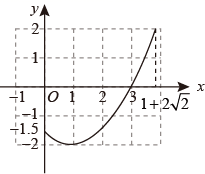 A、有最小值﹣2,无最大值 B、有最小值﹣2,有最大值﹣1.5 C、有最小值﹣2,有最大值2 D、有最小值﹣1.5,有最大值211. 如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(﹣2,﹣3),(1,﹣3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )
A、有最小值﹣2,无最大值 B、有最小值﹣2,有最大值﹣1.5 C、有最小值﹣2,有最大值2 D、有最小值﹣1.5,有最大值211. 如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(﹣2,﹣3),(1,﹣3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )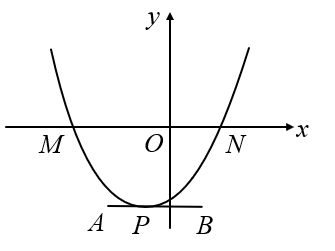 A、﹣1 B、﹣3 C、﹣5 D、﹣712. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:①当x>0时,y>0;②若a=-1,则b=5;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2, 则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为 .其中正确的有( )个
A、﹣1 B、﹣3 C、﹣5 D、﹣712. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:①当x>0时,y>0;②若a=-1,则b=5;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2, 则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为 .其中正确的有( )个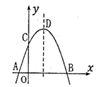 A、0 B、1 C、2 D、313. 如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为( )
A、0 B、1 C、2 D、313. 如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为( )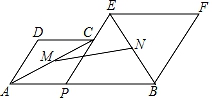 A、 B、 C、4 D、314. 如图,抛物线y1=a(x+1)2﹣5与抛物线y2=﹣a(x﹣1)2+5(a≠0)交于点A(2,4),B(m , ﹣4),若无论x取任何值,y总取y1 , y2中的最小值,则y的最大值是( )
A、 B、 C、4 D、314. 如图,抛物线y1=a(x+1)2﹣5与抛物线y2=﹣a(x﹣1)2+5(a≠0)交于点A(2,4),B(m , ﹣4),若无论x取任何值,y总取y1 , y2中的最小值,则y的最大值是( )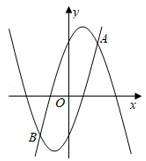 A、4 B、5 C、2 D、115. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a , b , c , 记 ,则其面积 .这个公式也被称为海伦-秦九韶公式.若 ,则此三角形面积的最大值为( )A、 B、4 C、 D、516. 如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。则下列结论不正确的是( )
A、4 B、5 C、2 D、115. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a , b , c , 记 ,则其面积 .这个公式也被称为海伦-秦九韶公式.若 ,则此三角形面积的最大值为( )A、 B、4 C、 D、516. 如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。则下列结论不正确的是( ) A、当△AHG的面积等于矩形面积时,HE的长为5cm B、当HE的长为6cm时,剪下的矩形的边HG是HE的2倍 C、当矩形的边HG是HE的2倍时,矩形面积最大 D、当矩形的面积最大时,HG的长是10cm17. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
A、当△AHG的面积等于矩形面积时,HE的长为5cm B、当HE的长为6cm时,剪下的矩形的边HG是HE的2倍 C、当矩形的边HG是HE的2倍时,矩形面积最大 D、当矩形的面积最大时,HG的长是10cm17. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )
A、①②③ B、③④ C、①②④ D、①②③④18. 关于二次函数y=x2﹣4m x+3 (m是常数),有以下说法:①不管m是什么实数,该函数图象的顶点一定在函数y=﹣x2 +3的图象上;②若该函数图象与x轴相交于点(a,0), (b, 0) (a<b),并且方程x2﹣4m x+3﹣t=0 (t是常数)的根是x1=c,x2=d (c<d), 则一定有c<a<b < d; ③当-1≤x≤0时,若有最小值2,则m=﹣ 。 其中正确的说法是( )
A、①② B、②③ C、①③ D、①②③19. 新定义:若关于x的一元二次方程:a1(x-m)2+n=0与a2(x-m)2+n=0,称为“同族二次方程”如2(x-3)2+4=0与3(x-3)2+4=0是“同族二次方程”现有关于x的一元二次方程2(x-1)2+1=0与(a+2)x2+(b-4)x+8=0是“同族二次方程”,那么代数式ax2+bx+2018能取的最小值是( )A、2011 B、2013 C、2018 D、202320. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )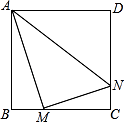 A、8 B、4 C、10 D、8
A、8 B、4 C、10 D、8二、填空题
-
21. 若把函数y=x的图象用E(x,x)记,函数y=2x+1的图象用E(x,2x+1)记,……则E(x, )图象上的最低点是.22. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为.23. 如图,在平面直角坐标系 中,点P的坐标为 , , 的半径为1,点Q在 上,连接 ,若 与 相切.则线段 的最小值为.
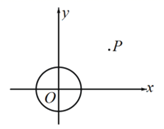 24. 飞机着陆后滑行的距离S(单位:米)与滑行的时间t(单位:秒)的函数关系式是 ,飞机着陆滑行的最远距离是米.25. 如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,设BE=x,则CF=(用x表示);则GM的最小值为.
24. 飞机着陆后滑行的距离S(单位:米)与滑行的时间t(单位:秒)的函数关系式是 ,飞机着陆滑行的最远距离是米.25. 如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,设BE=x,则CF=(用x表示);则GM的最小值为.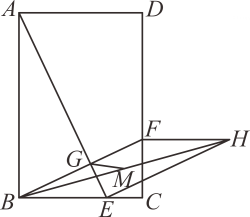 26. 如图,直线y=﹣x+m与双曲线y=﹣ 相交于A,B两点BC∥x轴,AC∥y轴,则△ABC面积的最小值为.
26. 如图,直线y=﹣x+m与双曲线y=﹣ 相交于A,B两点BC∥x轴,AC∥y轴,则△ABC面积的最小值为.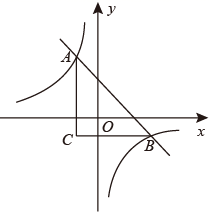 27. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
27. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)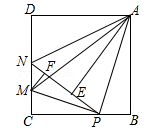
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为;
⑤当△ABP≌△ADN时,BP=.
28. 如图,已知 ,在x轴上取 两点,使 ,把线段 交点A沿逆时针方向旋转 ,得线段 ,把线段 绕点B沿顺时针方向旋转 ,得线段 ,当 两点之间的距离最小时,点C的坐标为.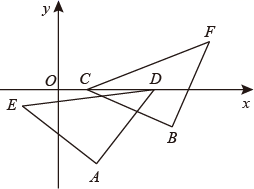 29. 如图,在△ABC中,∠ACB=120°,AC=8,BC=4,点P是线段AC上的一个动点,连接BP,Q为线段BP中点,将线段PQ绕点P逆时针旋转120°得到线段PD,连接AD,则线段AD的最小值是.
29. 如图,在△ABC中,∠ACB=120°,AC=8,BC=4,点P是线段AC上的一个动点,连接BP,Q为线段BP中点,将线段PQ绕点P逆时针旋转120°得到线段PD,连接AD,则线段AD的最小值是.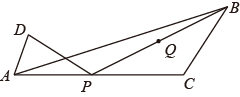 30. 我们定义一种新函数:形如 ( ,且 )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为 , 和 ;②图象具有对称性,对称轴是直线 ;③当 或 时,函数值 随 值的增大而增大;④当 或 时,函数的最小值是0;⑤当 时,函数的最大值是4.其中正确的结论有 . (填序号)
30. 我们定义一种新函数:形如 ( ,且 )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为 , 和 ;②图象具有对称性,对称轴是直线 ;③当 或 时,函数值 随 值的增大而增大;④当 或 时,函数的最小值是0;⑤当 时,函数的最大值是4.其中正确的结论有 . (填序号)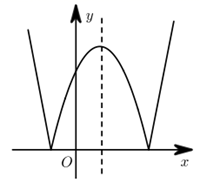
三、解答题
-
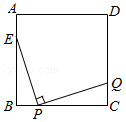
31. 如图,正方形ABCD中,AB=12,AE= AB , 点P在BC上运动(不与B , C重合),过点P作PQ⊥EP , 交CD于点Q , 求在点P运动的过程中,BP多长时,CQ有最大值,并求出最大值.
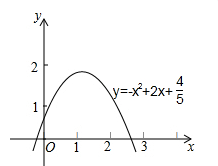
 32. 根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少?
32. 根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少?
 33. 函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)、分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x-1)2+1的最大值和最小值.
33. 函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)、分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x-1)2+1的最大值和最小值.
(2)、对于二次函数y=2(x-m)2+m-2,当2≤x≤4时有最小值为1,求m的值.
34. 已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM (1)、画出△A1PM(2)、设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.35. 由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)、完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
(1)、画出△A1PM(2)、设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.35. 由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)、完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;售价(元/台)
月销售量(台)
400
200
▲
250
x
▲
(2)、当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?36. 甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度.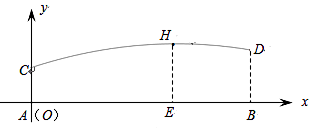 37. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D.
37. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.38. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
(1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.38. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
39. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批淡水鱼放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知: 与 的函数关系为 ; 与 的函数关系如图所示.
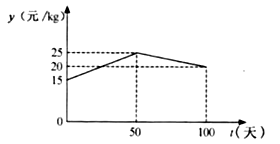
①分别求出当 和 时, 与 的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为 元,求当 为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
40. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)、根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ② ③(2)、请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?(3)、已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值