新疆维吾尔自治区2022届高三普通高考理数第二次适应性检测试卷
试卷更新日期:2022-04-22 类型:高考模拟
一、单选题
-
1. 设是复数的共轭复数,若复数在复平面内对应的点为 , 则( )A、2+4i B、2-4i C、-2-4i D、-2+4i2. 已知集合 , , 全集 , 则( )A、A B、B C、 D、Z3. 已知命题P: , ;命题: , , 下列命题中为假命题的是( )A、 B、 C、 D、4. 我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来研究函数图象的特征.我们从这个商标
 中抽象出一个函数的图象如图,其对应的函数解析式可能是( )
中抽象出一个函数的图象如图,其对应的函数解析式可能是( )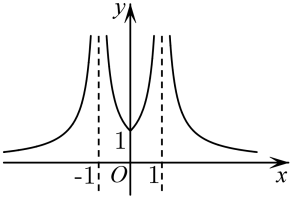 A、 B、 C、 D、5. 设是直线, , 是两个不同的平面,则下列命题正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则6. 已知数列的各项为互异正数,且其倒数构成公差为3的等差数列,则( )A、 B、 C、3 D、67. 某几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为( )
A、 B、 C、 D、5. 设是直线, , 是两个不同的平面,则下列命题正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则6. 已知数列的各项为互异正数,且其倒数构成公差为3的等差数列,则( )A、 B、 C、3 D、67. 某几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为( )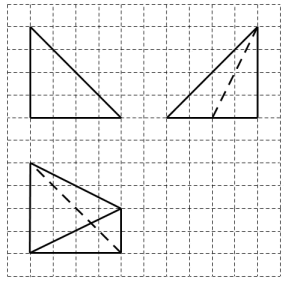 A、 B、 C、 D、8. 把1,2,3,4,5这五个数随机排成一列,组成一个数列,要求该数列恰好先减后增,则这样的数列有( )A、13个 B、14个 C、15个 D、16个9. 某数学兴趣小组要测量校园内国旗杆的高度,测量的同学在地面选择了 , 两个观测点,且A,B,C三点在同一直线上,如图所示.在处测得国旗杆顶端D的仰角为 , 在处测得国旗杆顶端D的仰角为.若 , 则国旗杆CD的高度为( )
A、 B、 C、 D、8. 把1,2,3,4,5这五个数随机排成一列,组成一个数列,要求该数列恰好先减后增,则这样的数列有( )A、13个 B、14个 C、15个 D、16个9. 某数学兴趣小组要测量校园内国旗杆的高度,测量的同学在地面选择了 , 两个观测点,且A,B,C三点在同一直线上,如图所示.在处测得国旗杆顶端D的仰角为 , 在处测得国旗杆顶端D的仰角为.若 , 则国旗杆CD的高度为( )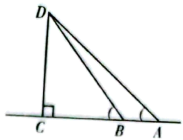 A、 B、 C、 D、10. 若函数有两个零点,则的取值范围为( )A、 B、 C、 D、11. 已知点是双曲线上的动点, , 分别为其左,右焦点,为坐标原点.则的最大值是( )A、7 B、6 C、5 D、412. 实数 , , 分别满足 , , , 则 , , 的大小关系为( )A、 B、 C、 D、
A、 B、 C、 D、10. 若函数有两个零点,则的取值范围为( )A、 B、 C、 D、11. 已知点是双曲线上的动点, , 分别为其左,右焦点,为坐标原点.则的最大值是( )A、7 B、6 C、5 D、412. 实数 , , 分别满足 , , , 则 , , 的大小关系为( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , , 若 , 则.14. 若为抛物线的焦点,为抛物线上一点,为抛物线准线与坐标轴的交点,且 , 的面积为 , 则抛物线的方程为.15. 在正项等比数列中, , , 则满足的最小正整数的值为.16. 已知正方体的棱长为1,、分别为棱、的中点,为棱上的动点,为线段的中点.则下列结论中正确序号为.
①;②平面;③的余弦值的取值范围是;④△周长的最小值为
三、解答题
-
17. 设的内角 , , 所对边的长分别为 , , , 且(1)、求角的大小;(2)、若 , , 为的中点,求的长.18. 如图,在三棱柱中,平面平面 , 是正三角形,是的中点. , 直线与平面所成的角为.
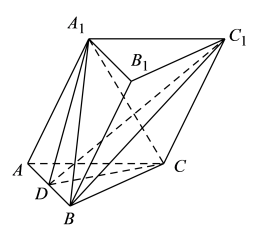 (1)、求证:平面;(2)、求二面角的正弦值.19. 2021年8月8日是我国第13个“全民健身日”,社会上参与全民健身活动的人越来越多,小明也有大量好友参与了“健步团”,他随机选取了其中的40人,记录了他们某一天的走路步数,并将数据整理如下:
(1)、求证:平面;(2)、求二面角的正弦值.19. 2021年8月8日是我国第13个“全民健身日”,社会上参与全民健身活动的人越来越多,小明也有大量好友参与了“健步团”,他随机选取了其中的40人,记录了他们某一天的走路步数,并将数据整理如下:步量
性别
5001~6000
6001~7000
7001~8000
8001~9000
>9000
男
1
2
3
6
8
女
0
2
10
6
2
附:参考公式.
临界值表:
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
(1)、若在小明该日走路不超过7000步的好友中任选2人,求至少有1名男性的概率;(2)、如果每人一天的走路步数超过8000步就会被系统评定为“健步型”,否则为“良好型”,根据题意完成下面的列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关健步型
良好型
总计
男
女
总计
20. 设函数 , 其中(1)、当时,讨论单调性;(2)、证明:有唯一极值点 , 且.