四川省达州市2022届高三理数第二次诊断性测试试卷
试卷更新日期:2022-04-22 类型:高考模拟
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 复数z满足 , 则( )A、1 B、 C、 D、23. 已知随机变量 , 若 , 则( )A、0.18 B、0.36 C、0.32 D、0.164. 过抛物线焦点F的直线与圆相切于点P,则( )A、3 B、 C、4 D、5. 将函数图象上所有点向左平移个单位长度,得到函数的图象,若是奇函数,则a的最小值是( )A、 B、 C、 D、6. 设是两条不同的直线,是两个不同的平面,则下列为假命题的是( )A、若 , , 则 B、若 , , , 则 C、若 , , 则 D、若 , , , 则7. 1707年发现了指数与对数的互逆关系:当 , 时,等价于.若 , , , 则的值约为( )A、3.219 B、2.3256 C、2.5259 D、2.73168. 已知单调递增数列满足 , 则实数m的取值范围是( )A、 B、 C、 D、9. 函数的部分图象大致为( )A、
 B、
B、 C、
C、 D、
D、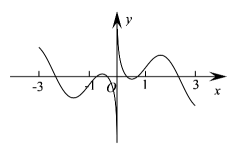 10. 已知 , , 则( )A、 B、 C、 D、11. 函数的最小值为 , 则直线与曲线的交点个数为( )A、1 B、2 C、3 D、412. 设 , 则下列说法正确的是( )A、值域为 B、在上单调递增 C、在上单调递减 D、
10. 已知 , , 则( )A、 B、 C、 D、11. 函数的最小值为 , 则直线与曲线的交点个数为( )A、1 B、2 C、3 D、412. 设 , 则下列说法正确的是( )A、值域为 B、在上单调递增 C、在上单调递减 D、二、填空题
-
13. 的展开式中 的系数为.14. 函数满足:①定义域为R,② , ③.请写出满足上述条件的一个函数 , .15. 如图,在梯形中, , , , , , 则.
 16. 在棱长为的正方体中,分别为的中点,为正方体棱上一动点.下列说法中所有正确的序号是
16. 在棱长为的正方体中,分别为的中点,为正方体棱上一动点.下列说法中所有正确的序号是①在AB上运动时,存在某个位置,使得与所成角为;
②在AB上运动时,MG与所成角的最大正弦值为;
③在上运动且时,过三点的平面截正方体所得多边形的周长为;
④在上运动时(不与重合),若点在同一球面上,则该球表面积最大值为.
三、解答题
-
17. 为配合创建文明城市,某市交警支队全面启动路口秩序综合治理,重点整治机动车不礼让行人的行为.经过一段时间的治理,从市交警队数据库中调取了10个路口的车辆违章数据,根据这10个路口的违章车次的数量绘制如下的频率分布直方图,数据中凡违章车次超过40次的路口设为“重点关注路口”.
 (1)、根据直方图估计这10个路口的违章车次的平均数;(2)、现从支队派遣3位交警去违章车次在的路口执勤,每人选择一个路口,每个路口至多1人,设去“重点关注路口”的交警人数为X,求X的分布列及数学期望.18. 已知数列满足 , , 为的前n项和.(1)、求的通项公式;(2)、设 , 数列的前n项和满足对一切正奇数n恒成立,求实数m的取值范围.19. 在四棱锥中,四边形为平行四边形,是等边三角形,.
(1)、根据直方图估计这10个路口的违章车次的平均数;(2)、现从支队派遣3位交警去违章车次在的路口执勤,每人选择一个路口,每个路口至多1人,设去“重点关注路口”的交警人数为X,求X的分布列及数学期望.18. 已知数列满足 , , 为的前n项和.(1)、求的通项公式;(2)、设 , 数列的前n项和满足对一切正奇数n恒成立,求实数m的取值范围.19. 在四棱锥中,四边形为平行四边形,是等边三角形,. (1)、证明:;(2)、若 , , 求二面角的正弦值.20. 已知椭圆的离心率为 , 过的右顶点的直线与的另一交点为.当为的上顶点时,原点到的距离为.(1)、求的标准方程;(2)、过A与垂直的直线交抛物线于两点,求面积的最小值.
(1)、证明:;(2)、若 , , 求二面角的正弦值.20. 已知椭圆的离心率为 , 过的右顶点的直线与的另一交点为.当为的上顶点时,原点到的距离为.(1)、求的标准方程;(2)、过A与垂直的直线交抛物线于两点,求面积的最小值.